
Question and Answers Forum
Question Number 36413 by abdo.msup.com last updated on 01/Jun/18
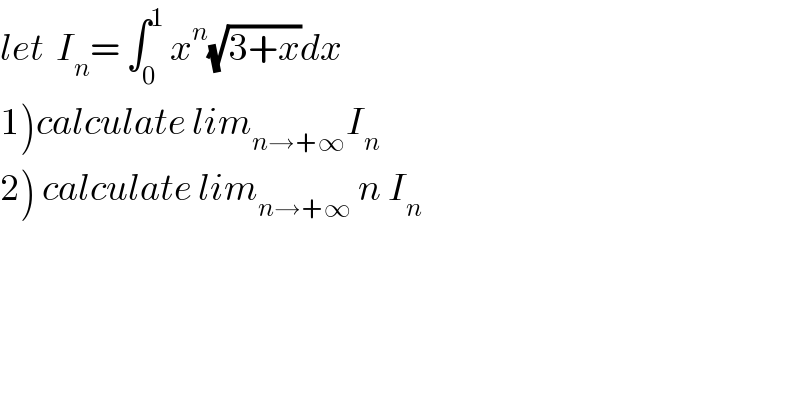
Commented by abdo.msup.com last updated on 04/Jun/18
![1) we have 0≤x≤1 ⇒ 3≤3+x≤4 ⇒ (√3) ≤(√(3+x))≤2 ⇒ ∫_0 ^1 (√3) x^n dx≤I_n ≤∫_0 ^1 2x^n dx ⇒ ((√3)/(n+1)) ≤ I_n ≤ (2/(n+1)) →_(n→+∞) 0 so lim_(n→+∞) I_n =0 2) by parts I_n =[ (1/(n+1))x^(n+1) (√(3+x))]_0 ^1 −∫_0 ^1 (x^(n+1) /(n+1)) (1/(2(√(3+x))))dx =(2/(n+1)) −(1/(2(n+1))) ∫_0 ^1 (x^(n+1) /(√(3+x)))dx⇒ nI_n = ((2n)/(n+1)) −(n/(2n+2)) ∫_0 ^1 (x^(n+1) /(√(3+x)))dx but (√3)≤(√(3+x))≤2 ⇒ (1/2) ≤ (1/(√(3+x)))≤(√3) ⇒ (x^(n+1) /2) ≤ (x^(n+1) /(√(3+x))) ≤ (√3) x^(n+1) ⇒ ∫_0 ^1 (x^(n+1) /2)dx≤ ∫_0 ^1 (x^(n+1) /(√(3+x)))dx≤ (√3)∫_0 ^1 x^(n+1) dx ⇒ (1/(2(n+2))) ≤ ∫_0 ^1 (x^(n+1) /(√(3+x)))dx≤ ((√3)/(n+1)) so lim_(n→+∞) ∫_0 ^1 (x^(n+1) /(√(3+x)))dx =0 ⇒ lim n I_n =2 (n→+∞)](Q36732.png)
| ||
Question and Answers Forum | ||
Question Number 36413 by abdo.msup.com last updated on 01/Jun/18 | ||
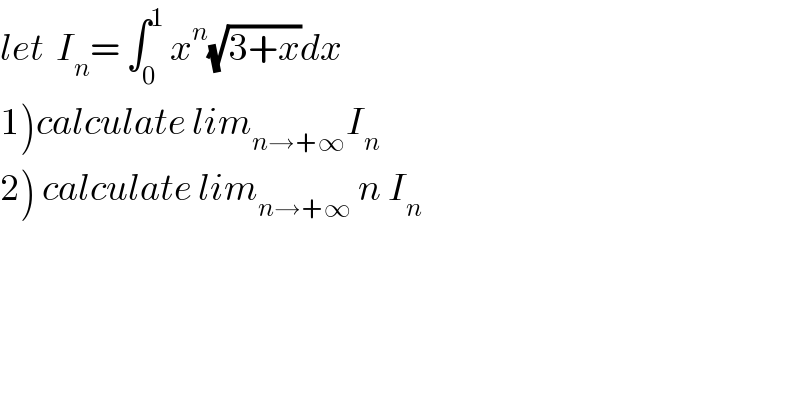 | ||
Commented by abdo.msup.com last updated on 04/Jun/18 | ||
![1) we have 0≤x≤1 ⇒ 3≤3+x≤4 ⇒ (√3) ≤(√(3+x))≤2 ⇒ ∫_0 ^1 (√3) x^n dx≤I_n ≤∫_0 ^1 2x^n dx ⇒ ((√3)/(n+1)) ≤ I_n ≤ (2/(n+1)) →_(n→+∞) 0 so lim_(n→+∞) I_n =0 2) by parts I_n =[ (1/(n+1))x^(n+1) (√(3+x))]_0 ^1 −∫_0 ^1 (x^(n+1) /(n+1)) (1/(2(√(3+x))))dx =(2/(n+1)) −(1/(2(n+1))) ∫_0 ^1 (x^(n+1) /(√(3+x)))dx⇒ nI_n = ((2n)/(n+1)) −(n/(2n+2)) ∫_0 ^1 (x^(n+1) /(√(3+x)))dx but (√3)≤(√(3+x))≤2 ⇒ (1/2) ≤ (1/(√(3+x)))≤(√3) ⇒ (x^(n+1) /2) ≤ (x^(n+1) /(√(3+x))) ≤ (√3) x^(n+1) ⇒ ∫_0 ^1 (x^(n+1) /2)dx≤ ∫_0 ^1 (x^(n+1) /(√(3+x)))dx≤ (√3)∫_0 ^1 x^(n+1) dx ⇒ (1/(2(n+2))) ≤ ∫_0 ^1 (x^(n+1) /(√(3+x)))dx≤ ((√3)/(n+1)) so lim_(n→+∞) ∫_0 ^1 (x^(n+1) /(√(3+x)))dx =0 ⇒ lim n I_n =2 (n→+∞)](Q36732.png) | ||