
Question and Answers Forum
Question Number 92839 by i jagooll last updated on 09/May/20
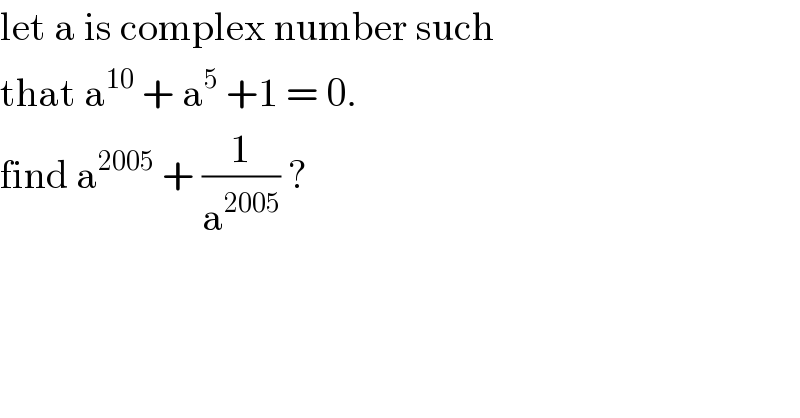
Answered by john santu last updated on 09/May/20
![set a^5 = w ⇒ w^2 +w+1 = 0 w^2 +w+1 = ((w^3 −1)/(w−1)) = 0 ⇒a^(10) +a^5 +1 = ((a^(15) −1)/(a^5 −1)) = 0 a^(15) = 1 ⇒ since 2005 = 133×15+10 a^(2005) = (a^(15) )^(133) ×a^(10) = 1×a^(10) = a^(10) then a^(2005) +(1/a^(2005) ) = a^(10) +(1/a^(10) ) = a^(10) +((a^(15) )/a^(10) ) = a^(10) +a^5 = −1 [ a^(10) +a^5 +1 = 0 ]](Q92841.png)
Commented by i jagooll last updated on 09/May/20

Commented by peter frank last updated on 09/May/20

| ||
Question and Answers Forum | ||
Question Number 92839 by i jagooll last updated on 09/May/20 | ||
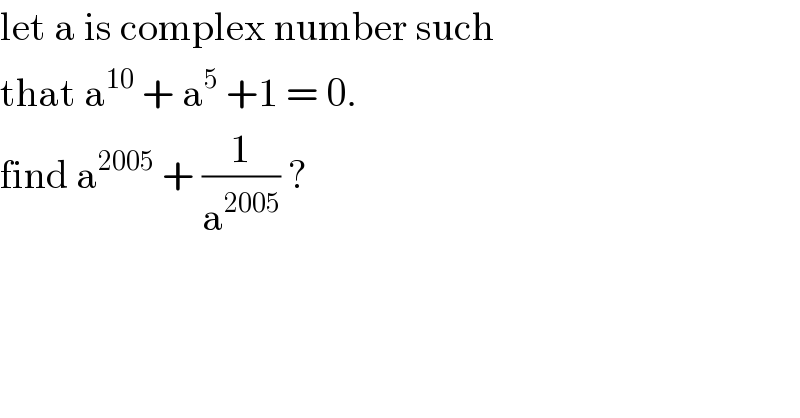 | ||
Answered by john santu last updated on 09/May/20 | ||
![set a^5 = w ⇒ w^2 +w+1 = 0 w^2 +w+1 = ((w^3 −1)/(w−1)) = 0 ⇒a^(10) +a^5 +1 = ((a^(15) −1)/(a^5 −1)) = 0 a^(15) = 1 ⇒ since 2005 = 133×15+10 a^(2005) = (a^(15) )^(133) ×a^(10) = 1×a^(10) = a^(10) then a^(2005) +(1/a^(2005) ) = a^(10) +(1/a^(10) ) = a^(10) +((a^(15) )/a^(10) ) = a^(10) +a^5 = −1 [ a^(10) +a^5 +1 = 0 ]](Q92841.png) | ||
| ||
Commented by i jagooll last updated on 09/May/20 | ||
 | ||
Commented by peter frank last updated on 09/May/20 | ||
 | ||