
Question and Answers Forum
Question Number 40138 by maxmathsup by imad last updated on 16/Jul/18
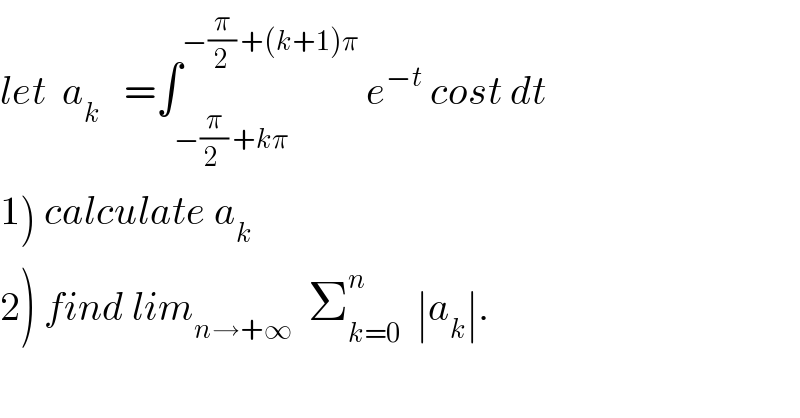
Commented by maxmathsup by imad last updated on 20/Jul/18
![1) we have a_k =_(t=kπ +x) ∫_(−(π/2)) ^(π/2) e^(−(kπ+x)) cos(x+kπ)dx = ∫_(−(π/2)) ^(π/2) e^(−kπ) e^(−x) (−1)^k cosx dx =(−1)^k e^(−kπ) ∫_(−(π/2)) ^(π/2) e^(−x) cosxdx but ∫_(−(π/2)) ^(π/2) e^(−x) cosx dx=Re( ∫_(−(π/2)) ^(π/2) e^(−x) e^(ix) ) =Re( ∫_(−(π/2)) ^(π/2) e^((−1+i)x) dx) =Re( [(1/(−1+i)) e^((−1+i)x) ]_(−(π/2)) ^(π/2) =Re( (1/(−1+i))( e^((−1+i)(π/2)) −e^(−(−1+i)(π/2)) )) =Re{ ((−1)/(1−i))( e^(−(π/2)) i + e^(π/2) i}=Re { ((−i)/(1−i))( e^(π/2) +e^(−(π/2)) )} =Re( ((−i(1+i))/2)( e^(π/2) +e^(−(π/2)) ))= Re( ((−i+1)/2)(e^(π/2) +e^(−(π/2)) )) =((e^(π/2) +e^(−(π/2)) )/2) =ch((π/2)) ⇒ a_k =(−1)^k e^(−kπ) ch((π/2)) .](Q40361.png)
Commented by maxmathsup by imad last updated on 20/Jul/18

| ||
Question and Answers Forum | ||
Question Number 40138 by maxmathsup by imad last updated on 16/Jul/18 | ||
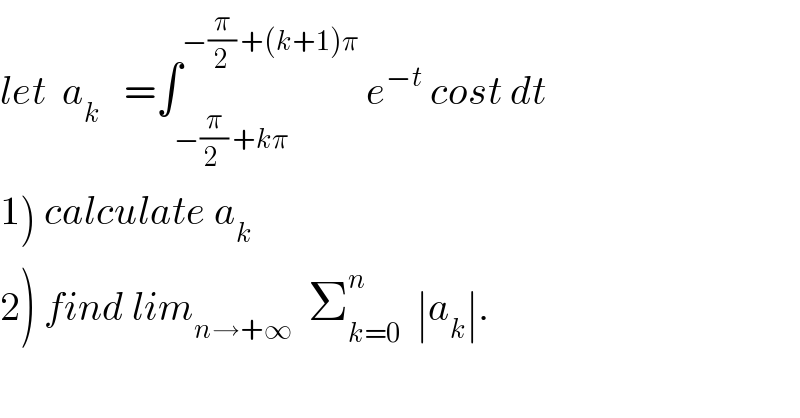 | ||
Commented by maxmathsup by imad last updated on 20/Jul/18 | ||
![1) we have a_k =_(t=kπ +x) ∫_(−(π/2)) ^(π/2) e^(−(kπ+x)) cos(x+kπ)dx = ∫_(−(π/2)) ^(π/2) e^(−kπ) e^(−x) (−1)^k cosx dx =(−1)^k e^(−kπ) ∫_(−(π/2)) ^(π/2) e^(−x) cosxdx but ∫_(−(π/2)) ^(π/2) e^(−x) cosx dx=Re( ∫_(−(π/2)) ^(π/2) e^(−x) e^(ix) ) =Re( ∫_(−(π/2)) ^(π/2) e^((−1+i)x) dx) =Re( [(1/(−1+i)) e^((−1+i)x) ]_(−(π/2)) ^(π/2) =Re( (1/(−1+i))( e^((−1+i)(π/2)) −e^(−(−1+i)(π/2)) )) =Re{ ((−1)/(1−i))( e^(−(π/2)) i + e^(π/2) i}=Re { ((−i)/(1−i))( e^(π/2) +e^(−(π/2)) )} =Re( ((−i(1+i))/2)( e^(π/2) +e^(−(π/2)) ))= Re( ((−i+1)/2)(e^(π/2) +e^(−(π/2)) )) =((e^(π/2) +e^(−(π/2)) )/2) =ch((π/2)) ⇒ a_k =(−1)^k e^(−kπ) ch((π/2)) .](Q40361.png) | ||
Commented by maxmathsup by imad last updated on 20/Jul/18 | ||
 | ||