
Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 146902 by mathmax by abdo last updated on 16/Jul/21
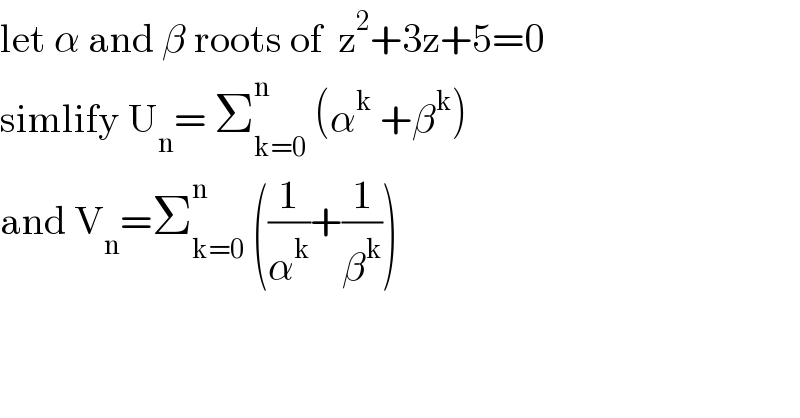
Answered by ArielVyny last updated on 18/Jul/21
![z^2 +3z+5=0→(z+(3/2))^2 −(9/4)+((20)/4)=0 (z+(3/2))^2 +((11)/4)=0 (z+(3/2)−i((√(11))/2))(z+(3/2)+i((√(11))/2))=0 then α=−(3/2)+i((√(11))/2) and β=−(3/2)−i((√(11))/2) U_n =Σ_(k=0) ^n (α^k +β^k ) ∣α∣=∣−(3/2)+i((√(11))/2)∣=(√((−(3/2))^2 +(((√(11))/2))^2 )) ∣α∣=(√((9/4)+((11)/4)))=((√(20))/2) α=((√(20))/2)(−((3/2)/((√(20))/2))+i(((√(11))/2)/((√(20))/2)))=((√(20))/2)(−(3/( (√(20))))+i((√(11))/( (√(20))))) α=((√(20))/2)e^(iθ) tel que { ((cosθ=−(3/( (√(20)))))),((sinθ=(√((11)/(20))))) :} β=((√(20))/2)e^(−iθ) U_n =Σ_(k=0) ^n [(((√(20))/2))^k e^(ikθ) +(((√(20))/2))^k e^(−ikθ) ] U_n =((1−(((√(20))/2)e^(iθ) )^(n+1) )/(1−(((√(20))/2)e^(iθ) )))+((1−(((√(20))/2)e^(−iθ) )^(n+1) )/(1−(((√(20))/2)e^(−iθ) ))) U_n =((1−((√(20))/2)e^(−iθ) −(((√(20))/2)e^(iθ) )^(n+1) +(((√(20))/2))^(n+2) e^(iθn) )/(1−(((√(20))/2)e^(−iθ) )−(((√(20))/2)e^(iθ) )+((20)/4))) to be continued....](Q147189.png)
| ||
Question and Answers Forum | ||
Previous in Relation and Functions Next in Relation and Functions | ||
Question Number 146902 by mathmax by abdo last updated on 16/Jul/21 | ||
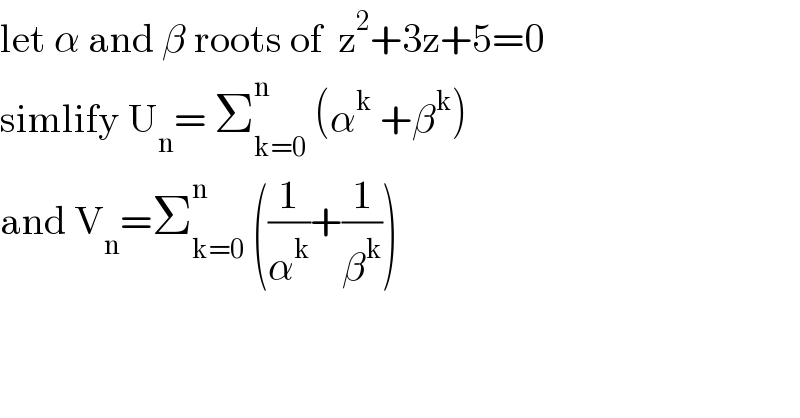 | ||
Answered by ArielVyny last updated on 18/Jul/21 | ||
![z^2 +3z+5=0→(z+(3/2))^2 −(9/4)+((20)/4)=0 (z+(3/2))^2 +((11)/4)=0 (z+(3/2)−i((√(11))/2))(z+(3/2)+i((√(11))/2))=0 then α=−(3/2)+i((√(11))/2) and β=−(3/2)−i((√(11))/2) U_n =Σ_(k=0) ^n (α^k +β^k ) ∣α∣=∣−(3/2)+i((√(11))/2)∣=(√((−(3/2))^2 +(((√(11))/2))^2 )) ∣α∣=(√((9/4)+((11)/4)))=((√(20))/2) α=((√(20))/2)(−((3/2)/((√(20))/2))+i(((√(11))/2)/((√(20))/2)))=((√(20))/2)(−(3/( (√(20))))+i((√(11))/( (√(20))))) α=((√(20))/2)e^(iθ) tel que { ((cosθ=−(3/( (√(20)))))),((sinθ=(√((11)/(20))))) :} β=((√(20))/2)e^(−iθ) U_n =Σ_(k=0) ^n [(((√(20))/2))^k e^(ikθ) +(((√(20))/2))^k e^(−ikθ) ] U_n =((1−(((√(20))/2)e^(iθ) )^(n+1) )/(1−(((√(20))/2)e^(iθ) )))+((1−(((√(20))/2)e^(−iθ) )^(n+1) )/(1−(((√(20))/2)e^(−iθ) ))) U_n =((1−((√(20))/2)e^(−iθ) −(((√(20))/2)e^(iθ) )^(n+1) +(((√(20))/2))^(n+2) e^(iθn) )/(1−(((√(20))/2)e^(−iθ) )−(((√(20))/2)e^(iθ) )+((20)/4))) to be continued....](Q147189.png) | ||
| ||