let f(a) = ∫_0 ^1 e^t ln(1+ e^(−at) )dt with a≥0 1) find f(a) 2) calculate f^′ (a) 3) find the value of ∫


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 36755 by prof Abdo imad last updated on 05/Jun/18

$l e t f (a) = \int_{0}^{1} e^{t} l n (1 + e^{- a t}) d t w i t h a ⩾ 0$ $1) f i n d f (a)$ $2) c a l c u l a t e f^{^{'}} (a)$ $3) f i n d t h e v a l u e o f \int_{0}^{1} e^{t} l n (1 + e^{- 3 t}) d t .$
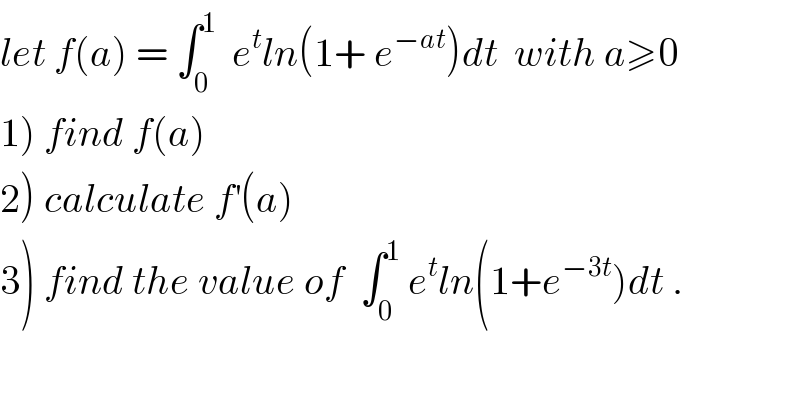
Commented by tanmay.chaudhury50@gmail.com last updated on 05/Jun/18

Commented by abdo.msup.com last updated on 05/Jun/18
$for ∣x∣<1 ln^′ (1+x) =(1/(1+x)) =Σ_(n=0) ^∞ (−1)^n x^n and ln(1+x)=Σ_(n=0) ^∞ (((−1)^n )/(n+1))x^(n+1) =Σ_(n=1) ^∞ (((−1)^(n−1) )/n)x^n ⇒ f(a)= ∫_0 ^1 e^t {Σ_(n=1) ^∞ (((−1)^(n−1) )/n) e^(−nat) }dt = Σ_(n=1) ^∞ (((−1)^(n−1) )/n) ∫_0 ^1 e^((1−na)t) dt =Σ_(n=1) ^∞ (((−1)^(n−1) )/n)(1/(1−na)){ e^(1−na) −1} =Σ_(n=1) ^∞ (((−1)^(n−1) e^(1−na) )/(n(1−na))) −Σ_(n=1) ^∞ (((−1)^(n−1) )/(n(1−na))) let w(a) =Σ_(n=1) ^∞ (((−1)^(n−1) )/(n(1−na))) ((w(a))/a) =Σ_(n=1) ^∞ (((−1)^n )/(na(na−1))) =Σ_(n=1) ^∞ (−1)^n ( (1/(na−1)) −(1/(na))) =Σ_(n=1) ^∞ (((−1))/(na−1)) −(1/a) Σ_(n=1) ^∞ (((−1)^n )/n) Σ_(n=1) ^∞ (((−1)^n )/(na−1)) +((ln(2))/a) =....be continued...$
$f o r ∣ x ∣< 1 {l n}^{^{'}} (1 + x) = \frac{1}{1 + x} = \sum_{n = 0}^{\infty} {(- 1)}^{n} x^{n}$ $a n d l n (1 + x) = \sum_{n = 0}^{\infty} \frac{{(- 1)}^{n}}{n + 1} x^{n + 1}$ $= \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1}}{n} x^{n} \Rightarrow$ $f (a) = \int_{0}^{1} e^{t} {\sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1}}{n} e^{- n a t}} d t$ $= \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1}}{n} \int_{0}^{1} e^{(1 - n a) t} d t$ $= \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1}}{n} \frac{1}{1 - n a} {e^{1 - n a} - 1}$ $= \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1} e^{1 - n a}}{n (1 - n a)}$ $- \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1}}{n (1 - n a)}$ $l e t w (a) = \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1}}{n (1 - n a)}$ $\frac{w (a)}{a} = \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n}}{n a (n a - 1)}$ $= \sum_{n = 1}^{\infty} {(- 1)}^{n} (\frac{1}{n a - 1} - \frac{1}{n a})$ $= \sum_{n = 1}^{\infty} \frac{(- 1)}{n a - 1} - \frac{1}{a} \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n}}{n}$ $\sum_{n = 1}^{\infty} \frac{{(- 1)}^{n}}{n a - 1} + \frac{l n (2)}{a} = . . . . b e c o n t i n u e d . . .$
Commented by abdo.msup.com last updated on 05/Jun/18
$2) we have f^′ (a) = ∫_0 ^1 ((−te^(−at) e^t )/(1+e^(−at) ))dt =−∫_0 ^1 (( t e^((1−a)t) )/(1+e^(−at) )) dt =−∫_0 ^1 t e^((1−a)t) {Σ_(n=1) ^∞ (((−1)^(n−1) )/n) e^(−nat) }dt =Σ_(n=1) ^∞ (((−1)^n )/n) ∫_0 ^1 t e^((1−a−na)t) dt =....$
$2) w e h a v e f^{^{'}} (a) = \int_{0}^{1} \frac{- {t e}^{- a t} e^{t}}{1 + e^{- a t}} d t$ $= - \int_{0}^{1} \frac{t e^{(1 - a) t}}{1 + e^{- a t}} d t$ $= - \int_{0}^{1} t e^{(1 - a) t} {\sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1}}{n} e^{- n a t}} d t$ $= \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n}}{n} \int_{0}^{1} t e^{(1 - a - n a) t} d t = . . . .$
Commented by abdo.msup.com last updated on 05/Jun/18
$3) ∫_0 ^1 e^t ln(1+e^(−3t) )dt = ∫_0 ^1 e^t { Σ_(n=1) ^∞ (((−1)^(n−1) )/n) e^(−3nt) )}dt =Σ_(n=1) ^∞ (((−1)^(n−1) )/n) ∫_0 ^1 e^((1−3n)t) dt =Σ_(n=1) ^∞ (((−1)^(n−1) )/n) (1/(1−3n))[ e^((1−3n)t) ]_0 ^1 =Σ_(n=1) ^∞ (((−1)^(n−1) e^(1−3n) )/(n(1−3n))) −Σ_(n=1) ^∞ (((−1)^(n−1) )/(n(1−3n))) let A_n = Σ_(n=1) ^∞ (((−1)^(n−1) )/(n(1−3n))) (A_n /3) = Σ_(n=1) ^∞ (((−1)^n )/(3n(3n−1))) =Σ_(n=1) ^∞ (−1)^n {(1/(3n−1)) −(1/(3n))} =Σ_(n=1) ^(∞ ) (((−1)^n )/(3n−1)) −(1/3) Σ_(n=1) ^∞ (((−1)^n )/n) =((ln(2))/3) +Σ_(n=1) ^∞ (((−1)^n )/(3n−1)) let f(x)=Σ_(n=1) ^∞ (−1)^n (x^(3n−1) /(3n−1)) f^′ (x) = Σ_(n=1) ^∞ (−1)^n x^(3n−2) = (1/x^2 ) Σ_(n=1) ^∞ (−x^3 )^n = (1/x^2 ) (1/(1+x^3 )) ⇒ f(x)= ∫ (dx/(x^2 (1+x^3 ))) +c ....be continued...$
$3) \int_{0}^{1} e^{t} l n (1 + e^{- 3 t}) d t$ $= \int_{0}^{1} e^{t} {\sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1}}{n} e^{- 3 n t})} d t$ $= \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1}}{n} \int_{0}^{1} e^{(1 - 3 n) t} d t$ $= \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1}}{n} \frac{1}{1 - 3 n} {[e^{(1 - 3 n) t}]}_{0}^{1}$ $= \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1} e^{1 - 3 n}}{n (1 - 3 n)}$ $- \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1}}{n (1 - 3 n)} l e t$ $A_{n} = \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1}}{n (1 - 3 n)}$ $\frac{A_{n}}{3} = \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n}}{3 n (3 n - 1)}$ $= \sum_{n = 1}^{\infty} {(- 1)}^{n} {\frac{1}{3 n - 1} - \frac{1}{3 n}}$ $= \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n}}{3 n - 1} - \frac{1}{3} \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n}}{n}$ $= \frac{l n (2)}{3} + \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n}}{3 n - 1}$ $l e t f (x) = \sum_{n = 1}^{\infty} {(- 1)}^{n} \frac{x^{3 n - 1}}{3 n - 1}$ $f^{^{'}} (x) = \sum_{n = 1}^{\infty} {(- 1)}^{n} x^{3 n - 2}$ $= \frac{1}{x^{2}} \sum_{n = 1}^{\infty} {(- x^{3})}^{n} = \frac{1}{x^{2}} \frac{1}{1 + x^{3}} \Rightarrow$ $f (x) = \int \frac{d x}{x^{2} (1 + x^{3})} + c . . . . b e c o n t i n u e d . . .$
	Answered by tanmay.chaudhury50@gmail.com last updated on 05/Jun/18
	$2)f(α)=∫_0 ^1 e^t {ln(1+e^(αt) )−lne^(αt) )}dt =∫_0 ^1 e^t {ln(1+e^(αt) )−αt}dt f′(α)=∫_0 ^1 (∂/∂α) e^t {ln(1+e^(αt) )−αt}dt =∫_0 ^1 e^t {((e^(αt) ×t)/(1+e^(αt) ))−t}dt =∫_0 ^1 e^t {((te^(αt) −t−te^(αt) )/(1+e^(αt) ))}dt =∫_0 ^1 ((−te^t )/(1+e^(αt) ))dt...contd$
	$2) f (α) = \int_{0}^{1} e^{t} {l n (1 + e^{α t}) - {l n e}^{α t})} d t$ $= \int_{0}^{1} e^{t} {l n (1 + e^{α t}) - α t} d t$ $f^{'} (α) = \int_{0}^{1} \frac{\partial}{\partial α} e^{t} {l n (1 + e^{α t}) - α t} d t$ $= \int_{0}^{1} e^{t} {\frac{e^{α t} \times t}{1 + e^{α t}} - t} d t$ $= \int_{0}^{1} e^{t} {\frac{{t e}^{α t} - t - {t e}^{α t}}{1 + e^{α t}}} d t$ $= \int_{0}^{1} \frac{- {t e}^{t}}{1 + e^{α t}} d t . . . c o n t d$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum