
Question and Answers Forum
Question Number 78269 by msup trace by abdo last updated on 15/Jan/20
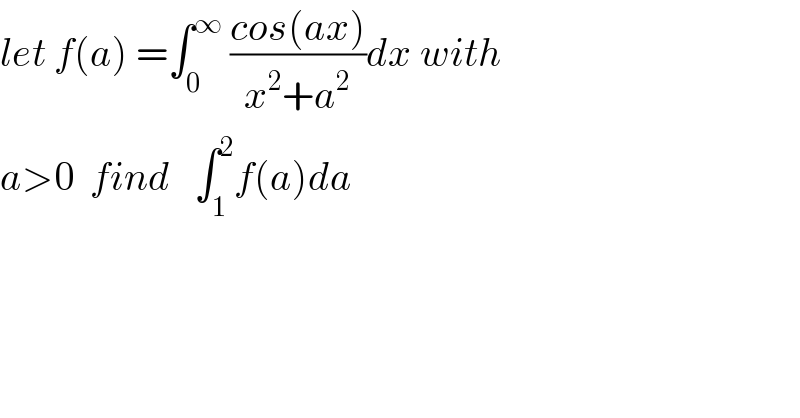
Commented by mathmax by abdo last updated on 15/Jan/20
![we have 2f(a) =∫_(−∞) ^(+∞) ((cos(ax))/(x^2 +a^2 ))dx =Re(∫_(−∞) ^(+∞) (e^(iax) /(x^2 +a^2 ))dx) let W(z)=(e^(iaz) /(z^2 +a^2 )) ⇒W(z)=(e^(iaz) /((z−ia)(z+ia))) so the poles of W are ia and −ia ⇒∫_(−∞) ^(+∞) W(z)dz =2iπ Res(W,ia) =2iπ×(e^(ia(ia)) /(2ia)) =(π/a) e^(−a^2 ) =2f(a) ⇒f(a) =(π/(2a))e^(−a^2 ) ⇒ ∫_1 ^2 f(a)da =(π/2)∫_1 ^2 (e^(−a^2 ) /a)da and a form of serie e^(−a^2 ) =Σ_(n=0) ^∞ (((−a^2 )^n )/(n!)) =Σ_(n=0) ^∞ (((−1)^n a^(2n) )/(n!)) ⇒ (e^(−a^2 ) /a) =Σ_(n=0) ^∞ (((−1)^n )/(n!)) a^(2n−1) ⇒∫_1 ^2 (e^(−a^2 ) /a)da =Σ_(n=0) ^∞ (((−1)^n )/(n!))[(1/(2n))a^(2n) ]_1 ^2 =Σ_(n=0) ^∞ (((−1)^n )/((2n)n!))( 2^(2n) −1) ⇒ ∫_1 ^2 f(a)da =(π/2)Σ_(n=0) ^∞ (((−1)^n )/((2n)n!))(4^n −1)](Q78308.png)
Answered by mind is power last updated on 15/Jan/20
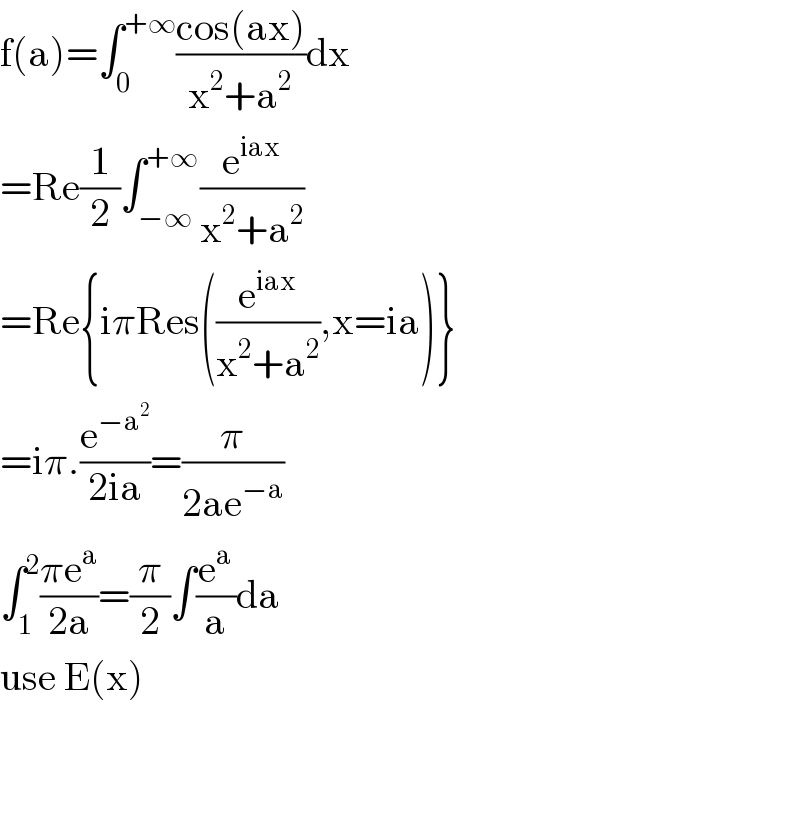
| ||
Question and Answers Forum | ||
Question Number 78269 by msup trace by abdo last updated on 15/Jan/20 | ||
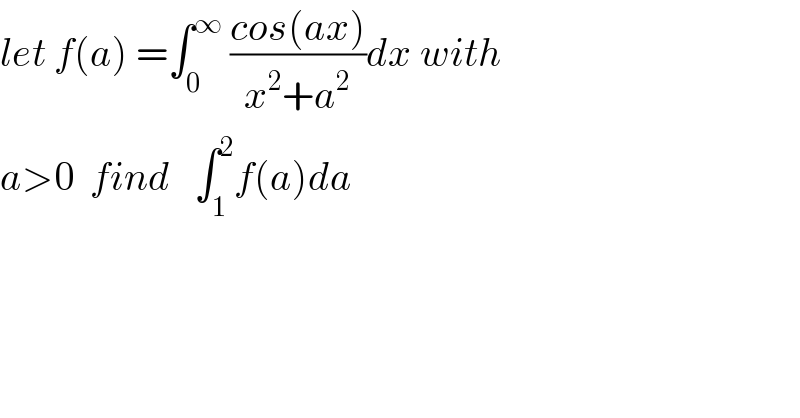 | ||
Commented by mathmax by abdo last updated on 15/Jan/20 | ||
![we have 2f(a) =∫_(−∞) ^(+∞) ((cos(ax))/(x^2 +a^2 ))dx =Re(∫_(−∞) ^(+∞) (e^(iax) /(x^2 +a^2 ))dx) let W(z)=(e^(iaz) /(z^2 +a^2 )) ⇒W(z)=(e^(iaz) /((z−ia)(z+ia))) so the poles of W are ia and −ia ⇒∫_(−∞) ^(+∞) W(z)dz =2iπ Res(W,ia) =2iπ×(e^(ia(ia)) /(2ia)) =(π/a) e^(−a^2 ) =2f(a) ⇒f(a) =(π/(2a))e^(−a^2 ) ⇒ ∫_1 ^2 f(a)da =(π/2)∫_1 ^2 (e^(−a^2 ) /a)da and a form of serie e^(−a^2 ) =Σ_(n=0) ^∞ (((−a^2 )^n )/(n!)) =Σ_(n=0) ^∞ (((−1)^n a^(2n) )/(n!)) ⇒ (e^(−a^2 ) /a) =Σ_(n=0) ^∞ (((−1)^n )/(n!)) a^(2n−1) ⇒∫_1 ^2 (e^(−a^2 ) /a)da =Σ_(n=0) ^∞ (((−1)^n )/(n!))[(1/(2n))a^(2n) ]_1 ^2 =Σ_(n=0) ^∞ (((−1)^n )/((2n)n!))( 2^(2n) −1) ⇒ ∫_1 ^2 f(a)da =(π/2)Σ_(n=0) ^∞ (((−1)^n )/((2n)n!))(4^n −1)](Q78308.png) | ||
Answered by mind is power last updated on 15/Jan/20 | ||
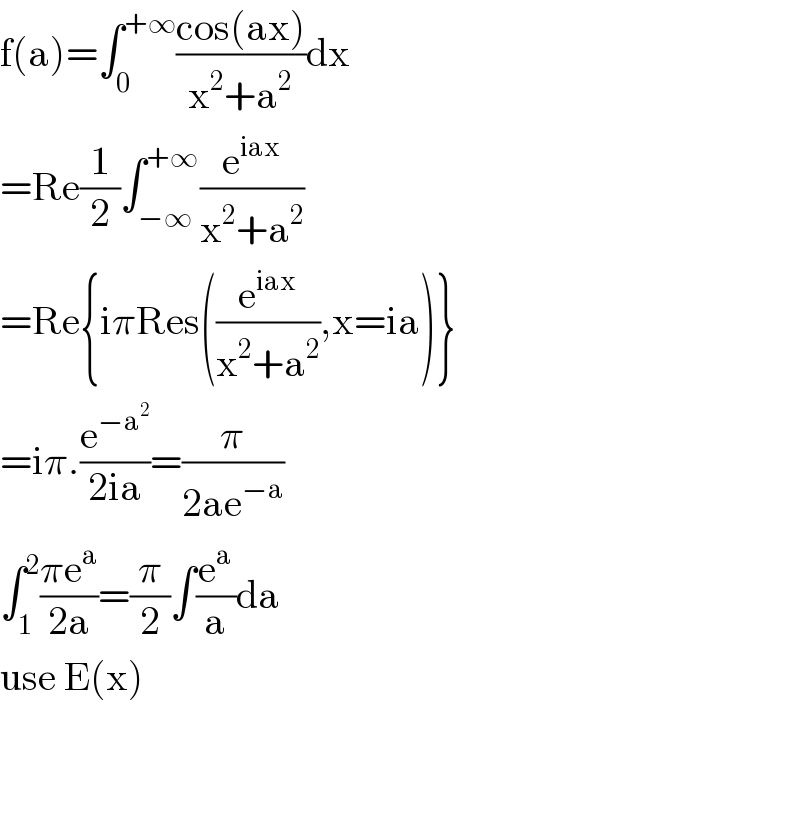 | ||
| ||