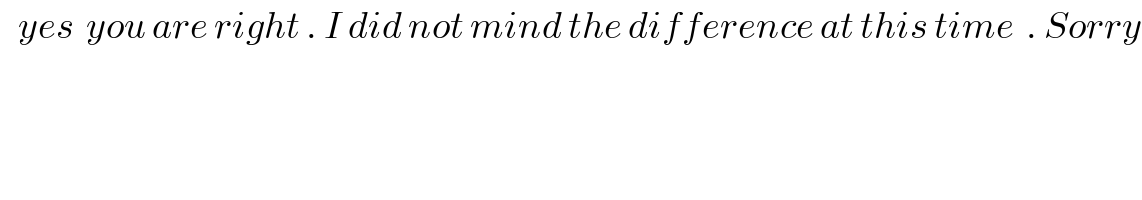Question and Answers Forum
Question Number 64970 by mathmax by abdo last updated on 23/Jul/19
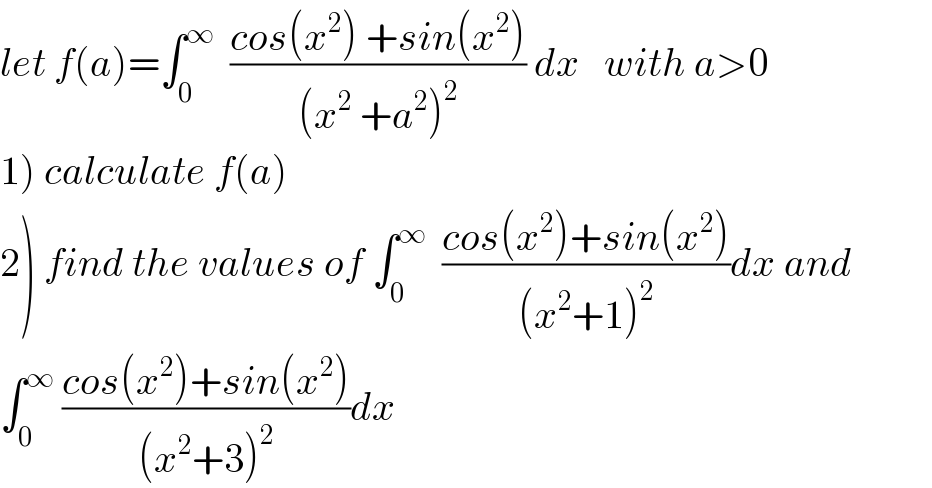
Commented by ~ À ® @ 237 ~ last updated on 23/Jul/19
![we always have cos(x^2 )+sin(x^2 )=1 so f(a)=∫_0 ^∞ (1/((x^2 +a^2 )^2 ))dx let change x =a.tant dx =a (1+tan^2 t)dt f(a) = ∫_0 ^(π/2) ((a(1+tan^2 t)dt)/((a^2 tan^2 t +a^2 )^2 )) =(1/a^3 ) ∫_0 ^(π/2) (1/((1+tan^2 t)))dt =(1/a^3 ) ∫_(0 ) ^(π/2) cos^2 t dt knowing that cos^2 t = ((1+cos2t)/2) we finally got f(a)= (1/a^3 ) [(t/2) +(1/4)sin2t]_0 ^(π/2) = (π/(4a^3 )) then f(1) = (π/4) and f((√3)) = (π/(12(√3)))](Q64979.png)
Commented by mathmax by abdo last updated on 23/Jul/19

Commented by mathmax by abdo last updated on 23/Jul/19
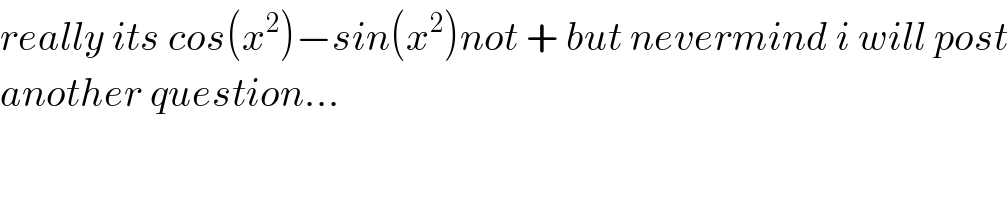
Commented by MJS last updated on 24/Jul/19
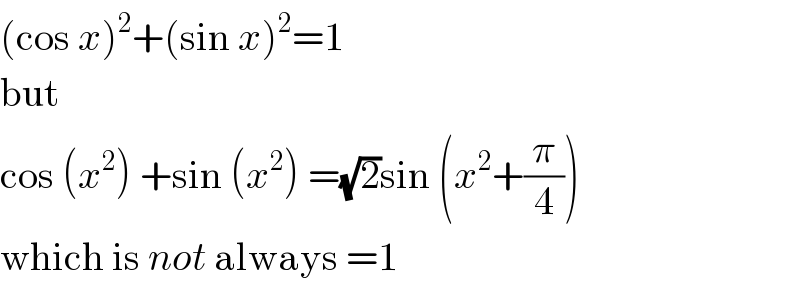
Commented by mathmax by abdo last updated on 24/Jul/19
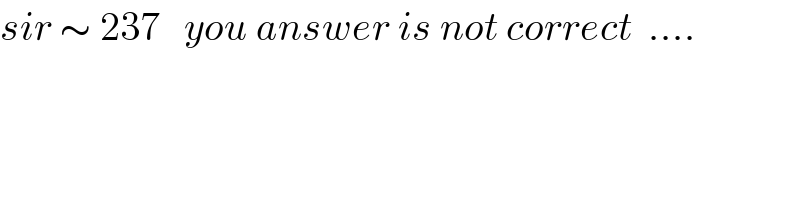
Commented by mathmax by abdo last updated on 24/Jul/19
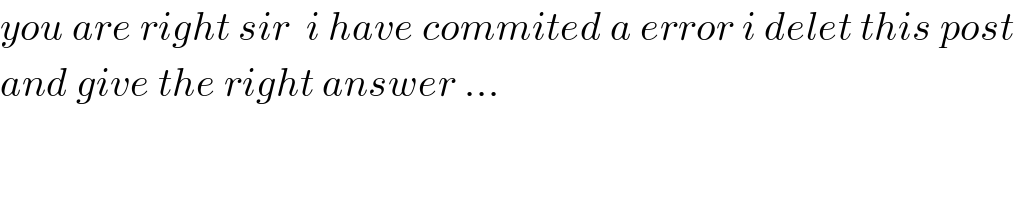
Commented by mathmax by abdo last updated on 24/Jul/19

Commented by mathmax by abdo last updated on 24/Jul/19
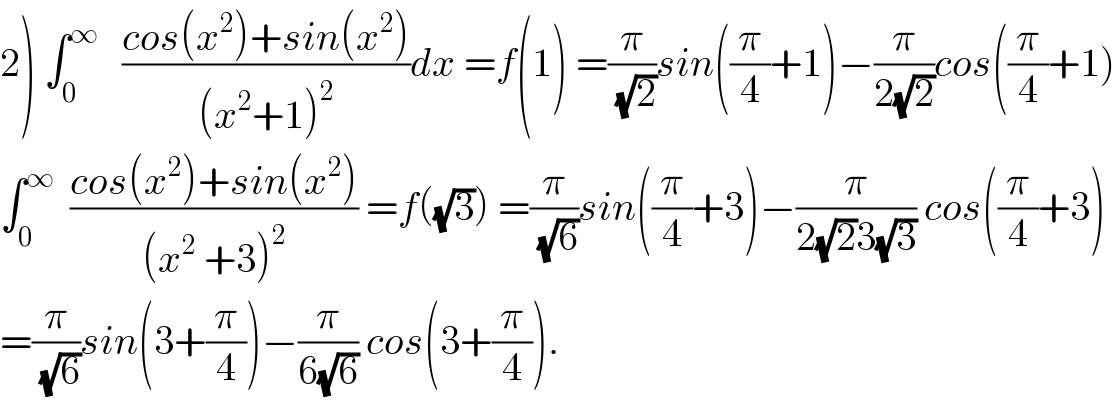
Commented by ~ À ® @ 237 ~ last updated on 25/Jul/19