
Question and Answers Forum
Question Number 61229 by maxmathsup by imad last updated on 30/May/19
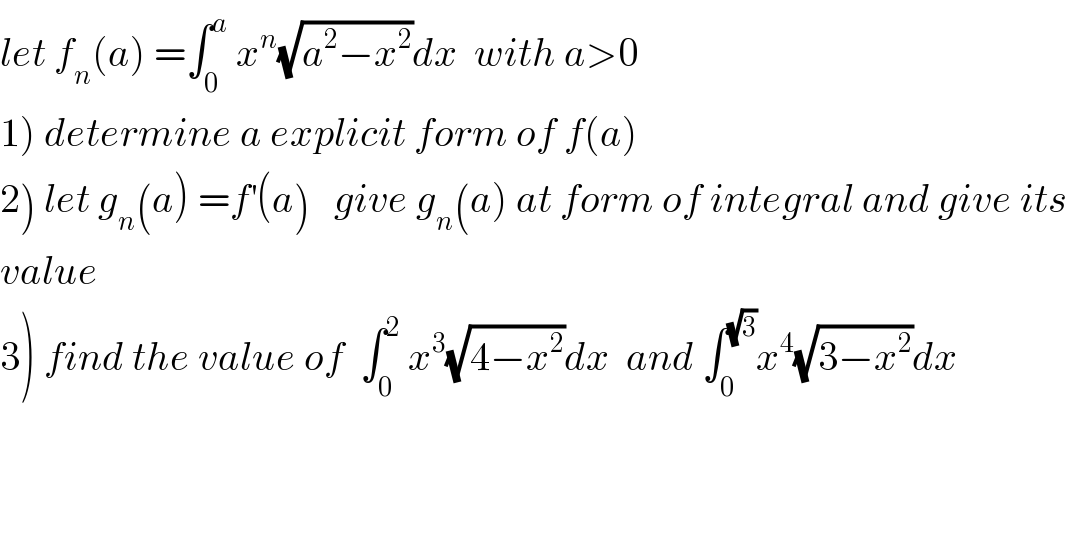
Answered by perlman last updated on 30/May/19
![1) put x=asin(t) fn(a)=a^(n+1) ∫_0 ^(π/2) sin^n (t)(√((a^2 −a^2 sin^2 (t) )) cos(t)dt= =a^(n+2) ∫_0 ^(π/2) sin^n (t)cos^2 (t)dt=a∫sin^n (t)dt−a^(n+2) ∫sin^(n+2) (t)dt let I_n =∫_0 ^(π/2) sin^n (t)dt=∫sin(t)sin^(n−1) (t)dt=[−cos(t)sin^(n−1) (t)]+(n−1)∫cos^2 (t)sin^(n−2) (t)dt (n−1)∫_0 ^(π/2) (1−sin^2 (t))sin^((n−2)) (t)dt=(n−1)I_(n−2) −(n−1)I_n =I_n I_n =((n−1)/n)I_(n−2) I_0 =(π/2) I_1 =1 I_(2n) =((2n−1)/(2n))I_(2(n−1)) I_(2n) =((2n−1)/(2n)).((2(n−1)−1)/(2(n−1)))......((2−1)/2)I_0 =(((2n−1)(2n−3)....(1))/(2n.2(n−1)....2(1)))I_0 =((2n(2n−1)(2n−2).......1)/([2^n n!]^2 ))I_0 =(((2n)!)/(2^(2n) (n!)^2 ))(π/2) I_(2n+1) =((2n)/(2n+1))I_(2n−1) =((2n)/(2n+1)).((2n−2)/(2n−1))......(2/3)I_1 =(((2^n n!)^2 .2)/((2n+1)!))=((2^(2n+1) (n!)^2 )/((2n+1)!)) fn(a)=a^(n+2) (I_n −I_(n+2) ) gn(a)=(d/da)∫_0 ^a x^n (√((a^2 −x^2 )))dx=(d/da)∫_0 ^1 a^n t^n a^2 (√((1−t^2 )))dt=∫_0 ^1 (d/da)(a^(n+2) t^n (√((1−t^2 )) dt)= (n+2)∫_0 ^1 a^(n+1) t^n (√((1−t^2 )) dt ∫_0 ^2 x^3 (√((4−x^2 )))dx n=3 a=2 =2^5 (I1−I3)=2^5 (1−(2/3))=((32)/3)](Q61248.png)
Commented by maxmathsup by imad last updated on 31/May/19

| ||
Question and Answers Forum | ||
Question Number 61229 by maxmathsup by imad last updated on 30/May/19 | ||
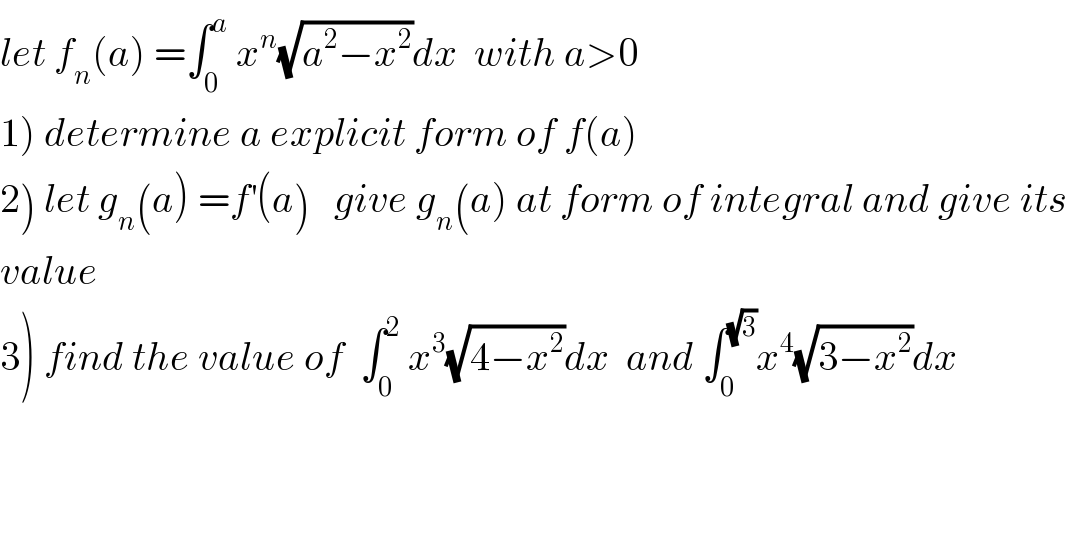 | ||
Answered by perlman last updated on 30/May/19 | ||
![1) put x=asin(t) fn(a)=a^(n+1) ∫_0 ^(π/2) sin^n (t)(√((a^2 −a^2 sin^2 (t) )) cos(t)dt= =a^(n+2) ∫_0 ^(π/2) sin^n (t)cos^2 (t)dt=a∫sin^n (t)dt−a^(n+2) ∫sin^(n+2) (t)dt let I_n =∫_0 ^(π/2) sin^n (t)dt=∫sin(t)sin^(n−1) (t)dt=[−cos(t)sin^(n−1) (t)]+(n−1)∫cos^2 (t)sin^(n−2) (t)dt (n−1)∫_0 ^(π/2) (1−sin^2 (t))sin^((n−2)) (t)dt=(n−1)I_(n−2) −(n−1)I_n =I_n I_n =((n−1)/n)I_(n−2) I_0 =(π/2) I_1 =1 I_(2n) =((2n−1)/(2n))I_(2(n−1)) I_(2n) =((2n−1)/(2n)).((2(n−1)−1)/(2(n−1)))......((2−1)/2)I_0 =(((2n−1)(2n−3)....(1))/(2n.2(n−1)....2(1)))I_0 =((2n(2n−1)(2n−2).......1)/([2^n n!]^2 ))I_0 =(((2n)!)/(2^(2n) (n!)^2 ))(π/2) I_(2n+1) =((2n)/(2n+1))I_(2n−1) =((2n)/(2n+1)).((2n−2)/(2n−1))......(2/3)I_1 =(((2^n n!)^2 .2)/((2n+1)!))=((2^(2n+1) (n!)^2 )/((2n+1)!)) fn(a)=a^(n+2) (I_n −I_(n+2) ) gn(a)=(d/da)∫_0 ^a x^n (√((a^2 −x^2 )))dx=(d/da)∫_0 ^1 a^n t^n a^2 (√((1−t^2 )))dt=∫_0 ^1 (d/da)(a^(n+2) t^n (√((1−t^2 )) dt)= (n+2)∫_0 ^1 a^(n+1) t^n (√((1−t^2 )) dt ∫_0 ^2 x^3 (√((4−x^2 )))dx n=3 a=2 =2^5 (I1−I3)=2^5 (1−(2/3))=((32)/3)](Q61248.png) | ||
| ||
Commented by maxmathsup by imad last updated on 31/May/19 | ||
 | ||