
Question and Answers Forum
Question Number 52680 by maxmathsup by imad last updated on 11/Jan/19
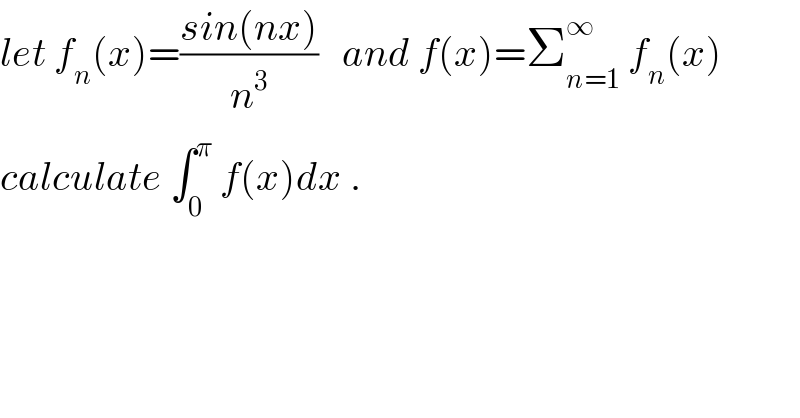
Commented by maxmathsup by imad last updated on 11/Jan/19
![its clear that the serie Σ f_n (x) converge simpl.and unif. because ∣f_n (x)∣≤(1/n^3 ) and Σ (1/n^3 ) converges we have ∫_0 ^π f(x)dx =∫_0 ^π Σ_(n=1) ^∞ ((sin(nx))/n^3 ) =Σ_(n=1) ^∞ (1/n^3 ) ∫_0 ^π sin(nx)dx =Σ_(n=1) ^∞ (1/n^3 )[−(1/n)cos(nx)]_0 ^π =Σ_(n=1) ^∞ (1/n^4 )(1−(−1)^n ) =2 Σ_(n=0) ^∞ (1/((2n+1)^4 )) but we have proved that Σ_(n=1) ^∞ (1/n^4 ) =(π^4 /(90)) ⇒ Σ_(n=0) ^∞ (1/((2n+1)^4 )) + (1/(16))Σ_(n=1) ^∞ (1/n^4 ) =(π^4 /(90)) ⇒Σ_(n=0) ^∞ (1/((2n+1)^4 )) =(π^4 /(90)) −(1/(16)) (π^4 /(90)) =(1−(1/(16)))(π^4 /(90)) =((15)/(16)) (π^4 /(90)) =((3.5)/(3.30 16)) π^4 =(π^4 /(6.16)) =(π^4 /(96)) ⇒ ∫_0 ^π f(x)dx =2 .(π^4 /(96)) ⇒ ∫_0 ^π f(x)dx =(π^4 /(48)) .](Q52704.png)
| ||
Question and Answers Forum | ||
Question Number 52680 by maxmathsup by imad last updated on 11/Jan/19 | ||
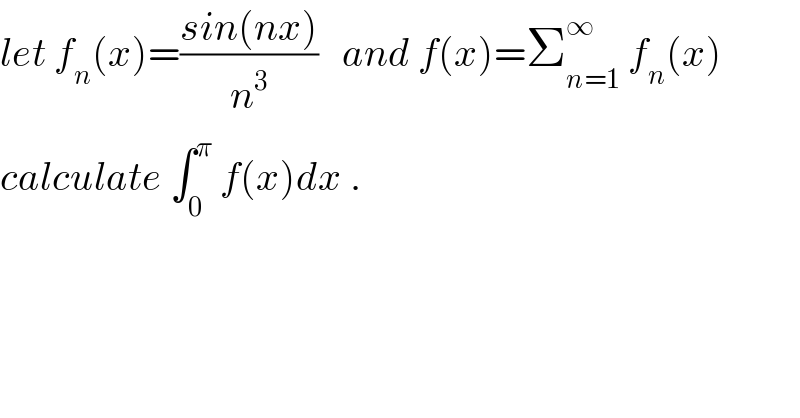 | ||
Commented by maxmathsup by imad last updated on 11/Jan/19 | ||
![its clear that the serie Σ f_n (x) converge simpl.and unif. because ∣f_n (x)∣≤(1/n^3 ) and Σ (1/n^3 ) converges we have ∫_0 ^π f(x)dx =∫_0 ^π Σ_(n=1) ^∞ ((sin(nx))/n^3 ) =Σ_(n=1) ^∞ (1/n^3 ) ∫_0 ^π sin(nx)dx =Σ_(n=1) ^∞ (1/n^3 )[−(1/n)cos(nx)]_0 ^π =Σ_(n=1) ^∞ (1/n^4 )(1−(−1)^n ) =2 Σ_(n=0) ^∞ (1/((2n+1)^4 )) but we have proved that Σ_(n=1) ^∞ (1/n^4 ) =(π^4 /(90)) ⇒ Σ_(n=0) ^∞ (1/((2n+1)^4 )) + (1/(16))Σ_(n=1) ^∞ (1/n^4 ) =(π^4 /(90)) ⇒Σ_(n=0) ^∞ (1/((2n+1)^4 )) =(π^4 /(90)) −(1/(16)) (π^4 /(90)) =(1−(1/(16)))(π^4 /(90)) =((15)/(16)) (π^4 /(90)) =((3.5)/(3.30 16)) π^4 =(π^4 /(6.16)) =(π^4 /(96)) ⇒ ∫_0 ^π f(x)dx =2 .(π^4 /(96)) ⇒ ∫_0 ^π f(x)dx =(π^4 /(48)) .](Q52704.png) | ||