let f(x) =∫_0 ^1 lnt ln(1−xt)dt with ∣x∣<1 1)determine a explicit form for f(x) 2) find also g(x) =∫_0 ^1 ((tlnt)/(1−xt))dt 3) give f^((n)) (x) at form of integral 4) calculate ∫_0 ^1 ln(t)ln(1−t)dt and ∫_0 ^1 ln(t)ln(2−t)dt 5) calculate ∫


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 64677 by mathmax by abdo last updated on 20/Jul/19

$l e t f (x) = \int_{0}^{1} l n t l n (1 - x t) d t w i t h ∣ x ∣< 1$ $1) d e t e r m i n e a e x p l i c i t f o r m f o r f (x)$ $2) f i n d a l s o g (x) = \int_{0}^{1} \frac{t l n t}{1 - x t} d t$ $3) g i v e f^{(n)} (x) a t f o r m o f i n t e g r a l$ $4) c a l c u l a t e \int_{0}^{1} l n (t) l n (1 - t) d t a n d \int_{0}^{1} l n (t) l n (2 - t) d t$ $5) c a l c u l a t e \int_{0}^{1} \frac{t l n (t)}{2 - t} d t .$
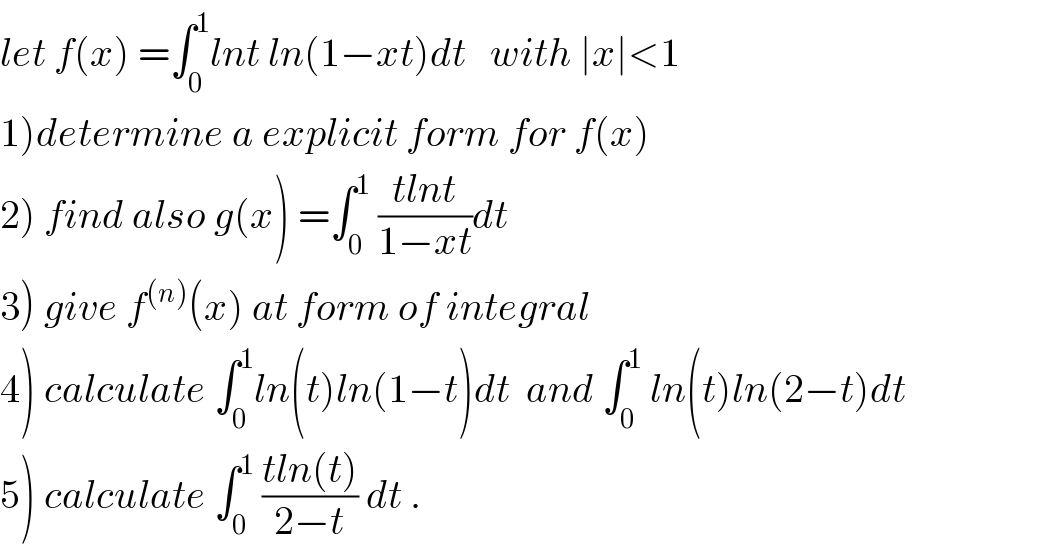
Commented by mathmax by abdo last updated on 21/Jul/19
$1) f(x) =∫_0 ^1 lntln(1−xt)dt case 1 0<x<1 changement xt =u give f(x) =∫_0 ^x ln((u/x))ln(1−u)(du/x) =(1/x) ∫_0 ^x (lnu−lnx)ln(1−u)du =(1/x) ∫_0 ^x ln(u)ln(1−u)du−((lnx)/x) ∫_0 ^x ln(1−u)du ∫_0 ^x ln(1−u)du =_(1−u =z) ∫_1 ^(1−x) ln(z)(−dz)=∫_(1−x) ^1 ln(z)dz [zlnz−z]_(1−x) ^1 =−1−((1−x)ln(1−x)−(1−x)) =−1−(1−x)ln(1−x) +1−x =−x−(1−x)ln(1−x) also we have ln^′ (1−u) =((−1)/(1−u)) =−Σ_(n=0) ^∞ u^n ⇒ ln(1−u) =−Σ_(n=0) ^∞ (u^(n+1) /(n+1)) +c (c=0) =−Σ_(n=1) ^∞ (u^n /n) ⇒ ∫_0 ^x ln(u)ln(1−u)du =−∫_0 ^x ln(u)Σ_(n=1) ^∞ (u^n /n) du =−Σ_(n=1) ^∞ (1/n) ∫_0 ^x u^n lnu du by parts f^′ =u^n and g =lnu ⇒ w_n =∫_0 ^x u^n ln(u)du =[(1/(n+1))u^(n+1) lnu]_0 ^x −∫_0 ^x (u^(n+1) /(n+1)) (du/u) =((lnx)/(n+1))x^(n+1) −(1/(n+1)) ∫_0 ^x u^n du =((lnx)/(n+1))x^(n+1) −(1/(n+1))[(u^(n+1) /(n+1))]_0 ^x =((lnx)/(n+1))x^(n+1) −(x^(n+1) /((n+1)^2 )) ⇒ ∫_0 ^x ln(u)ln(1−u)du =−Σ_(n=1) ^∞ (1/n){((lnx)/(n+1))x^(n+1) −(x^(n+1) /((n+1)^2 ))} =−lnx Σ_(n=1) ^∞ (x^(n+1) /(n(n+1))) +Σ_(n=1) ^∞ (x^(n+1) /(n(n+1)^2 )) ⇒ f(x) =−lnx Σ_(n=1) ^∞ (x^n /(n(n+1))) +Σ_(n=1) ^∞ (x^n /(n(n+1)^2 )) −((lnx)/x)(−x−(1−x)ln(1−x)) f(x) =−lnxΣ_(n=1) ^∞ (x^n /(n(n+1))) +Σ_(n=1) ^∞ (x^n /(n(n+1)^2 )) +lnx( 1+(1−x)ln(1−x)).$
$1) f (x) = \int_{0}^{1} l n t l n (1 - x t) d t c a s e 1 0 < x < 1 c h a n g e m e n t x t = u$ $g i v e f (x) = \int_{0}^{x} l n (\frac{u}{x}) l n (1 - u) \frac{d u}{x} = \frac{1}{x} \int_{0}^{x} (l n u - l n x) l n (1 - u) d u$ $= \frac{1}{x} \int_{0}^{x} l n (u) l n (1 - u) d u - \frac{l n x}{x} \int_{0}^{x} l n (1 - u) d u$ $\int_{0}^{x} l n (1 - u) d u =_{1 - u = z} \int_{1}^{1 - x} l n (z) (- d z) = \int_{1 - x}^{1} l n (z) d z$ ${[z l n z - z]}_{1 - x}^{1} = - 1 - ((1 - x) l n (1 - x) - (1 - x))$ $= - 1 - (1 - x) l n (1 - x) + 1 - x = - x - (1 - x) l n (1 - x)$ $a l s o w e h a v e {l n}^{^{'}} (1 - u) = \frac{- 1}{1 - u} = - \sum_{n = 0}^{\infty} u^{n} \Rightarrow$ $l n (1 - u) = - \sum_{n = 0}^{\infty} \frac{u^{n + 1}}{n + 1} + c (c = 0) = - \sum_{n = 1}^{\infty} \frac{u^{n}}{n} \Rightarrow$ $\int_{0}^{x} l n (u) l n (1 - u) d u = - \int_{0}^{x} l n (u) \sum_{n = 1}^{\infty} \frac{u^{n}}{n} d u$ $= - \sum_{n = 1}^{\infty} \frac{1}{n} \int_{0}^{x} u^{n} l n u d u b y p a r t s f^{^{'}} = u^{n} a n d g = l n u \Rightarrow$ $w_{n} = \int_{0}^{x} u^{n} l n (u) d u = {[\frac{1}{n + 1} u^{n + 1} l n u]}_{0}^{x} - \int_{0}^{x} \frac{u^{n + 1}}{n + 1} \frac{d u}{u}$ $= \frac{l n x}{n + 1} x^{n + 1} - \frac{1}{n + 1} \int_{0}^{x} u^{n} d u = \frac{l n x}{n + 1} x^{n + 1} - \frac{1}{n + 1} {[\frac{u^{n + 1}}{n + 1}]}_{0}^{x}$ $= \frac{l n x}{n + 1} x^{n + 1} - \frac{x^{n + 1}}{{(n + 1)}^{2}} \Rightarrow$ $\int_{0}^{x} l n (u) l n (1 - u) d u = - \sum_{n = 1}^{\infty} \frac{1}{n} {\frac{l n x}{n + 1} x^{n + 1} - \frac{x^{n + 1}}{{(n + 1)}^{2}}}$ $= - l n x \sum_{n = 1}^{\infty} \frac{x^{n + 1}}{n (n + 1)} + \sum_{n = 1}^{\infty} \frac{x^{n + 1}}{n {(n + 1)}^{2}} \Rightarrow$ $f (x) = - l n x \sum_{n = 1}^{\infty} \frac{x^{n}}{n (n + 1)} + \sum_{n = 1}^{\infty} \frac{x^{n}}{n {(n + 1)}^{2}} - \frac{l n x}{x} (- x - (1 - x) l n (1 - x))$ $f (x) = - l n x \sum_{n = 1}^{\infty} \frac{x^{n}}{n (n + 1)} + \sum_{n = 1}^{\infty} \frac{x^{n}}{n {(n + 1)}^{2}} + l n x (1 + (1 - x) l n (1 - x)) .$
Commented by mathmax by abdo last updated on 21/Jul/19
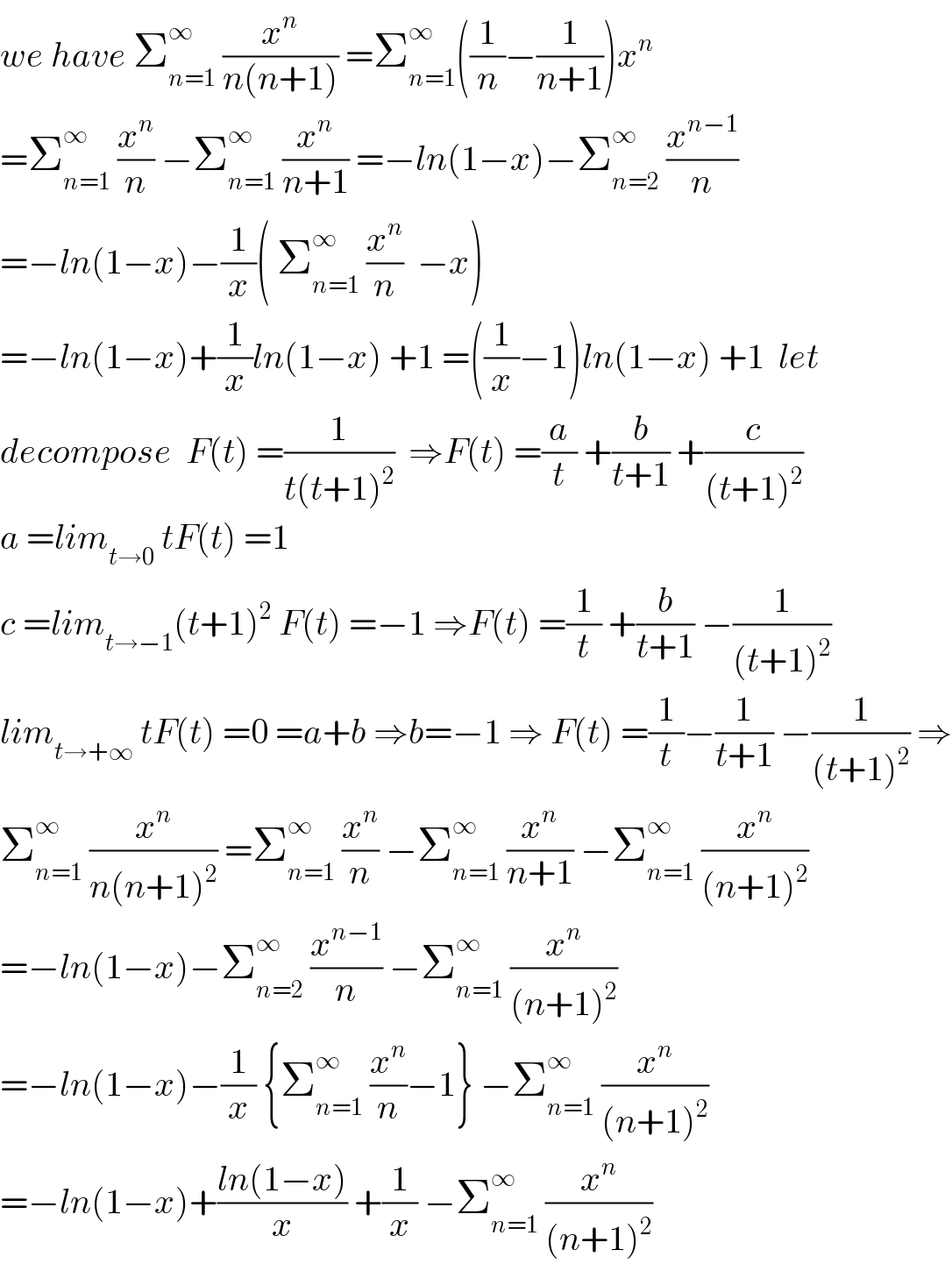
$we have Σ_(n=1) ^∞ (x^n /(n(n+1))) =Σ_(n=1) ^∞ ((1/n)−(1/(n+1)))x^n =Σ_(n=1) ^∞ (x^n /n) −Σ_(n=1) ^∞ (x^n /(n+1)) =−ln(1−x)−Σ_(n=2) ^∞ (x^(n−1) /n) =−ln(1−x)−(1/x)( Σ_(n=1) ^∞ (x^n /n) −x) =−ln(1−x)+(1/x)ln(1−x) +1 =((1/x)−1)ln(1−x) +1 let decompose F(t) =(1/(t(t+1)^2 )) ⇒F(t) =(a/t) +(b/(t+1)) +(c/((t+1)^2 )) a =lim_(t→0) tF(t) =1 c =lim_(t→−1) (t+1)^2 F(t) =−1 ⇒F(t) =(1/t) +(b/(t+1)) −(1/((t+1)^2 )) lim_(t→+∞) tF(t) =0 =a+b ⇒b=−1 ⇒ F(t) =(1/t)−(1/(t+1)) −(1/((t+1)^2 )) ⇒ Σ_(n=1) ^∞ (x^n /(n(n+1)^2 )) =Σ_(n=1) ^∞ (x^n /n) −Σ_(n=1) ^∞ (x^n /(n+1)) −Σ_(n=1) ^∞ (x^n /((n+1)^2 )) =−ln(1−x)−Σ_(n=2) ^∞ (x^(n−1) /n) −Σ_(n=1) ^∞ (x^n /((n+1)^2 )) =−ln(1−x)−(1/x) {Σ_(n=1) ^∞ (x^n /n)−1} −Σ_(n=1) ^∞ (x^n /((n+1)^2 )) =−ln(1−x)+((ln(1−x))/x) +(1/x) −Σ_(n=1) ^∞ (x^n /((n+1)^2 ))$
$w e h a v e \sum_{n = 1}^{\infty} \frac{x^{n}}{n (n + 1)} = \sum_{n = 1}^{\infty} (\frac{1}{n} - \frac{1}{n + 1}) x^{n}$ $= \sum_{n = 1}^{\infty} \frac{x^{n}}{n} - \sum_{n = 1}^{\infty} \frac{x^{n}}{n + 1} = - l n (1 - x) - \sum_{n = 2}^{\infty} \frac{x^{n - 1}}{n}$ $= - l n (1 - x) - \frac{1}{x} (\sum_{n = 1}^{\infty} \frac{x^{n}}{n} - x)$ $= - l n (1 - x) + \frac{1}{x} l n (1 - x) + 1 = (\frac{1}{x} - 1) l n (1 - x) + 1 l e t$ $d e c o m p o s e F (t) = \frac{1}{t {(t + 1)}^{2}} \Rightarrow F (t) = \frac{a}{t} + \frac{b}{t + 1} + \frac{c}{{(t + 1)}^{2}}$ $a = {l i m}_{t \to 0} t F (t) = 1$ $c = {l i m}_{t \to - 1} {(t + 1)}^{2} F (t) = - 1 \Rightarrow F (t) = \frac{1}{t} + \frac{b}{t + 1} - \frac{1}{{(t + 1)}^{2}}$ ${l i m}_{t \to + \infty} t F (t) = 0 = a + b \Rightarrow b = - 1 \Rightarrow F (t) = \frac{1}{t} - \frac{1}{t + 1} - \frac{1}{{(t + 1)}^{2}} \Rightarrow$ $\sum_{n = 1}^{\infty} \frac{x^{n}}{n {(n + 1)}^{2}} = \sum_{n = 1}^{\infty} \frac{x^{n}}{n} - \sum_{n = 1}^{\infty} \frac{x^{n}}{n + 1} - \sum_{n = 1}^{\infty} \frac{x^{n}}{{(n + 1)}^{2}}$ $= - l n (1 - x) - \sum_{n = 2}^{\infty} \frac{x^{n - 1}}{n} - \sum_{n = 1}^{\infty} \frac{x^{n}}{{(n + 1)}^{2}}$ $= - l n (1 - x) - \frac{1}{x} {\sum_{n = 1}^{\infty} \frac{x^{n}}{n} - 1} - \sum_{n = 1}^{\infty} \frac{x^{n}}{{(n + 1)}^{2}}$ $= - l n (1 - x) + \frac{l n (1 - x)}{x} + \frac{1}{x} - \sum_{n = 1}^{\infty} \frac{x^{n}}{{(n + 1)}^{2}}$
Commented by mathmax by abdo last updated on 21/Jul/19

$\sum_{n = 1}^{\infty} \frac{x^{n}}{n {(n + 1)}^{2}} = - l n (1 - x) + \frac{l n (1 - x)}{x} + 1 - \sum_{n = 1}^{\infty} \frac{x^{n}}{{(n + 1)}^{2}} \Rightarrow$ $f (x) =$
Commented by mathmax by abdo last updated on 22/Jul/19

$2) w e h a v e f^{^{'}} (x) = \int_{0}^{1} \frac{- t}{1 - x t} l n t d t = - \int_{0}^{1} \frac{t l n t}{1 - x t} d t = - g (x) \Rightarrow$ $g (x) = - f^{^{'}} (x) t h e f u n c t i o n f i s k n o w n r e s t t o c a l c u l a t e f^{^{'}} (x)$ $3) w e h a v e f^{^{'}} (x) = \int_{0}^{1} \frac{t l n t}{x t - 1} d t = \int_{0}^{1} \frac{l n t}{x - \frac{1}{t}} d t \Rightarrow$ $f^{(n)} (x) = \int_{0}^{1} {(\frac{1}{x - \frac{1}{t}})}^{(n - 1)} l n t d t = \int_{0}^{1} \frac{{(- 1)}^{n - 1} (n - 1)!}{{(x - \frac{1}{t})}^{n}} l n t d t$ $f^{(n)} (x) = {(- 1)}^{n - 1} (n - 1)! \int_{0}^{1} \frac{t^{n} l n t}{{(x t - 1)}^{n}} d t$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum