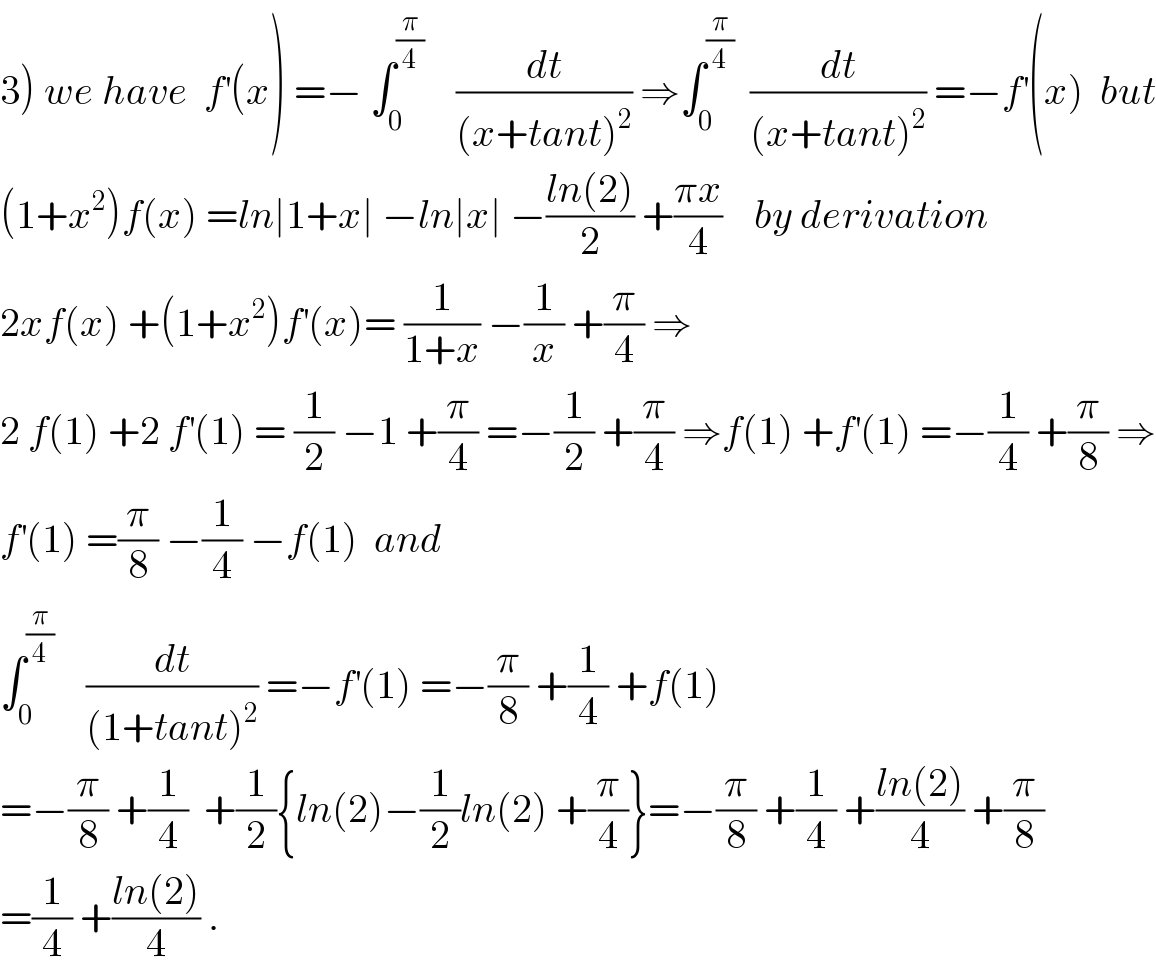let f(x) = ∫_0 ^(π/4) (dt/(x +tan(t))) 1) find anoher expression off (x) 2) calculate ∫_0 ^(π/4) (dt/(2+tan(t))) and A(θ) = ∫_0 ^(π/4) (dt/(sinθ+tant)) 3) calculate ∫


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 41847 by maxmathsup by imad last updated on 13/Aug/18

$l e t f (x) = \int_{0}^{\frac{π}{4}} \frac{d t}{x + t a n (t)}$ $1) f i n d a n o h e r e x p r e s s i o n o f f (x)$ $2) c a l c u l a t e \int_{0}^{\frac{π}{4}} \frac{d t}{2 + t a n (t)} a n d A (θ) = \int_{0}^{\frac{π}{4}} \frac{d t}{s i n θ + t a n t}$ $3) c a l c u l a t e \int_{0}^{\frac{π}{4}} \frac{d t}{{(1 + t a n t)}^{2}}$
	Answered by maxmathsup by imad last updated on 14/Aug/18
	$1) we have f(x) = ∫_0 ^(π/4) (dt/(x+tant)) changement tant =u give f(x) = ∫_0 ^1 (du/((1+u^2 )(x+u))) let decompose F(u) = (1/((x+u)(1+u^2 ))) F(u) =(a/(x+u)) +((bu +c)/(u^2 +1)) a =lim_(u→−x) (x+u)F(u) = (1/(1+x^2 )) lim_(u→+∞) uF(u) =0 =a +b ⇒b=−(1/(1+x^2 )) ⇒F(u)=(1/((1+x^2 )(u+x))) +((−(1/(1+x^2 ))u +c)/(u^2 +1)) F(0) =(1/x) = (1/(x(1+x^2 ))) +c ⇒1 =(1/(1+x^2 )) +xc ⇒xc =1−(1/(1+x^2 )) ⇒ xc =(x^2 /(1+x^2 )) ⇒ c =(x/(1+x^2 )) ( we suppose x≠0) ⇒ F(u) = (1/((1+x^2 )(u+x))) −(1/(1+x^2 )) ((u−x)/(u^2 +1)) ⇒ f(x) = (1/(1+x^2 )) { ∫_0 ^1 (du/(u+x)) −(1/2)∫_0 ^1 ((2u)/(u^2 +1))du +x ∫_0 ^1 (du/(1+u^2 ))} =(1/(1+x^2 )){ [ln∣u+x∣_0 ^1 −(1/2)[ln∣u^2 +1∣]_0 ^1 +x [arctanu ]_0 ^1 } f(x)=(1/(1+x^2 )){ ln∣1+x∣−ln∣x∣ −(1/2)ln(2) +((πx)/4)}$
	$1) w e h a v e f (x) = \int_{0}^{\frac{π}{4}} \frac{d t}{x + t a n t} c h a n g e m e n t t a n t = u g i v e$ $f (x) = \int_{0}^{1} \frac{d u}{(1 + u^{2}) (x + u)} l e t d e c o m p o s e F (u) = \frac{1}{(x + u) (1 + u^{2})}$ $F (u) = \frac{a}{x + u} + \frac{b u + c}{u^{2} + 1}$ $a = {l i m}_{u \to - x} (x + u) F (u) = \frac{1}{1 + x^{2}}$ ${l i m}_{u \to + \infty} u F (u) = 0 = a + b \Rightarrow b = - \frac{1}{1 + x^{2}} \Rightarrow F (u) = \frac{1}{(1 + x^{2}) (u + x)} + \frac{- \frac{1}{1 + x^{2}} u + c}{u^{2} + 1}$ $F (0) = \frac{1}{x} = \frac{1}{x (1 + x^{2})} + c \Rightarrow 1 = \frac{1}{1 + x^{2}} + x c \Rightarrow x c = 1 - \frac{1}{1 + x^{2}} \Rightarrow$ $x c = \frac{x^{2}}{1 + x^{2}} \Rightarrow c = \frac{x}{1 + x^{2}} (w e s u p p o s e x \neq 0) \Rightarrow$ $F (u) = \frac{1}{(1 + x^{2}) (u + x)} - \frac{1}{1 + x^{2}} \frac{u - x}{u^{2} + 1} \Rightarrow$ $f (x) = \frac{1}{1 + x^{2}} {\int_{0}^{1} \frac{d u}{u + x} - \frac{1}{2} \int_{0}^{1} \frac{2 u}{u^{2} + 1} d u + x \int_{0}^{1} \frac{d u}{1 + u^{2}}}$ $= \frac{1}{1 + x^{2}} {[l n ∣ u + x ∣_{0}^{1} - \frac{1}{2} {[l n ∣ u^{2} + 1 ∣]}_{0}^{1} + x {[a r c t a n u]}_{0}^{1}}$ $f (x) = \frac{1}{1 + x^{2}} {l n ∣ 1 + x ∣ - l n ∣ x ∣ - \frac{1}{2} l n (2) + \frac{π x}{4}}$
	Commented by maxmathsup by imad last updated on 14/Aug/18
	$2) ∫_0 ^(π/4) (dt/(2 +tan(t))) =f(2) = (1/5){ ln(3)−ln(2)−(1/2)ln(2) +(π/2)} =(1/5){ ln(3)−(3/2)ln(2) +(π/2)} also we have ∫_0 ^(π/4) (dt/(sinθ +tant)) =f(sinθ) =(1/(1+sin^2 θ)){ ln(1+sin^2 θ)−ln∣sinθ∣−(1/2)ln(2)+((πsinπ)/4)}$
	$2) \int_{0}^{\frac{π}{4}} \frac{d t}{2 + t a n (t)} = f (2) = \frac{1}{5} {l n (3) - l n (2) - \frac{1}{2} l n (2) + \frac{π}{2}}$ $= \frac{1}{5} {l n (3) - \frac{3}{2} l n (2) + \frac{π}{2}} a l s o w e h a v e$ $\int_{0}^{\frac{π}{4}} \frac{d t}{s i n θ + t a n t} = f (s i n θ) = \frac{1}{1 + {s i n}^{2} θ} {l n (1 + {s i n}^{2} θ) - l n ∣ s i n θ ∣ - \frac{1}{2} l n (2) + \frac{π s i n π}{4}}$
	Commented by maxmathsup by imad last updated on 14/Aug/18
	$3) we have f^′ (x) =− ∫_0 ^(π/4) (dt/((x+tant)^2 )) ⇒∫_0 ^(π/4) (dt/((x+tant)^2 )) =−f^′ (x) but (1+x^2 )f(x) =ln∣1+x∣ −ln∣x∣ −((ln(2))/2) +((πx)/4) by derivation 2xf(x) +(1+x^2 )f^′ (x)= (1/(1+x)) −(1/x) +(π/4) ⇒ 2 f(1) +2 f^′ (1) = (1/2) −1 +(π/4) =−(1/2) +(π/4) ⇒f(1) +f^′ (1) =−(1/4) +(π/8) ⇒ f^′ (1) =(π/8) −(1/4) −f(1) and ∫_0 ^(π/4) (dt/((1+tant)^2 )) =−f^′ (1) =−(π/8) +(1/4) +f(1) =−(π/8) +(1/4) +(1/2){ln(2)−(1/2)ln(2) +(π/4)}=−(π/8) +(1/4) +((ln(2))/4) +(π/8) =(1/4) +((ln(2))/4) .$
	$3) w e h a v e f^{^{'}} (x) = - \int_{0}^{\frac{π}{4}} \frac{d t}{{(x + t a n t)}^{2}} \Rightarrow \int_{0}^{\frac{π}{4}} \frac{d t}{{(x + t a n t)}^{2}} = - f^{^{'}} (x) b u t$ $(1 + x^{2}) f (x) = l n ∣ 1 + x ∣ - l n ∣ x ∣ - \frac{l n (2)}{2} + \frac{π x}{4} b y d e r i v a t i o n$ $2 x f (x) + (1 + x^{2}) f^{^{'}} (x) = \frac{1}{1 + x} - \frac{1}{x} + \frac{π}{4} \Rightarrow$ $2 f (1) + 2 f^{^{'}} (1) = \frac{1}{2} - 1 + \frac{π}{4} = - \frac{1}{2} + \frac{π}{4} \Rightarrow f (1) + f^{^{'}} (1) = - \frac{1}{4} + \frac{π}{8} \Rightarrow$ $f^{^{'}} (1) = \frac{π}{8} - \frac{1}{4} - f (1) a n d$ $\int_{0}^{\frac{π}{4}} \frac{d t}{{(1 + t a n t)}^{2}} = - f^{^{'}} (1) = - \frac{π}{8} + \frac{1}{4} + f (1)$ $= - \frac{π}{8} + \frac{1}{4} + \frac{1}{2} {l n (2) - \frac{1}{2} l n (2) + \frac{π}{4}} = - \frac{π}{8} + \frac{1}{4} + \frac{l n (2)}{4} + \frac{π}{8}$ $= \frac{1}{4} + \frac{l n (2)}{4} .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum