
Question and Answers Forum
Question Number 40152 by maxmathsup by imad last updated on 16/Jul/18
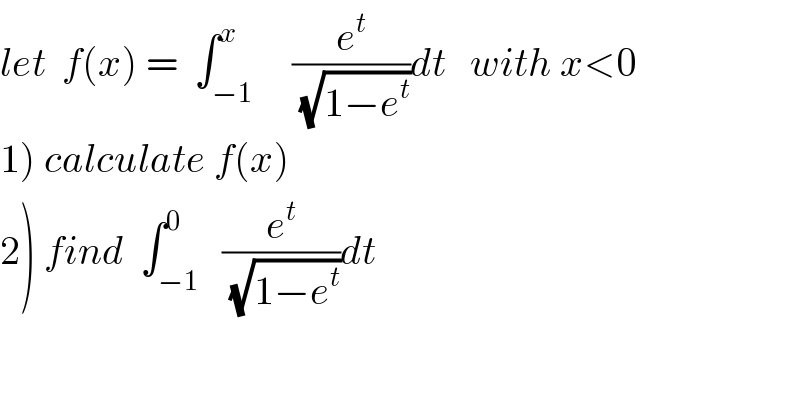
Commented by maxmathsup by imad last updated on 16/Jul/18
![changement e^t =u give t=ln(u) ⇒ f(x)= ∫_e^(−1) ^e^x (u/(√(1−u))) (du/u) = ∫_e^(−1) ^e^x (du/(√(1−u))) =[−2(√(1−u))]_e^(−1) ^e^x f(x)=−2{(√(1−e^x )) −(√(1−e^(−1) ))} 2) ∫_(−1) ^0 (e^t /(√(1−e^t ))) dt =lim_(x→0) f(x)= 2(√(1−e^(−1) ))](Q40196.png)
Answered by tanmay.chaudhury50@gmail.com last updated on 16/Jul/18

| ||
Question and Answers Forum | ||
Question Number 40152 by maxmathsup by imad last updated on 16/Jul/18 | ||
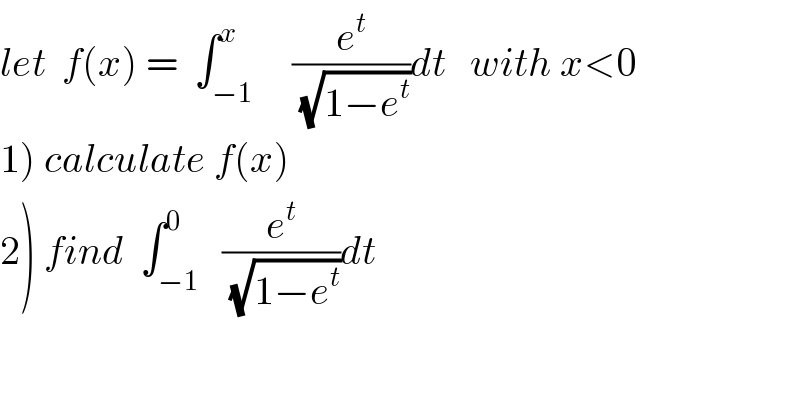 | ||
Commented by maxmathsup by imad last updated on 16/Jul/18 | ||
![changement e^t =u give t=ln(u) ⇒ f(x)= ∫_e^(−1) ^e^x (u/(√(1−u))) (du/u) = ∫_e^(−1) ^e^x (du/(√(1−u))) =[−2(√(1−u))]_e^(−1) ^e^x f(x)=−2{(√(1−e^x )) −(√(1−e^(−1) ))} 2) ∫_(−1) ^0 (e^t /(√(1−e^t ))) dt =lim_(x→0) f(x)= 2(√(1−e^(−1) ))](Q40196.png) | ||
Answered by tanmay.chaudhury50@gmail.com last updated on 16/Jul/18 | ||
 | ||
| ||