let f(x)= e^(−2x) arctan(x^2 ) 1)calculate f^((n)) (x) 2) find f^((n)) (0) 3) developp f at integr serie


Question and Answers Forum

All Questions Topic List
Others Questions
Previous in All Question Next in All Question
Previous in Others Next in Others
Question Number 37838 by math khazana by abdo last updated on 18/Jun/18

$l e t f (x) = e^{- 2 x} a r c t a n (x^{2})$ $1) c a l c u l a t e f^{(n)} (x)$ $2) f i n d f^{(n)} (0)$ $3) d e v e l o p p f a t i n t e g r s e r i e$
Commented by math khazana by abdo last updated on 20/Jun/18
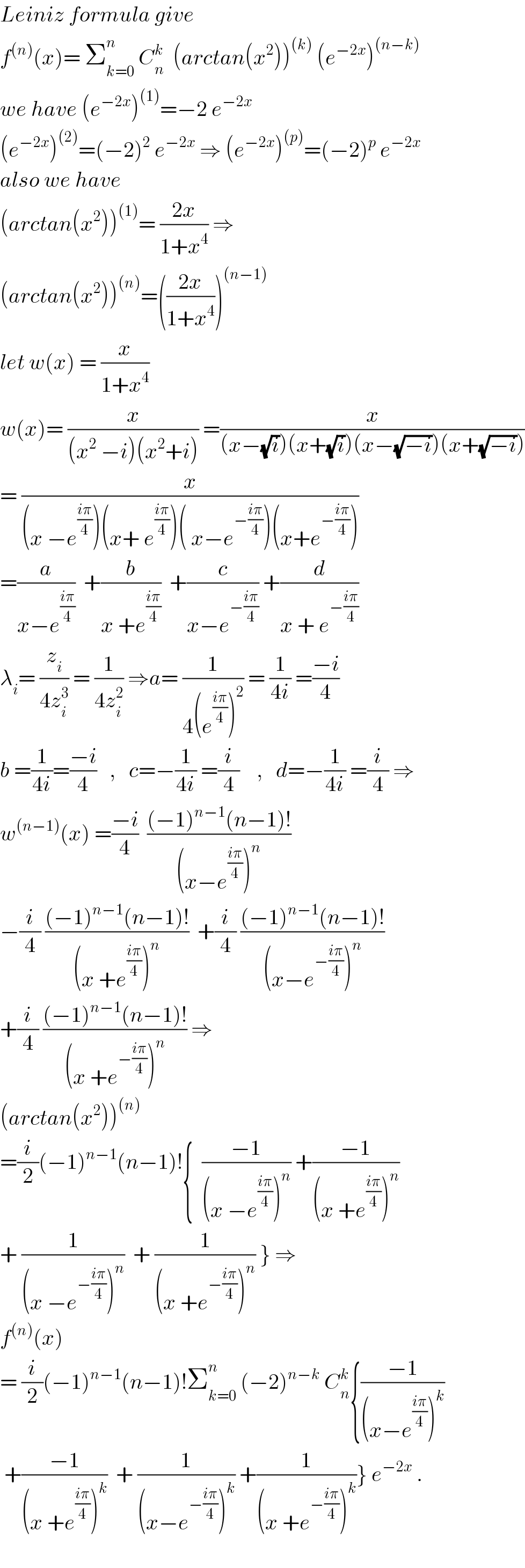
$Leiniz formula give f^((n)) (x)= Σ_(k=0) ^n C_n ^k (arctan(x^2 ))^((k)) (e^(−2x) )^((n−k)) we have (e^(−2x) )^((1)) =−2 e^(−2x) (e^(−2x) )^((2)) =(−2)^2 e^(−2x) ⇒ (e^(−2x) )^((p)) =(−2)^p e^(−2x) also we have (arctan(x^2 ))^((1)) = ((2x)/(1+x^4 )) ⇒ (arctan(x^2 ))^((n)) =(((2x)/(1+x^4 )))^((n−1)) let w(x) = (x/(1+x^4 )) w(x)= (x/((x^2 −i)(x^2 +i))) =(x/((x−(√i))(x+(√i))(x−(√(−i)))(x+(√(−i))))) = (x/((x −e^((iπ)/4) )(x+ e^((iπ)/4) )( x−e^(−((iπ)/4)) )(x+e^(−((iπ)/4)) ))) =(a/(x−e^((iπ)/4) )) +(b/(x +e^((iπ)/4) )) +(c/(x−e^(−((iπ)/4)) )) +(d/(x + e^(−((iπ)/4)) )) λ_i = (z_i /(4z_i ^3 )) = (1/(4z_i ^2 )) ⇒a= (1/(4(e^((iπ)/4) )^2 )) = (1/(4i)) =((−i)/4) b =(1/(4i))=((−i)/4) , c=−(1/(4i)) =(i/4) , d=−(1/(4i)) =(i/4) ⇒ w^((n−1)) (x) =((−i)/4) (((−1)^(n−1) (n−1)!)/((x−e^((iπ)/4) )^n )) −(i/4) (((−1)^(n−1) (n−1)!)/((x +e^((iπ)/4) )^n )) +(i/4) (((−1)^(n−1) (n−1)!)/((x−e^(−((iπ)/4)) )^n )) +(i/4) (((−1)^(n−1) (n−1)!)/((x +e^(−((iπ)/4)) )^n )) ⇒ (arctan(x^2 ))^((n)) =(i/2)(−1)^(n−1) (n−1)!{ ((−1)/((x −e^((iπ)/4) )^n )) +((−1)/((x +e^((iπ)/4) )^n )) + (1/((x −e^(−((iπ)/4)) )^n )) + (1/((x +e^(−((iπ)/4)) )^n )) } ⇒ f^((n)) (x) = (i/2)(−1)^(n−1) (n−1)!Σ_(k=0) ^n (−2)^(n−k) C_n ^k {((−1)/((x−e^((iπ)/4) )^k )) +((−1)/((x +e^((iπ)/4) )^k )) + (1/((x−e^(−((iπ)/4)) )^k )) +(1/((x +e^(−((iπ)/4)) )^k ))} e^(−2x) .$
$L e i n i z f o r m u l a g i v e$ $f^{(n)} (x) = \sum_{k = 0}^{n} C_{n}^{k} {(a r c t a n (x^{2}))}^{(k)} {(e^{- 2 x})}^{(n - k)}$ $w e h a v e {(e^{- 2 x})}^{(1)} = - 2 e^{- 2 x}$ ${(e^{- 2 x})}^{(2)} = {(- 2)}^{2} e^{- 2 x} \Rightarrow {(e^{- 2 x})}^{(p)} = {(- 2)}^{p} e^{- 2 x}$ $a l s o w e h a v e$ ${(a r c t a n (x^{2}))}^{(1)} = \frac{2 x}{1 + x^{4}} \Rightarrow$ ${(a r c t a n (x^{2}))}^{(n)} = {(\frac{2 x}{1 + x^{4}})}^{(n - 1)}$ $l e t w (x) = \frac{x}{1 + x^{4}}$ $w (x) = \frac{x}{(x^{2} - i) (x^{2} + i)} = \frac{x}{(x - \sqrt{i}) (x + \sqrt{i}) (x - \sqrt{- i}) (x + \sqrt{- i})}$ $= \frac{x}{(x - e^{\frac{i π}{4}}) (x + e^{\frac{i π}{4}}) (x - e^{- \frac{i π}{4}}) (x + e^{- \frac{i π}{4}})}$ $= \frac{a}{x - e^{\frac{i π}{4}}} + \frac{b}{x + e^{\frac{i π}{4}}} + \frac{c}{x - e^{- \frac{i π}{4}}} + \frac{d}{x + e^{- \frac{i π}{4}}}$ $λ_{i} = \frac{z_{i}}{4 z_{i}^{3}} = \frac{1}{4 z_{i}^{2}} \Rightarrow a = \frac{1}{4 {(e^{\frac{i π}{4}})}^{2}} = \frac{1}{4 i} = \frac{- i}{4}$ $b = \frac{1}{4 i} = \frac{- i}{4}, c = - \frac{1}{4 i} = \frac{i}{4}, d = - \frac{1}{4 i} = \frac{i}{4} \Rightarrow$ $w^{(n - 1)} (x) = \frac{- i}{4} \frac{{(- 1)}^{n - 1} (n - 1)!}{{(x - e^{\frac{i π}{4}})}^{n}}$ $- \frac{i}{4} \frac{{(- 1)}^{n - 1} (n - 1)!}{{(x + e^{\frac{i π}{4}})}^{n}} + \frac{i}{4} \frac{{(- 1)}^{n - 1} (n - 1)!}{{(x - e^{- \frac{i π}{4}})}^{n}}$ $+ \frac{i}{4} \frac{{(- 1)}^{n - 1} (n - 1)!}{{(x + e^{- \frac{i π}{4}})}^{n}} \Rightarrow$ ${(a r c t a n (x^{2}))}^{(n)}$ $= \frac{i}{2} {(- 1)}^{n - 1} (n - 1)! {\frac{- 1}{{(x - e^{\frac{i π}{4}})}^{n}} + \frac{- 1}{{(x + e^{\frac{i π}{4}})}^{n}}$ $+ \frac{1}{{(x - e^{- \frac{i π}{4}})}^{n}} + \frac{1}{{(x + e^{- \frac{i π}{4}})}^{n}}} \Rightarrow$ $f^{(n)} (x)$ $= \frac{i}{2} {(- 1)}^{n - 1} (n - 1)! \sum_{k = 0}^{n} {(- 2)}^{n - k} C_{n}^{k} {\frac{- 1}{{(x - e^{\frac{i π}{4}})}^{k}}$ $+ \frac{- 1}{{(x + e^{\frac{i π}{4}})}^{k}} + \frac{1}{{(x - e^{- \frac{i π}{4}})}^{k}} + \frac{1}{{(x + e^{- \frac{i π}{4}})}^{k}}} e^{- 2 x} .$
Commented by math khazana by abdo last updated on 20/Jun/18
$error of calculus at the final line f^((n)) (x) =(i/2) Σ_(k=0) ^n (−2)^(n−k) (−1)^(k−1) (k−1)! C_n ^k { ((−1)/((x−e^((iπ)/4) )^k )) +((−1)/((x +e^((iπ)/4) )^k )) + (1/((x−e^(−((iπ)/4)) )^k )) +(1/((x+e^(−((iπ)/4)) )^k ))}e^(−2x)$
$e r r o r o f c a l c u l u s a t t h e f i n a l l i n e$ $f^{(n)} (x) = \frac{i}{2} \sum_{k = 0}^{n} {(- 2)}^{n - k} {(- 1)}^{k - 1} (k - 1)! C_{n}^{k} {$ $\frac{- 1}{{(x - e^{\frac{i π}{4}})}^{k}} + \frac{- 1}{{(x + e^{\frac{i π}{4}})}^{k}} + \frac{1}{{(x - e^{- \frac{i π}{4}})}^{k}} + \frac{1}{{(x + e^{- \frac{i π}{4}})}^{k}}} e^{- 2 x}$
Commented by math khazana by abdo last updated on 20/Jun/18
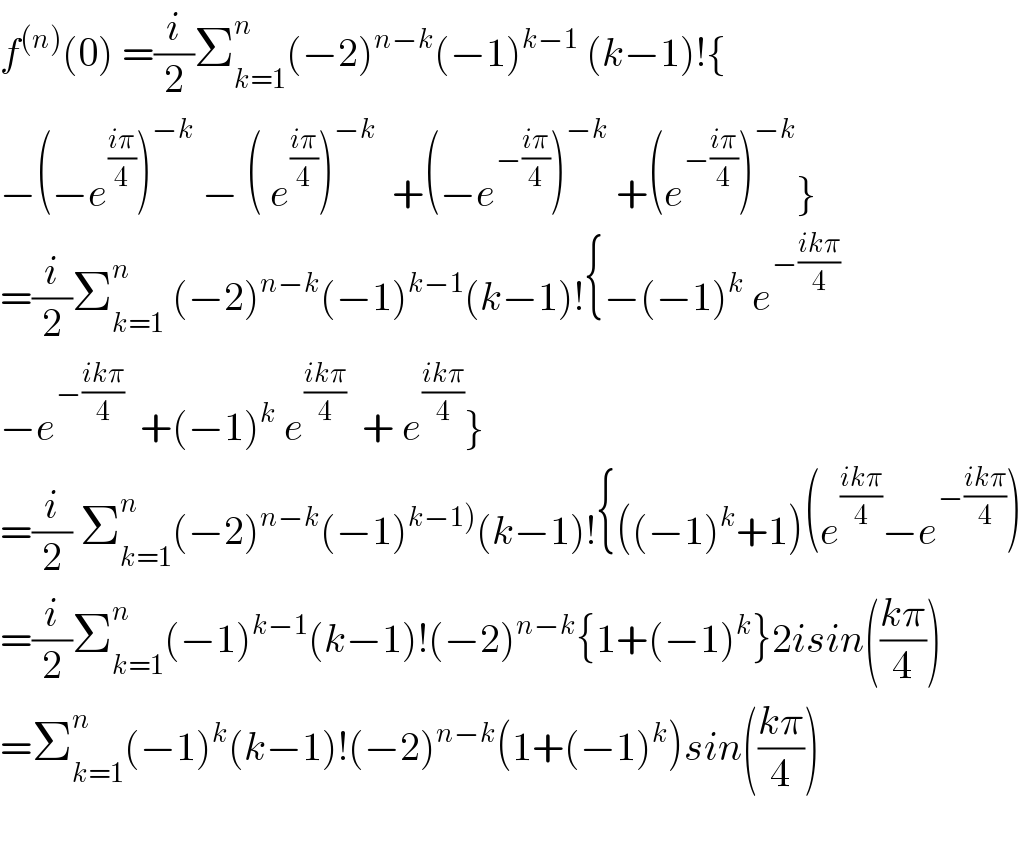
$f^((n)) (0) =(i/2)Σ_(k=1) ^n (−2)^(n−k) (−1)^(k−1) (k−1)!{ −(−e^((iπ)/4) )^(−k) − ( e^((iπ)/4) )^(−k) +(−e^(−((iπ)/4)) )^(−k) +(e^(−((iπ)/4)) )^(−k) } =(i/2)Σ_(k=1) ^n (−2)^(n−k) (−1)^(k−1) (k−1)!{−(−1)^k e^(−((ikπ)/4)) −e^(−((ikπ)/4)) +(−1)^k e^((ikπ)/4) + e^((ikπ)/4) } =(i/2) Σ_(k=1) ^n (−2)^(n−k) (−1)^(k−1)) (k−1)!{((−1)^k +1)(e^((ikπ)/4) −e^(−((ikπ)/4)) ) =(i/2)Σ_(k=1) ^n (−1)^(k−1) (k−1)!(−2)^(n−k) {1+(−1)^k }2isin(((kπ)/4)) =Σ_(k=1) ^n (−1)^k (k−1)!(−2)^(n−k) (1+(−1)^k )sin(((kπ)/4))$
$f^{(n)} (0) = \frac{i}{2} \sum_{k = 1}^{n} {(- 2)}^{n - k} {(- 1)}^{k - 1} (k - 1)! {$ $- {(- e^{\frac{i π}{4}})}^{- k} - {(e^{\frac{i π}{4}})}^{- k} + {(- e^{- \frac{i π}{4}})}^{- k} + {(e^{- \frac{i π}{4}})}^{- k}}$ $= \frac{i}{2} \sum_{k = 1}^{n} {(- 2)}^{n - k} {(- 1)}^{k - 1} (k - 1)! {- {(- 1)}^{k} e^{- \frac{i k π}{4}}$ $- e^{- \frac{i k π}{4}} + {(- 1)}^{k} e^{\frac{i k π}{4}} + e^{\frac{i k π}{4}}}$ $= \frac{i}{2} \sum_{k = 1}^{n} {(- 2)}^{n - k} {(- 1)}^{k - 1)} (k - 1)! {({(- 1)}^{k} + 1) (e^{\frac{i k π}{4}} - e^{- \frac{i k π}{4}})$ $= \frac{i}{2} \sum_{k = 1}^{n} {(- 1)}^{k - 1} (k - 1)! {(- 2)}^{n - k} {1 + {(- 1)}^{k}} 2 i s i n (\frac{k π}{4})$ $= \sum_{k = 1}^{n} {(- 1)}^{k} (k - 1)! {(- 2)}^{n - k} (1 + {(- 1)}^{k}) s i n (\frac{k π}{4})$
Commented by math khazana by abdo last updated on 20/Jun/18
$3) f(x)=Σ_(n=0) ^∞ ((f^((n)) (0))/(n!)) x^n = 2 Σ_(n=1) ^∞ (1/(n!)){Σ_(p=1) ^([(n/2)]) (2p−1)!(−2)^(n−2p) sin(((pπ)/2))}x^n$
$3) f (x) = \sum_{n = 0}^{\infty} \frac{f^{(n)} (0)}{n!} x^{n}$ $= 2 \sum_{n = 1}^{\infty} \frac{1}{n!} {\sum_{p = 1}^{[\frac{n}{2}]} (2 p - 1)! {(- 2)}^{n - 2 p} s i n (\frac{p π}{2})} x^{n}$
Commented by math khazana by abdo last updated on 20/Jun/18

$f^{(n)} (0) = \sum_{p = 1}^{[\frac{n}{2}]} (2 p - 1)! {(- 2)}^{n - 2 p} s i n (\frac{p π}{2}) .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum