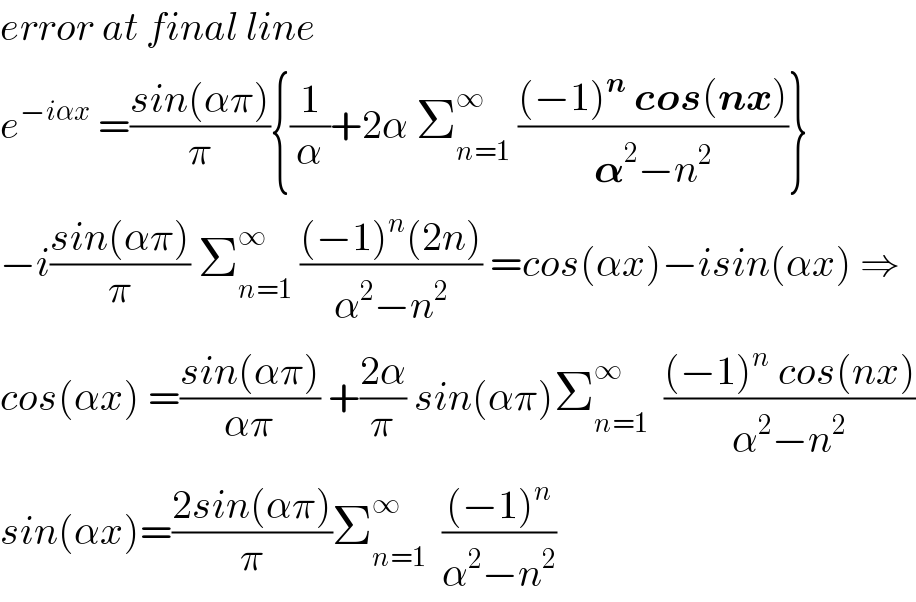Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 68035 by mathmax by abdo last updated on 03/Sep/19
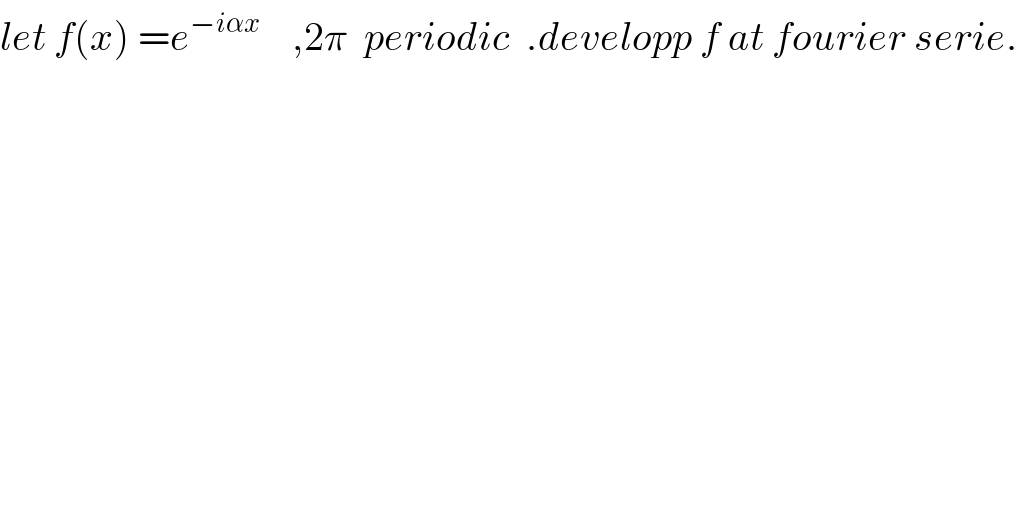
Commented by mathmax by abdo last updated on 08/Sep/19
![f(x) =Σ_(n=−∞) ^(+∞) a_n e^(inwx) with w =((2π)/T) =1 ⇒ f(x)=Σ_(n=−∞) ^(+∞) a_n e^(inx) and a_n =(1/T)∫_(−(T/2)) ^(T/2) f(x)e^(−inx) dx =(1/(2π)) ∫_(−π) ^π e^(−iαx) e^(−inx) dx =(1/(2π)) ∫_(−π) ^π e^(−i(α+n)x) dx ⇒ 2π a_n =∫_(−π) ^π e^(−i(α+n)x) dx =[(1/(−i(α+n)))e^(−i(α+n)x) ]_(−π) ^π =((−1)/(i(α+n))){ e^(−i(α+n)π) −e^(−i(α+n)(−π)) } =(i/(α+n)){ (−1)^n e^(−iπα) −(−1)^n e^(iπα) } =((−i(−1)^n )/(α+n)){ e^(iπα) −e^(−iπα) } =((−i(−1)^n )/(n+α)) (2isin(πα)) =((2(−1)^n sin(πα))/(n+α)) ⇒ e^(−iαx) =Σ_(n=−∞) ^(+∞) ((2(−1)^n sin(πα))/(n+α)) e^(inx) =2sin(πα) Σ_(n=−∞) ^(+∞) (((−1)^n )/(n+α)) e^(inx) .](Q68263.png)
Commented by mathmax by abdo last updated on 08/Sep/19
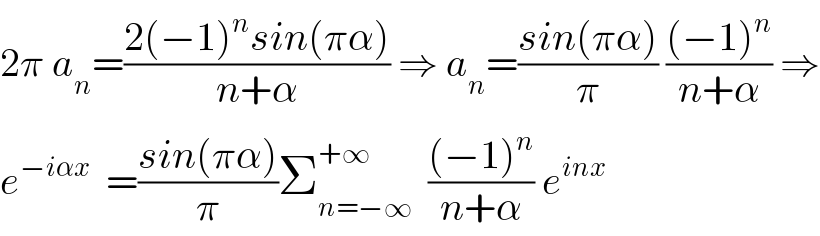
Commented by mathmax by abdo last updated on 08/Sep/19

Commented by mathmax by abdo last updated on 08/Sep/19