let f(x)=ln∣((x−1)/(x+1))∣ 1)determine D_f 2) calculatef^((n)) (x) and f^((n)) (0) 3) developp f at integr serie 4) calculate ∫


Question and Answers Forum

All Questions Topic List
Relation and Functions Questions
Previous in All Question Next in All Question
Previous in Relation and Functions Next in Relation and Functions
Question Number 62882 by mathmax by abdo last updated on 26/Jun/19

$l e t f (x) = l n ∣ \frac{x - 1}{x + 1} ∣$ $1) d e t e r m i n e D_{f}$ $2) {c a l c u l a t e f}^{(n)} (x) a n d f^{(n)} (0)$ $3) d e v e l o p p f a t i n t e g r s e r i e$ $4) c a l c u l a t e \int_{- \frac{1}{2}}^{\frac{1}{2}} f (x) d x .$
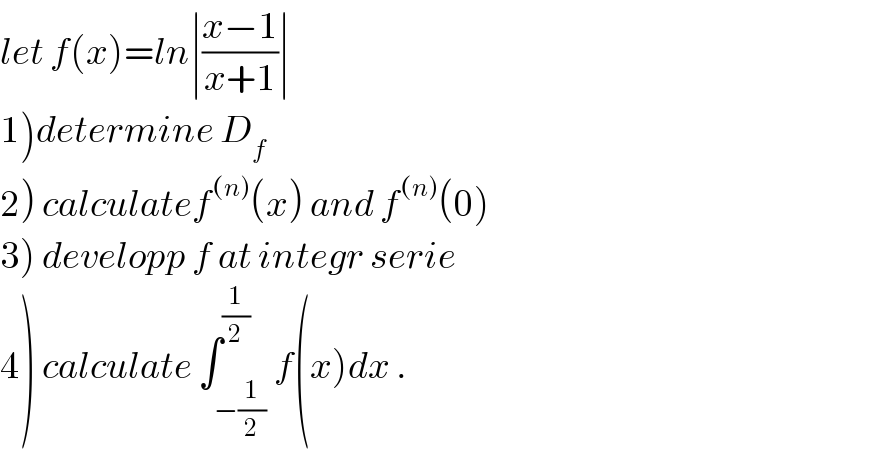
Commented by mathmax by abdo last updated on 27/Jun/19

$4) \int_{- \frac{1}{2}}^{\frac{1}{2}} l n ∣ \frac{x - 1}{x + 1} ∣ d x = \int_{- \frac{1}{2}}^{\frac{1}{2}} l n ∣ 1 - x ∣ d x - \int_{- \frac{1}{2}}^{\frac{1}{2}} l n ∣ 1 + x ∣ d x$ $= \int_{- \frac{1}{2}}^{\frac{1}{2}} l n (1 - x) d x - \int_{- \frac{1}{2}}^{\frac{1}{2}} l n (1 + x) d x = H - K$ $H =_{1 - x = t} \int_{\frac{3}{2}}^{\frac{1}{2}} l n (t) (- d t) = \int_{\frac{1}{2}}^{\frac{3}{2}} l n (t) d t = {[t l n (t) - t]}_{\frac{1}{2}}^{\frac{3}{2}}$ $= \frac{3}{2} l n (\frac{3}{2}) - \frac{3}{2} - \frac{1}{2} l n (\frac{1}{2}) + \frac{1}{2}$ $K = \int_{- \frac{1}{2}}^{\frac{1}{2}} l n (1 + x) d x =_{1 + x = t} \int_{\frac{1}{2}}^{\frac{3}{2}} l n (t) d t = {[t l n (t) - t]}_{\frac{1}{2}}^{\frac{3}{2}}$ $= \frac{3}{2} l n (\frac{3}{2}) - \frac{3}{2} - \frac{1}{2} l n (\frac{1}{2}) + \frac{1}{2} \Rightarrow$ $A = \frac{3}{2} l n (\frac{3}{2}) - \frac{3}{2} - \frac{1}{2} l n (\frac{1}{2}) + \frac{1}{2} - \frac{3}{2} l n (\frac{3}{2}) + \frac{3}{2} + \frac{1}{2} l n (\frac{1}{2}) - \frac{1}{2} \Rightarrow$ $A = 0$ $a n o t h e r [w a y l e t p r o v e t h a t f i s o d d w e h a v e$ $f (- x) = l n ∣ \frac{- x - 1}{- x + 1} ∣ = l n ∣ \frac{x + 1}{x - 1} ∣ = - l n ∣ \frac{x - 1}{x + 1} ∣= - f (x) \Rightarrow \int_{- \frac{1}{2}}^{\frac{1}{2}} f (x) d x = 0 .$
Commented by mathmax by abdo last updated on 27/Jun/19
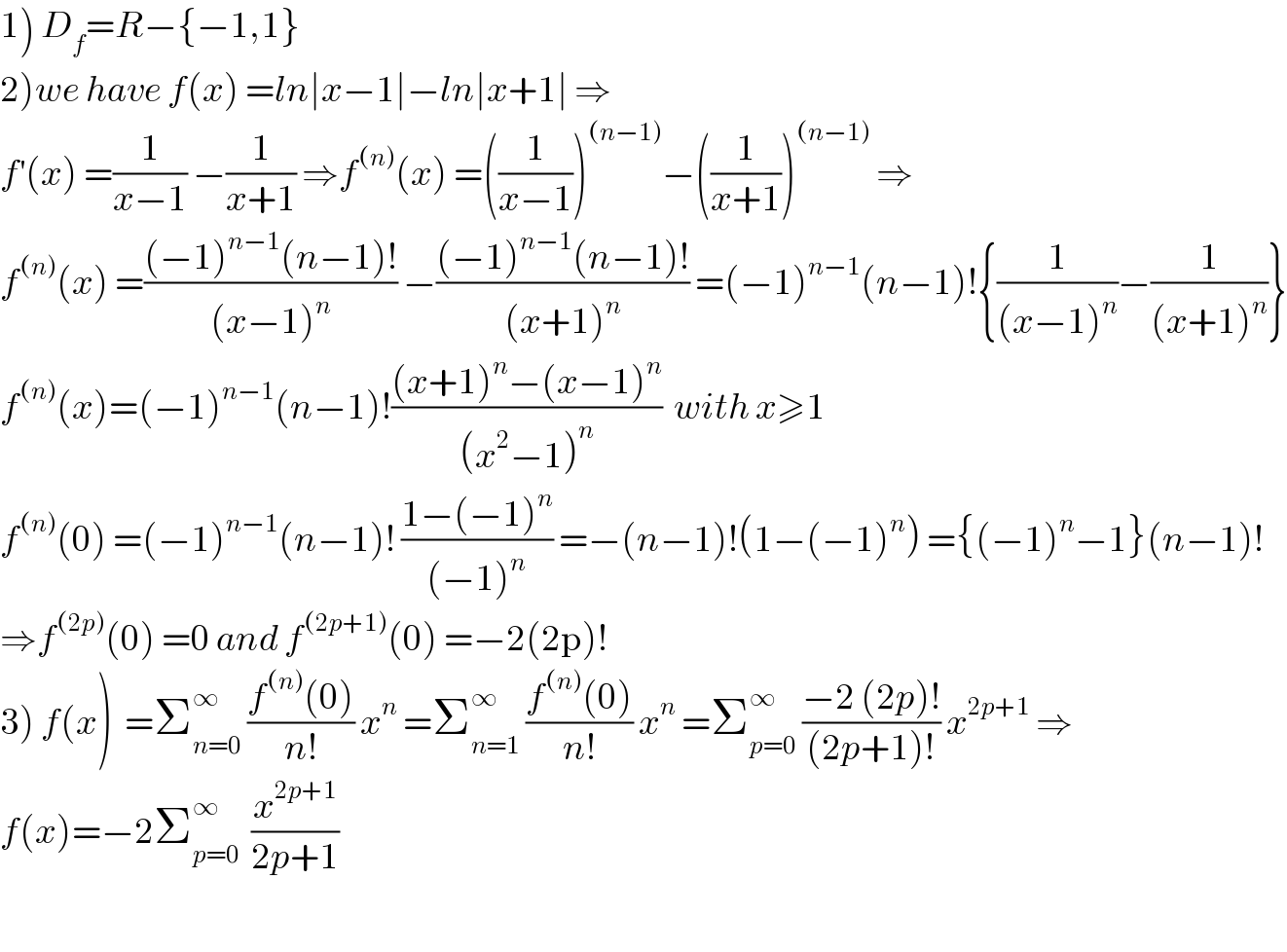
$1) D_f =R−{−1,1} 2)we have f(x) =ln∣x−1∣−ln∣x+1∣ ⇒ f^′ (x) =(1/(x−1)) −(1/(x+1)) ⇒f^((n)) (x) =((1/(x−1)))^((n−1)) −((1/(x+1)))^((n−1)) ⇒ f^((n)) (x) =(((−1)^(n−1) (n−1)!)/((x−1)^n )) −(((−1)^(n−1) (n−1)!)/((x+1)^n )) =(−1)^(n−1) (n−1)!{(1/((x−1)^n ))−(1/((x+1)^n ))} f^((n)) (x)=(−1)^(n−1) (n−1)!(((x+1)^n −(x−1)^n )/((x^2 −1)^n )) with x≥1 f^((n)) (0) =(−1)^(n−1) (n−1)! ((1−(−1)^n )/((−1)^n )) =−(n−1)!(1−(−1)^n ) ={(−1)^n −1}(n−1)! ⇒f^((2p)) (0) =0 and f^((2p+1)) (0) =−2(2p)! 3) f(x) =Σ_(n=0) ^∞ ((f^((n)) (0))/(n!)) x^n =Σ_(n=1) ^∞ ((f^((n)) (0))/(n!)) x^n =Σ_(p=0) ^∞ ((−2 (2p)!)/((2p+1)!)) x^(2p+1) ⇒ f(x)=−2Σ_(p=0) ^∞ (x^(2p+1) /(2p+1))$
$1) D_{f} = R - {- 1, 1}$ $2) w e h a v e f (x) = l n ∣ x - 1 ∣ - l n ∣ x + 1 ∣ \Rightarrow$ $f^{^{'}} (x) = \frac{1}{x - 1} - \frac{1}{x + 1} \Rightarrow f^{(n)} (x) = {(\frac{1}{x - 1})}^{(n - 1)} - {(\frac{1}{x + 1})}^{(n - 1)} \Rightarrow$ $f^{(n)} (x) = \frac{{(- 1)}^{n - 1} (n - 1)!}{{(x - 1)}^{n}} - \frac{{(- 1)}^{n - 1} (n - 1)!}{{(x + 1)}^{n}} = {(- 1)}^{n - 1} (n - 1)! {\frac{1}{{(x - 1)}^{n}} - \frac{1}{{(x + 1)}^{n}}}$ $f^{(n)} (x) = {(- 1)}^{n - 1} (n - 1)! \frac{{(x + 1)}^{n} - {(x - 1)}^{n}}{{(x^{2} - 1)}^{n}} w i t h x ⩾ 1$ $f^{(n)} (0) = {(- 1)}^{n - 1} (n - 1)! \frac{1 - {(- 1)}^{n}}{{(- 1)}^{n}} = - (n - 1)! (1 - {(- 1)}^{n}) = {{(- 1)}^{n} - 1} (n - 1)!$ $\Rightarrow f^{(2 p)} (0) = 0 a n d f^{(2 p + 1)} (0) = - 2 (2 p)!$ $3) f (x) = \sum_{n = 0}^{\infty} \frac{f^{(n)} (0)}{n!} x^{n} = \sum_{n = 1}^{\infty} \frac{f^{(n)} (0)}{n!} x^{n} = \sum_{p = 0}^{\infty} \frac{- 2 (2 p)!}{(2 p + 1)!} x^{2 p + 1} \Rightarrow$ $f (x) = - 2 \sum_{p = 0}^{\infty} \frac{x^{2 p + 1}}{2 p + 1}$
Commented by mathmax by abdo last updated on 27/Jun/19

$s o r r y i h a v e f l a g e d t h e p o s t b y e r r o r . . .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum