let f(x)=∫_x ^(x^2 +3) e^(−xt) ln(1+e^(−xt) )dt with x>0 1) calculate f(x) 2)find lim


Question and Answers Forum

All Questions Topic List
Relation and Functions Questions
Previous in All Question Next in All Question
Previous in Relation and Functions Next in Relation and Functions
Question Number 74017 by mathmax by abdo last updated on 17/Nov/19

$l e t f (x) = \int_{x}^{x^{2} + 3} e^{- x t} l n (1 + e^{- x t}) d t w i t h x > 0$ $1) c a l c u l a t e f (x)$ $2) f i n d {l i m}_{x \to + \infty} f (x) .$
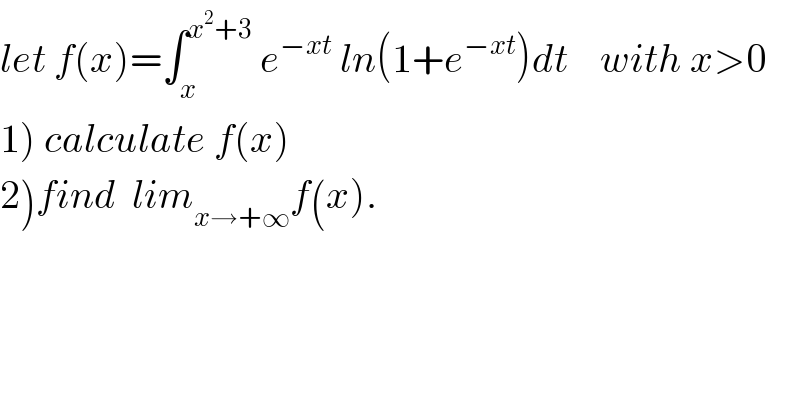
Commented by mathmax by abdo last updated on 17/Nov/19

$1) c a l c u l a t e f^{^{'}} (x)$
Commented by mind is power last updated on 17/Nov/19
$u=xt⇒du=xdt f(x)=(1/x)∫_x^2 ^(x^3 +3x) e^(−u) ln(1+e^(−u) )du ∫e^(−u) ln(1+e^(−u) )du =−e^(−u) ln(1+e^(−u) )−∫(e^(−2u) /(1+e^(−u) ))du =−e^(−u) ln(1+e^(−u) )−∫(((e^(−u) +1)(e^(−u) −1))/((1+e^(−u) )))−∫(e^u /(e^u +1))du =−e^(−u) ln(1+e^(−u) )+∫(−e^(−u) +1)du−ln(e^u +1) =−e^(−u) ln(1+e^(−u) )+e^(−u) +u−ln(e^u +1)+c f(x)=(1/x){[−e^(−(x^3 +3x)) ln(1+e^(−x^3 −3x) )+e^(−(x^3 +3x)) +(x^3 +3x)−ln(e^(x^3 +3x) +1)] +e^(−x^2 ) ln(1+e^(−x^2 ) )−e^(−x^2 ) −x^2 +ln(e^x^2 +1))] lim f(x)=0$
$u = xt \Rightarrow du = xdt$ $f (x) = \frac{1}{x} \int_{x^{2}}^{x^{3} + 3 x} e^{- u} \ln (1 + e^{- u}) du$ $\int e^{- u} \ln (1 + e^{- u}) du$ $= - e^{- u} \ln (1 + e^{- u}) - \int \frac{e^{- 2 u}}{1 + e^{- u}} du$ $= - e^{- u} \ln (1 + e^{- u}) - \int \frac{(e^{- u} + 1) (e^{- u} - 1)}{(1 + e^{- u})} - \int \frac{e^{u}}{e^{u} + 1} du$ $= - e^{- u} \ln (1 + e^{- u}) + \int (- e^{- u} + 1) du - \ln (e^{u} + 1)$ $= - e^{- u} \ln (1 + e^{- u}) + e^{- u} + u - \ln (e^{u} + 1) + c$ $f (x) = \frac{1}{x} {[- e^{- (x^{3} + 3 x)} \ln (1 + e^{- x^{3} - 3 x}) + e^{- (x^{3} + 3 x)} + (x^{3} + 3 x) - \ln (e^{x^{3} + 3 x} + 1)]$ $+ e^{- x^{2}} \ln (1 + e^{- x^{2}}) - e^{- x^{2}} - x^{2} + \ln (e^{x^{2}} + 1))]$ $\lim f (x) = 0$
Commented by mathmax by abdo last updated on 21/Nov/19
$1) we have f(x)=∫_x ^(x^2 +3) e^(−xt) ln(1+e^(−xt) )dt (x>0) changement xt=u give f(x)=(1/x)∫_x^2 ^(x^3 +3x) e^(−u) ln(1+e^(−u) )du ⇒ xf(x)=∫_x^2 ^(x^3 +3x) e^(−u) ln(1+e^(−u) )dy =_(bypsrts) [−e^(−u) ln(1+e^(−u) )]_x^2 ^(x^3 +3x) −∫_x^2 ^(x^3 +3x) (−e^(−u) )×((−e^(−u) )/(1+e^(−u) )) du =e^(−x^2 ) ln(1+e^(−x^2 ) ) −e^(−(x^3 +3x)) ln(1+e^(−(x^3 +3x)) ) +∫_x^2 ^(x^3 +3x) (e^(−2u) /(1+e^(−u) ))du we have ∫_x^2 ^(x^3 +3x) (e^(−2u) /(1+e^(−u) ))du =∫_x^2 ^(x^3 +3x) (1/(e^(2u) +e^u ))du =_(e^u =z) ∫_e^x^2 ^e^(x^3 +3x) (1/(z^2 +z))(dz/z) = ∫_e^x^2 ^e^(x^3 +3x) (dz/(z^2 (z+1))) decomposition of F(z)=(1/(z^2 (z+1))) F(z)=(a/z) +(b/z^2 ) +(c/(z+1)) b=1 , c=1 ⇒F(z)=(a/z) +(1/z^2 ) +(1/(z+1)) lim_(z→+∞) zF(z)=0=a+c ⇒a=−c=−1 ⇒F(z)=−(1/z)+(1/z^2 ) +(1/(z+1)) ∫_e^x^2 ^e^(x^3 +3x) (dz/(z^2 (z+1))) =[ln∣((z+1)/z)∣]_e^x^2 ^e^(x^3 +3x) +[−(1/z)]_e^x^2 ^e^(x^3 +3x) =ln(((1+e^(x^3 +3x) )/e^(x^3 +3x) ))−ln(((1+e^x^2 )/e^x^2 ))+(e^(−x^2 ) −e^(−(x^3 +3x)) ) ⇒ f(x)=(1/x){e^(−x^2 ) ln(1+e^(−x^2 ) )−e^(−(x^3 +3x)) ln(1+e^(−(x^3 +3x)) ) ln(((1+e^(x^3 +3x) )/e^(x^3 +3x) ))−ln(((1+e^x^2 )/e^x^2 )) +e^(−x^2 ) −e^(−(x^3 +3x)) } 2) lim_(x→+∞) f(x)=0$
$1) w e h a v e f (x) = \int_{x}^{x^{2} + 3} e^{- x t} l n (1 + e^{- x t}) d t (x > 0) c h a n g e m e n t$ $x t = u g i v e f (x) = \frac{1}{x} \int_{x^{2}}^{x^{3} + 3 x} e^{- u} l n (1 + e^{- u}) d u \Rightarrow$ $x f (x) = \int_{x^{2}}^{x^{3} + 3 x} e^{- u} l n (1 + e^{- u}) d y =_{b y p s r t s} {[- e^{- u} l n (1 + e^{- u})]}_{x^{2}}^{x^{3} + 3 x}$ $- \int_{x^{2}}^{x^{3} + 3 x} (- e^{- u}) \times \frac{- e^{- u}}{1 + e^{- u}} d u = e^{- x^{2}} l n (1 + e^{- x^{2}})$ $- e^{- (x^{3} + 3 x)} l n (1 + e^{- (x^{3} + 3 x)}) + \int_{x^{2}}^{x^{3} + 3 x} \frac{e^{- 2 u}}{1 + e^{- u}} d u w e h a v e$ $\int_{x^{2}}^{x^{3} + 3 x} \frac{e^{- 2 u}}{1 + e^{- u}} d u = \int_{x^{2}}^{x^{3} + 3 x} \frac{1}{e^{2 u} + e^{u}} d u =_{e^{u} = z} \int_{e^{x^{2}}}^{e^{x^{3} + 3 x}} \frac{1}{z^{2} + z} \frac{d z}{z}$ $= \int_{e^{x^{2}}}^{e^{x^{3} + 3 x}} \frac{d z}{z^{2} (z + 1)} d e c o m p o s i t i o n o f F (z) = \frac{1}{z^{2} (z + 1)}$ $F (z) = \frac{a}{z} + \frac{b}{z^{2}} + \frac{c}{z + 1}$ $b = 1, c = 1 \Rightarrow F (z) = \frac{a}{z} + \frac{1}{z^{2}} + \frac{1}{z + 1}$ ${l i m}_{z \to + \infty} z F (z) = 0 = a + c \Rightarrow a = - c = - 1 \Rightarrow F (z) = - \frac{1}{z} + \frac{1}{z^{2}} + \frac{1}{z + 1}$ $\int_{e^{x^{2}}}^{e^{x^{3} + 3 x}} \frac{d z}{z^{2} (z + 1)} = {[l n ∣ \frac{z + 1}{z} ∣]}_{e^{x^{2}}}^{e^{x^{3} + 3 x}} + {[- \frac{1}{z}]}_{e^{x^{2}}}^{e^{x^{3} + 3 x}}$ $= l n (\frac{1 + e^{x^{3} + 3 x}}{e^{x^{3} + 3 x}}) - l n (\frac{1 + e^{x^{2}}}{e^{x^{2}}}) + (e^{- x^{2}} - e^{- (x^{3} + 3 x)}) \Rightarrow$ $f (x) = \frac{1}{x} {e^{- x^{2}} l n (1 + e^{- x^{2}}) - e^{- (x^{3} + 3 x)} l n (1 + e^{- (x^{3} + 3 x)})$ $l n (\frac{1 + e^{x^{3} + 3 x}}{e^{x^{3} + 3 x}}) - l n (\frac{1 + e^{x^{2}}}{e^{x^{2}}}) + e^{- x^{2}} - e^{- (x^{3} + 3 x)}}$ $2) {l i m}_{x \to + \infty} f (x) = 0$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum