
Question and Answers Forum
Question Number 65287 by mathmax by abdo last updated on 27/Jul/19
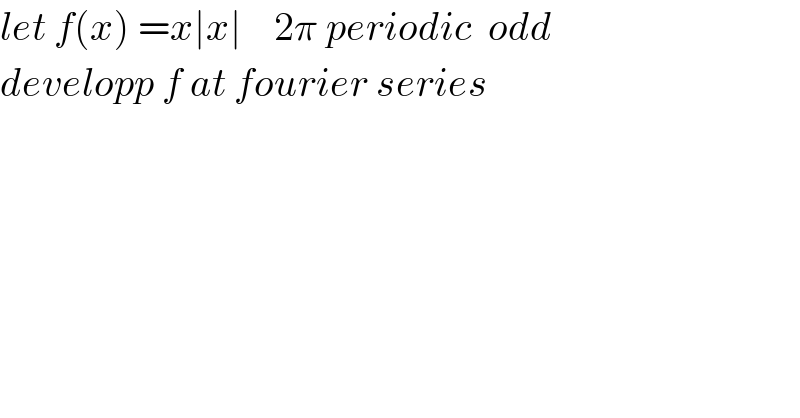
Commented by mathmax by abdo last updated on 28/Jul/19
![f(x) =Σ_(n=1) ^∞ a_n sin(nx) with a_n =(2/T) ∫_([T]) f(x)sin(nx)dx =(2/(2π)) ∫_(−π) ^π x∣x∣ sin(nx)dx =(2/π) ∫_0 ^π x^2 sin(nx)dx ⇒ (π/2)a_n =∫_0 ^π x^2 sin(nx)dx by parts u =x^2 and v^′ =sin(nx) ⇒ (π/2)a_n =[−(x^2 /n)cos(nx)]_0 ^π −∫_0 ^π (2x)(−(1/n))cos(nx)dx =−(π^2 /n)(−1)^n +(2/n) ∫_0 ^π x cos(nx)dx again by parts ∫_0 ^π x cos(nx)dx =[(x/n)sin(nx)]_0 ^π −∫_0 ^π (1/n)sin(nx)dx =−(1/n) ∫_0 ^π sin(nx)dx =(1/n^2 )[cos(nx)]_0 ^π =(1/n^2 )((−1)^n −1) ⇒ (π/2)a_n =−(π^2 /n)(−1)^n +(2/n^3 ) {(−1)^n −1} a_n =(2/π){−(π^2 /n)(−1)^n +(2/n^3 ){ (−1)^n −1)} =−2π (((−1)^n )/n) +(4/(πn^3 )){ (−1)^n −1} ⇒ x∣x∣ =Σ_(n=1) ^∞ (−2π (((−1)^n )/n) +(4/(πn^3 )){(−1)^n −1})sin(nx) =−2π Σ_(n=1) ^∞ (((−1)^n )/n)sin(nx) +(4/π) Σ_(n=1) ^∞ (((−1)^n −1)/n^3 )sin(nx)](Q65338.png)
| ||
Question and Answers Forum | ||
Question Number 65287 by mathmax by abdo last updated on 27/Jul/19 | ||
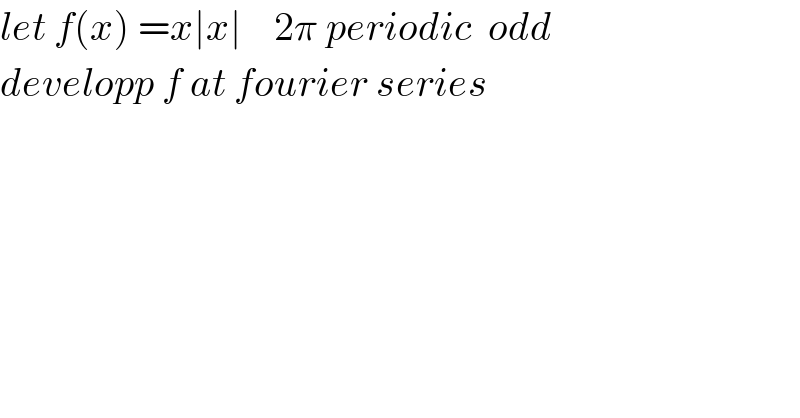 | ||
Commented by mathmax by abdo last updated on 28/Jul/19 | ||
![f(x) =Σ_(n=1) ^∞ a_n sin(nx) with a_n =(2/T) ∫_([T]) f(x)sin(nx)dx =(2/(2π)) ∫_(−π) ^π x∣x∣ sin(nx)dx =(2/π) ∫_0 ^π x^2 sin(nx)dx ⇒ (π/2)a_n =∫_0 ^π x^2 sin(nx)dx by parts u =x^2 and v^′ =sin(nx) ⇒ (π/2)a_n =[−(x^2 /n)cos(nx)]_0 ^π −∫_0 ^π (2x)(−(1/n))cos(nx)dx =−(π^2 /n)(−1)^n +(2/n) ∫_0 ^π x cos(nx)dx again by parts ∫_0 ^π x cos(nx)dx =[(x/n)sin(nx)]_0 ^π −∫_0 ^π (1/n)sin(nx)dx =−(1/n) ∫_0 ^π sin(nx)dx =(1/n^2 )[cos(nx)]_0 ^π =(1/n^2 )((−1)^n −1) ⇒ (π/2)a_n =−(π^2 /n)(−1)^n +(2/n^3 ) {(−1)^n −1} a_n =(2/π){−(π^2 /n)(−1)^n +(2/n^3 ){ (−1)^n −1)} =−2π (((−1)^n )/n) +(4/(πn^3 )){ (−1)^n −1} ⇒ x∣x∣ =Σ_(n=1) ^∞ (−2π (((−1)^n )/n) +(4/(πn^3 )){(−1)^n −1})sin(nx) =−2π Σ_(n=1) ^∞ (((−1)^n )/n)sin(nx) +(4/π) Σ_(n=1) ^∞ (((−1)^n −1)/n^3 )sin(nx)](Q65338.png) | ||