
Question and Answers Forum
Question Number 28071 by abdo imad last updated on 20/Jan/18
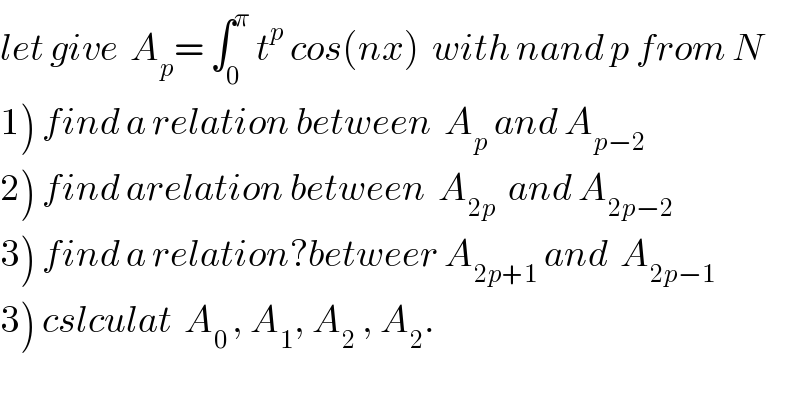
Commented by abdo imad last updated on 26/Jan/18
![let integrate by parts 1)A_p = [(1/n)t^p sin(nt)]_0 ^π − ∫_0 ^π (p/n)t^(p−1) sin(nt)dx =−(p/n) ∫_0 ^π t^(p−1) sin(nt)dt =−(p/n)( [((−1)/n) t^(p−1) cos(nt)]_0 ^π −∫_0 ^π −((p−1)/n) t^(p−2) cos(nt)dt ) =−(p/n)( ((−π^(p−1) (−1)^n )/n) +((p−1)/n) ∫_0 ^π t^(p−2) cos(nt)dt) =(p/n^2 ) π^(p−1) (−1)^n −((p(p−1))/n^2 ) A_(p−2) so A_p = (1/n^2 )( p π^(p−1) (−1)^n −p(p−1) A_(p−2)) ) 2) A_(2p) = (1/n^2 )(2p π^(2p−1) (−1)^n −(2p)(2p−1) A_(2p−2) ) 3) A_(2p+1 ) ^( ) = (1/n^(2 ) )((2p+1)π^(2p) (−1)^n −2p(2p+1) A_(2p−1) ) 4) A_0 = ∫_0 ^π cos(nx)dx=[(1/n) sin(nx)]_0 ^π =0 A_1 = ∫_0 ^π t cos(nt)t = [ (t/n) sin(nt)]_0 ^π − ∫_0 ^π (1/n)sin(nt)dt = −(1/n) ∫_0 ^π sin(nt)dt= (1/n^2 )[ cos(nt)]_0 ^π =(1/n^2 )( (−1)^n −1) A_(2 ) =(1/n^2 )( 2π(−1)^n −2A_0 ) =((2π)/n^2 )(−1)^n ....be contunued...](Q28478.png)
Commented by abdo imad last updated on 26/Jan/18
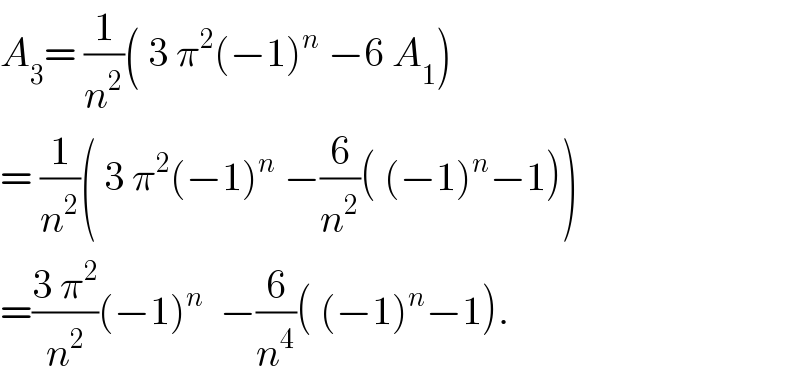
Commented by abdo imad last updated on 26/Jan/18
| ||
Question and Answers Forum | ||
Question Number 28071 by abdo imad last updated on 20/Jan/18 | ||
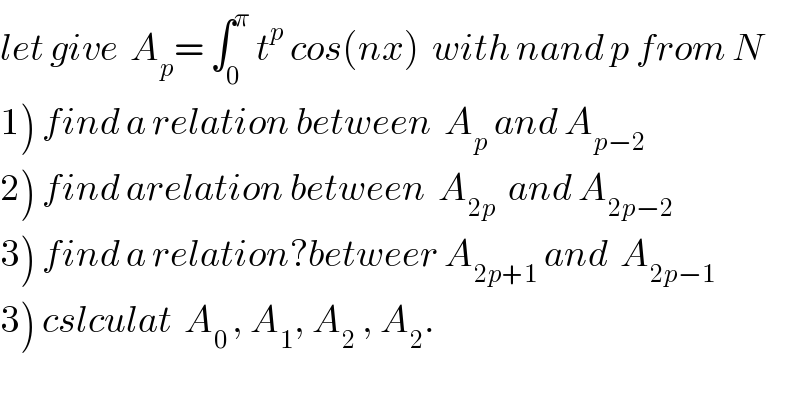 | ||
Commented by abdo imad last updated on 26/Jan/18 | ||
![let integrate by parts 1)A_p = [(1/n)t^p sin(nt)]_0 ^π − ∫_0 ^π (p/n)t^(p−1) sin(nt)dx =−(p/n) ∫_0 ^π t^(p−1) sin(nt)dt =−(p/n)( [((−1)/n) t^(p−1) cos(nt)]_0 ^π −∫_0 ^π −((p−1)/n) t^(p−2) cos(nt)dt ) =−(p/n)( ((−π^(p−1) (−1)^n )/n) +((p−1)/n) ∫_0 ^π t^(p−2) cos(nt)dt) =(p/n^2 ) π^(p−1) (−1)^n −((p(p−1))/n^2 ) A_(p−2) so A_p = (1/n^2 )( p π^(p−1) (−1)^n −p(p−1) A_(p−2)) ) 2) A_(2p) = (1/n^2 )(2p π^(2p−1) (−1)^n −(2p)(2p−1) A_(2p−2) ) 3) A_(2p+1 ) ^( ) = (1/n^(2 ) )((2p+1)π^(2p) (−1)^n −2p(2p+1) A_(2p−1) ) 4) A_0 = ∫_0 ^π cos(nx)dx=[(1/n) sin(nx)]_0 ^π =0 A_1 = ∫_0 ^π t cos(nt)t = [ (t/n) sin(nt)]_0 ^π − ∫_0 ^π (1/n)sin(nt)dt = −(1/n) ∫_0 ^π sin(nt)dt= (1/n^2 )[ cos(nt)]_0 ^π =(1/n^2 )( (−1)^n −1) A_(2 ) =(1/n^2 )( 2π(−1)^n −2A_0 ) =((2π)/n^2 )(−1)^n ....be contunued...](Q28478.png) | ||
Commented by abdo imad last updated on 26/Jan/18 | ||
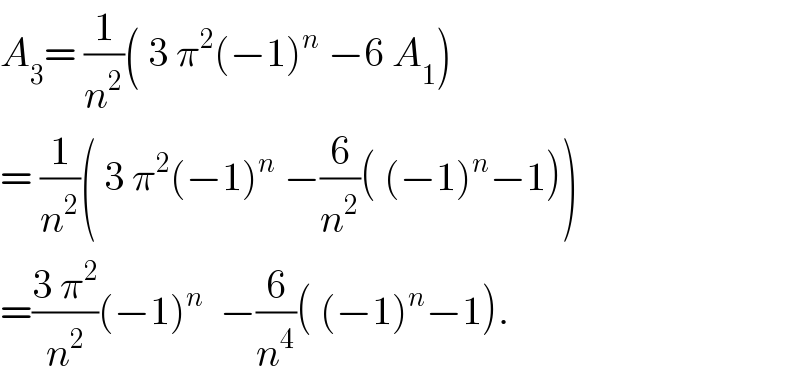 | ||
Commented by abdo imad last updated on 26/Jan/18 | ||
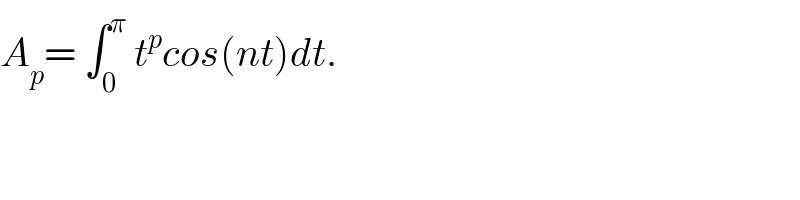 | ||