
Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 33847 by prof Abdo imad last updated on 26/Apr/18
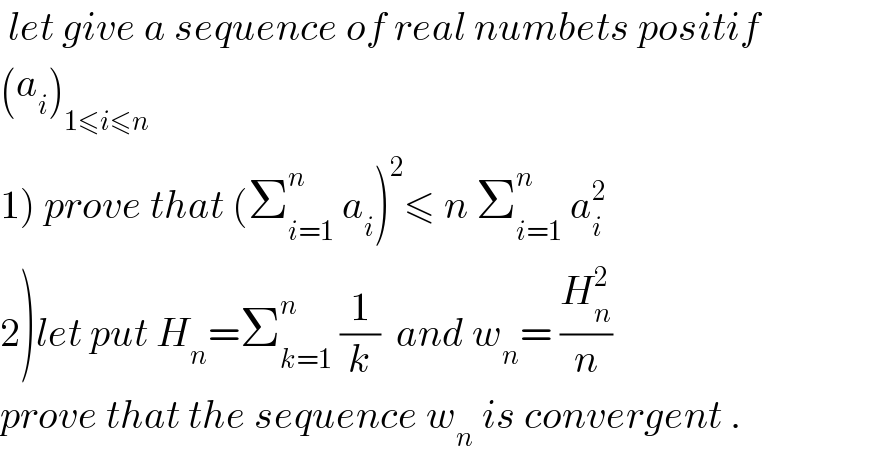
Commented by prof Abdo imad last updated on 27/Apr/18
![for all sequences of reals numbers positifs (a_i )_(1≤i≤n) and (b_i )_(1≤i≤n) we have Σ_(i=1) ^n a_i b_i ≤ (Σ_(i=1) ^n a_i ^2 )^(1/2) (Σ_(i=1) ^n b_i ^2 )^(1/2) (holder inequality) let take b_i =1 ∀i∈[[1,n]] ⇒Σ_(i=1) ^n a_i ≤(√n) (Σ_(i=1) ^n a_i ^2 )^(1/2) ⇒ (Σ_(i=1) ^n a_i )^2 ≤n(Σ_(i=1) ^n a_i ^2 ) 2)let take a_i = (1/i) ∀i∈[1,n] ⇒(Σ_(i=1) ^n (1/i))^2 ≤nΣ_(i=1) ^n (1/i^2 ) ⇒ H_n ^2 ≤ n Σ_(i=1) ^n (1/i^2 ) ⇒ (H_n ^2 /n) ≤ Σ_(i=1) ^n (1/i^2 ) ⇒ w_n ≤ Σ_(i=1) ^n (1/i^2 ) Rieman serie convergent so (w_n ) is convergent.](Q33920.png)
| ||
Question and Answers Forum | ||
Previous in Relation and Functions Next in Relation and Functions | ||
Question Number 33847 by prof Abdo imad last updated on 26/Apr/18 | ||
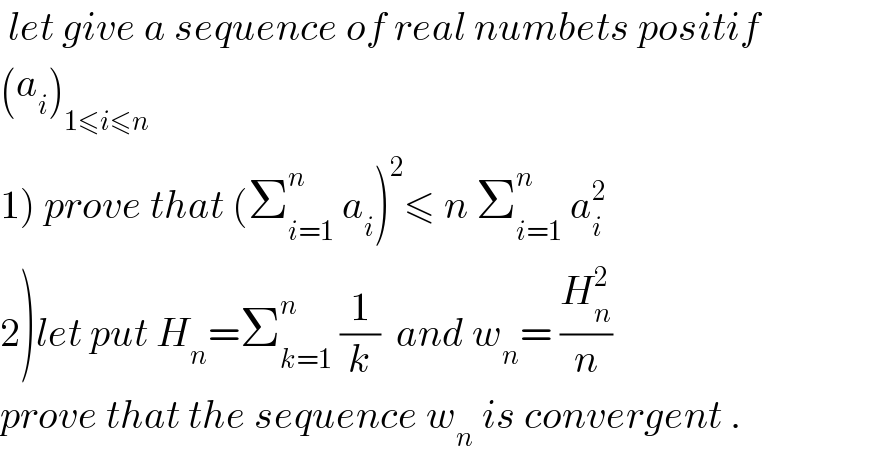 | ||
Commented by prof Abdo imad last updated on 27/Apr/18 | ||
![for all sequences of reals numbers positifs (a_i )_(1≤i≤n) and (b_i )_(1≤i≤n) we have Σ_(i=1) ^n a_i b_i ≤ (Σ_(i=1) ^n a_i ^2 )^(1/2) (Σ_(i=1) ^n b_i ^2 )^(1/2) (holder inequality) let take b_i =1 ∀i∈[[1,n]] ⇒Σ_(i=1) ^n a_i ≤(√n) (Σ_(i=1) ^n a_i ^2 )^(1/2) ⇒ (Σ_(i=1) ^n a_i )^2 ≤n(Σ_(i=1) ^n a_i ^2 ) 2)let take a_i = (1/i) ∀i∈[1,n] ⇒(Σ_(i=1) ^n (1/i))^2 ≤nΣ_(i=1) ^n (1/i^2 ) ⇒ H_n ^2 ≤ n Σ_(i=1) ^n (1/i^2 ) ⇒ (H_n ^2 /n) ≤ Σ_(i=1) ^n (1/i^2 ) ⇒ w_n ≤ Σ_(i=1) ^n (1/i^2 ) Rieman serie convergent so (w_n ) is convergent.](Q33920.png) | ||