
Question and Answers Forum
Question Number 34222 by abdo imad last updated on 03/May/18

Commented by candre last updated on 03/May/18
![J_n =∫_0 ^∞ x^n e^(−(x^2 /2)) dx u=x^(n−1) ⇒du=(n−1)x^(n−2) dx dv=xe^(−(x^2 /2)) dx⇒v=−e^(−(x^2 /2)) =−[x^(n−1) e^(−(x^2 /2)) ]_0 ^∞ +(n−1)∫x^(n−2) e^(−(x^2 /2)) dx =(n−1)J_(n−2) ∫xe^(−(x^2 /2)) dx=−∫e^u du=−e^u =−e^(−(x^2 /2)) u=−(x^2 /2)⇒du=−xdx](Q34245.png)
Commented by candre last updated on 03/May/18
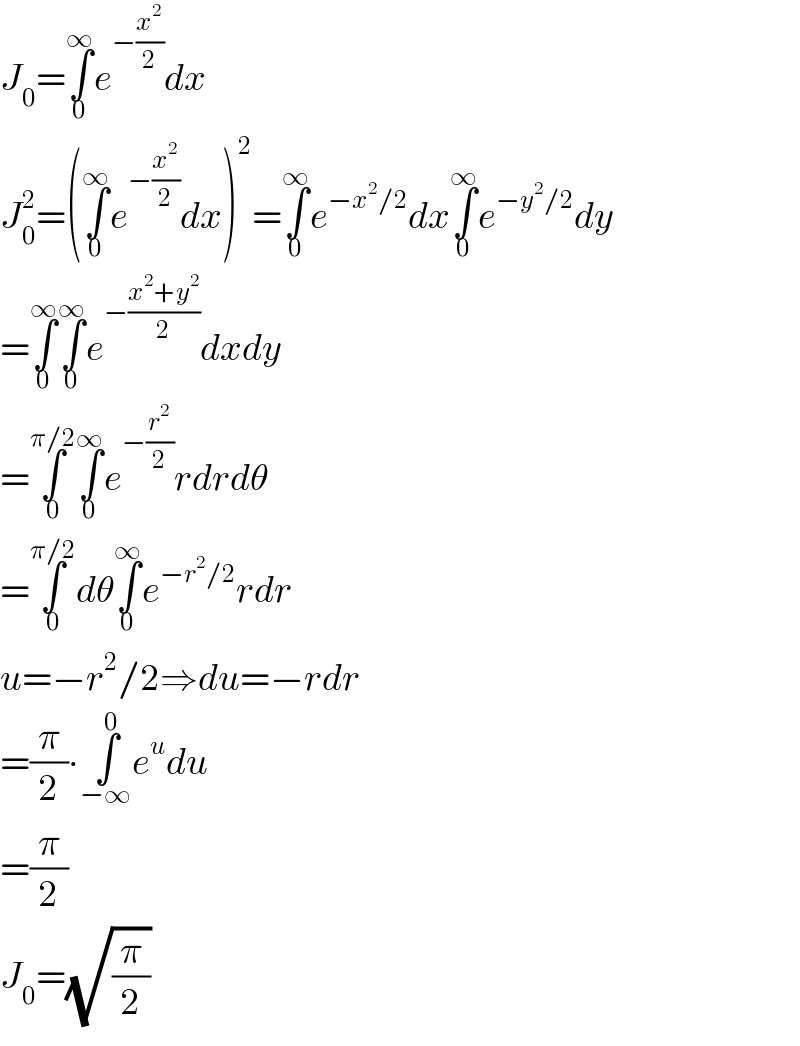
Commented by candre last updated on 03/May/18
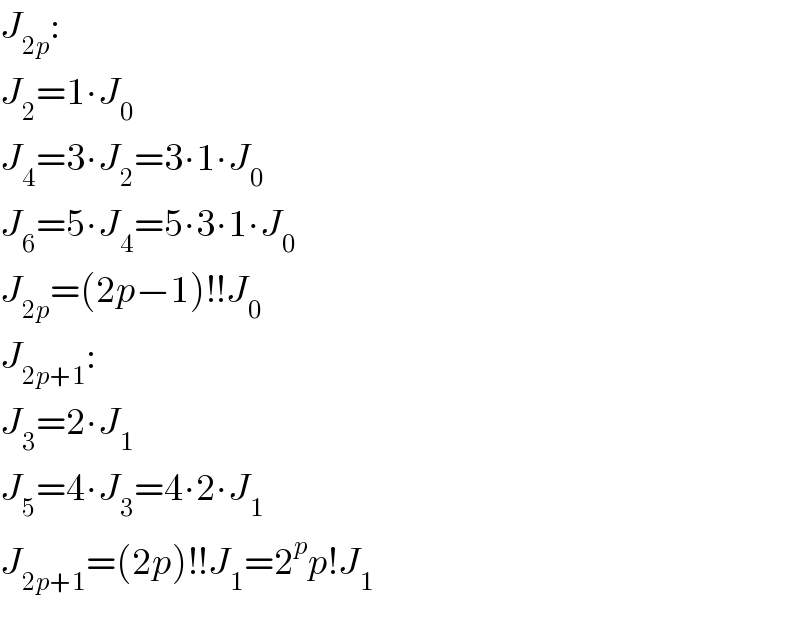
Commented by abdo mathsup 649 cc last updated on 05/May/18
![1) let prove that J_(n+1) = nJ_(n−1) J_(n+1) = ∫_0 ^∞ x^(n+1) e^(−(x^2 /2)) dx =−∫_0 ^∞ x^n (−xe^(−(x^2 /2)) dx) =−([ x^n e^(−(x^2 /2)) ]_0 ^(+∞) −∫_0 ^∞ n x^(n−1) e^(−(x^2 /2)) dx) = n ∫_0 ^∞ x^(n−1) e^(−(x^2 /2)) dx = n J_(n−1) ⇒ J_n =(n−1)J_(n−2) ∀n≥2 2) J_(2p) = (2p−1)J_(2p−2) ⇒ Π_(p=1) ^n J_(2p) =Π_(p=1) ^n J_(2p−2) Π_(p=1) ^n (2p−1)⇒ J_2 .J_4 .....J_(2n) =1.3.5....(2n−1) J_0 .J_2 ....J_(2n−2) ⇒ J_(2n) =1.3.5....(2n−1) J_0 =((1.2.3.4......(2n−1)(2n))/(2^n n!)) J_0 =(((2n)!)/(2^n (n!))) J_0 J_0 = ∫_0 ^∞ e^(−(x^2 /2)) dx =_((√2) t=x) ∫_0 ^∞ e^(−t^2 ) (√2)dt = (√2) ((√π)/2) =(√(π/2)) ⇒ J_(2n) = (((2n)!)/(2^n n!)) (√(π/2)) J_(2p+1) = 2p J_(2p−1 ) ⇒ Π_(p=1) ^n J_(2p+1) = Π_(p=1) ^n (2p) Π_(p=1) ^n J_(2p−1) ⇒ J_3 .J_5 .....J_(2n+1) =2^n n! J_1 .J_3 ....J_(2n−1) ⇒ J_(2n+1) = 2^n n! J_1 J_1 = ∫_0 ^∞ x e^(−(x^2 /2)) dx =−∫_0 ^∞ (−x) e^(−(x^2 /2)) dx =−[ e^(−(x^2 /2)) ]_0 ^(+∞) = 1 ⇒ J_(2n+1) = 2^n (n!) .](Q34351.png)
