Question and Answers Forum
Question Number 42195 by math khazana by abdo last updated on 20/Aug/18
![let p(x)=x^(10) −1 1) find roots of p(x) 2) factorize i nside C[x] p(x{ 3) factorize inside R[x] p(x) .](Q42195.png)
Answered by maxmathsup by imad last updated on 21/Aug/18
![1) p(z)=0 ⇔ z^(10) −1=0 ⇔ z^(10) =1 if z=r e^(iθ) we get r^(10) e^(i10θ) =e^(i2kπ) ⇒ r =1 and θ =((2kπ)/(10)) =((kπ)/5) so the roots of p(x)are z_k =e^(i((kπ)/5)) with k∈[[0,9]] 2) p(x) =Π_(k=0) ^9 (x−z_k ) =Π_(k=0) ^9 (x−e^((ikπ)/5) ) 3) generally let decmpose q(x) =x^(2n) −1 the roots are z_k =e^((ikn)/n) with k ∈[[0,2n−1]] ⇒q(x)=Π_(k=0) ^(2n−1) (x−e^((ikπ)/n) ) but z_0 =1 z_1 =e^((iπ)/n) z_2 =e^((i2π)/n) z_(n−1) =e^((i(n−1)π)/n) z_n =−1 z_(n+1) =e^((i(n+1)π)/n) ...z_(2n−1) =e^((i(2n−1)π)/n) ⇒z_1 ^− =e^(−((iπ)/n)) =e^(2iπ−((iπ)/n)) = e^(i(((2n−1)π)/n)) =z_(2n−1) ^− .....⇒z_(2n−p) =z_p ^− ⇒ q(x) =(x^2 −1) Π_(k=1) ^(n−1) (x−z_k )(x−z_k ^− )=(x^2 −1)Π_(k=1) ^(n−1) (x^2 −2cos(((kπ)/n))x +1) for n=5 we get p(x)=(x^2 −1)Π_(k=1) ^4 (x^2 −2cos(((kπ)/5))x +1) =(x^2 −1)(x^2 −2cos((π/5))x +1)(x^2 −2cos(((2π)/5))x+1)(x^2 −2cos(((3π)/5))x+1)(x^2 −2cos(((4π)/5))x+1). =(x^2 −2cos((π/5))x+1)(x^2 +2cos((π/5))x+1)(x^2 −2cos(((2π)/5))x+1)(x^2 +2cos(((2π)/5))x+1).](Q42283.png)
Commented by maxmathsup by imad last updated on 21/Aug/18
| ||
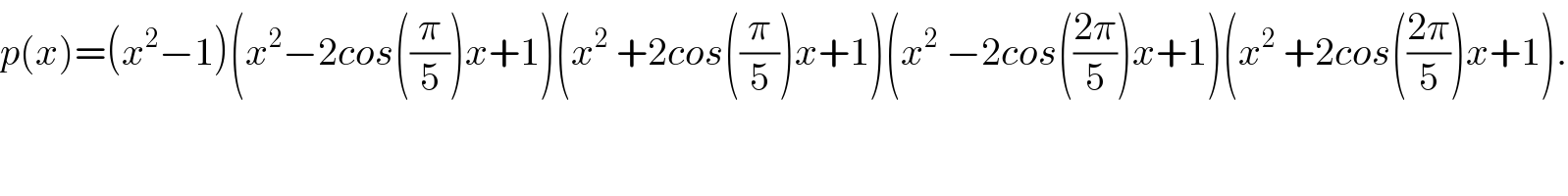
Question and Answers Forum | ||
| ||
Question Number 42195 by math khazana by abdo last updated on 20/Aug/18 | ||
| ||
Answered by maxmathsup by imad last updated on 21/Aug/18 | ||
| ||
| ||
Commented by maxmathsup by imad last updated on 21/Aug/18 | ||
| ||
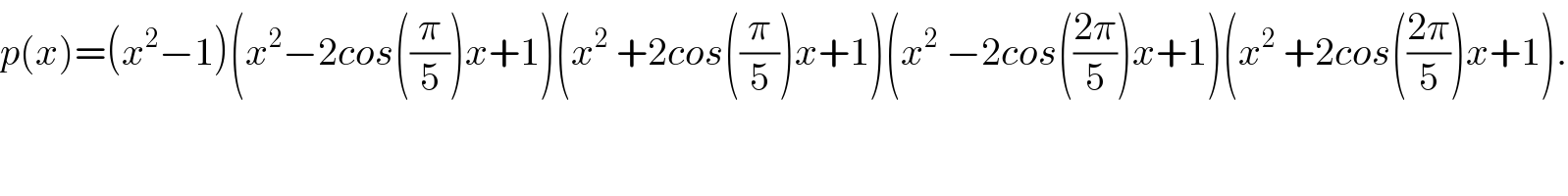