Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 175624 by infinityaction last updated on 04/Sep/22

$$\mathrm{let}\mathrm{p}\left(\mathrm{x}\right)={\mathrm{x}}^6+{\mathrm{ax}}^5+{\mathrm{bx}}^4+{\mathrm{cx}}^3+{\mathrm{dx}}^2+\mathrm{ex}+\mathrm{f}$$$$\mathrm{be}\mathrm{a}\mathrm{polynomial}\mathrm{function}\mathrm{such}$$$$\mathrm{that}\mathrm{p}\left(1\right)=1;\mathrm{p}\left(2\right)=2;\mathrm{p}\left(3\right)=3$$$$\mathrm{p}\left(4\right)=4;\mathrm{p}\left(5\right)=5;\mathrm{p}\left(6\right)=6\mathrm{then}$$$$\mathrm{find}\mathrm{p}\left(7\right)=?$$

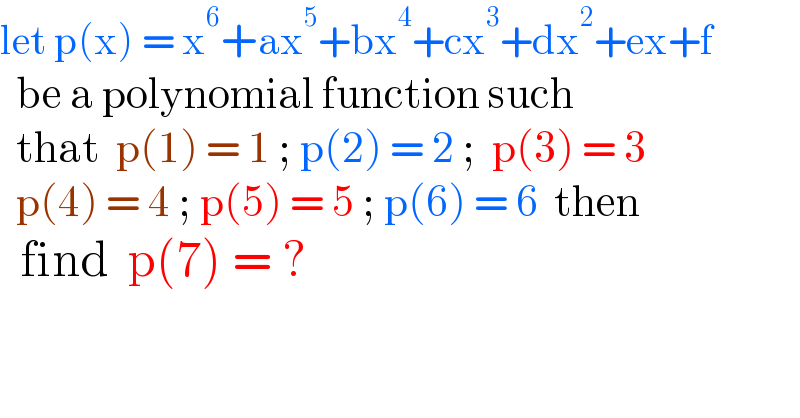
Answered by cortano1 last updated on 04/Sep/22

$$\mathrm{p}\left(\mathrm{x}\right)=(\mathrm{x}-1)(\mathrm{x}-2)(\mathrm{x}-3)(\mathrm{x}-4)(\mathrm{x}-5)(\mathrm{x}-6)+\mathrm{x}$$$$\mathrm{p}\left(7\right)=6.5.4.3.2.1+7=6!+7$$$$=727$$

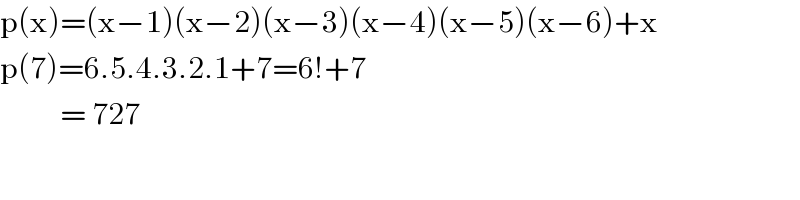
Commented by BaliramKumar last updated on 05/Sep/22

$$\mathrm{p}\left(\mathrm{n}\right)=?[n>6]$$

Answered by leodera last updated on 04/Sep/22

$$$$$$p\left(x\right)=(x-1)(x-2)(x-3)(x-4)(x-5)(\mathit{x}-6)+\mathit{x}$$$$\mathit{p}\left(7\right)=6!+7=720+7=727$$

Answered by floor(10²Eta[1]) last updated on 04/Sep/22

$$\mathrm{p}\left(1\right)=1\Rightarrow \mathrm{p}\left(\mathrm{x}\right)=(\mathrm{x}-1)\mathrm{a}\left(\mathrm{x}\right)+1$$$$\mathrm{p}\left(2\right)=\mathrm{a}\left(2\right)+1=2\Rightarrow \mathrm{a}\left(2\right)=1\Rightarrow \mathrm{a}\left(\mathrm{x}\right)=(\mathrm{x}-2)\mathrm{b}\left(\mathrm{x}\right)+1$$$$\mathrm{p}\left(\mathrm{x}\right)=(\mathrm{x}-1)((\mathrm{x}-2)\mathrm{b}\left(\mathrm{x}\right)+1)+1$$$$\mathrm{p}\left(3\right)=2(\mathrm{b}\left(3\right)+1)+1=3\Rightarrow \mathrm{b}\left(3\right)=0\Rightarrow \mathrm{b}\left(\mathrm{x}\right)=(\mathrm{x}-3)\mathrm{c}\left(\mathrm{x}\right)$$$$\mathrm{p}\left(\mathrm{x}\right)=(\mathrm{x}-1)((\mathrm{x}-2)(\mathrm{x}-3)\mathrm{c}\left(\mathrm{x}\right)+1)+1$$$$\mathrm{p}\left(4\right)=3(2\mathrm{c}\left(4\right)+1)+1=4\Rightarrow \mathrm{c}\left(4\right)=0\Rightarrow \mathrm{c}\left(\mathrm{x}\right)=(\mathrm{x}-4)\mathrm{d}\left(\mathrm{x}\right)$$$$\Rightarrow \mathrm{p}\left(\mathrm{x}\right)=(\mathrm{x}-1)[(\mathrm{x}-2)(\mathrm{x}-3)(\mathrm{x}-4)\mathrm{d}\left(\mathrm{x}\right)+1)+1$$$$\mathrm{p}\left(5\right)=4[3.2\mathrm{d}\left(5\right)+1]+1=5\Rightarrow \mathrm{d}\left(5\right)=0\Rightarrow \mathrm{d}\left(\mathrm{x}\right)=(\mathrm{x}-5)\mathrm{e}\left(\mathrm{x}\right)$$$$\mathrm{p}\left(\mathrm{x}\right)=(\mathrm{x}-1)[(\mathrm{x}-2)(\mathrm{x}-3)(\mathrm{x}-4)(\mathrm{x}-5)\mathrm{e}\left(\mathrm{x}\right)+1]+1$$$$\mathrm{p}\left(6\right)=5[4.3.2\mathrm{e}\left(6\right)+1]+1=6\Rightarrow \mathrm{e}\left(6\right)=0\Rightarrow \mathrm{e}\left(\mathrm{x}\right)=(\mathrm{x}-6)\mathrm{C}$$$$\Rightarrow \mathrm{p}\left(\mathrm{x}\right)=(\mathrm{x}-1)[(\mathrm{x}-2)(\mathrm{x}-3)(\mathrm{x}-4)(\mathrm{x}-5)(\mathrm{x}-6)\mathrm{C}+1]+1$$$$=(\mathrm{x}-1)(\mathrm{x}-2)(\mathrm{x}-3)(\mathrm{x}-4)(\mathrm{x}-5)(\mathrm{x}-6)\mathrm{C}+\mathrm{x}$$$$\mathrm{p}\left(7\right)=6!\mathrm{C}+7=720\mathrm{C}+7,\mathrm{C}\in {\mathbb{R}}^{\ast }$$$$\mathrm{but}\mathrm{C}=1\mathrm{because}\mathrm{p}\left(\mathrm{x}\right)={\mathrm{x}}^6+{\mathrm{ax}}^5+...$$$$\Rightarrow \mathrm{p}\left(7\right)=727$$

Commented by infinityaction last updated on 04/Sep/22

$$thankssir$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com