
Question and Answers Forum
Question Number 27974 by abdo imad last updated on 18/Jan/18
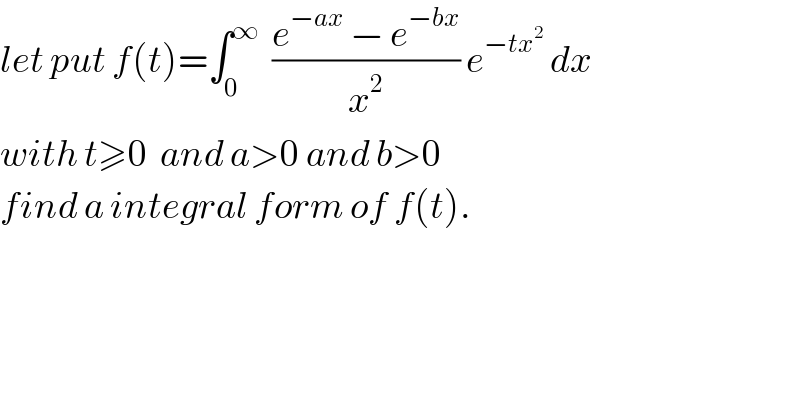
Commented by abdo imad last updated on 20/Jan/18
![after verifying that f is derivable on ]0,+∞[ we have f^, (t)= −∫_0 ^∞ ( e^(−ax) −e^(−bx) )e^(−tx^2 ) dx =∫_0 ^∞ e^(−tx^2 −bx) dx −∫_0 ^∞ e^(−tx^2 −ax) dx but ∫_0 ^∞ e^(−tx^2 −ax) dx = ∫_0 ^∞ e^(−( ((√t)x)^2 +2(a/(2(√t)))((√t)x) + (a^2 /(4t)) −(a^2 /(4t)))) dx = e^(a^2 /(4t)) ∫_0 ^∞ e^(−((√t)x +(a/(√t)))^2 ) dx the ch. (√t)x +(a/(√t))=u give ∫_0 ^∞ e^(−tx^2 −ax) dx = e^(a^2 /(4t)) ∫_(a/(√t)) ^(+∞) e^(−u^2 ) (du/(√t)) = (1/(√t)) e^(a^2 /(4t)) ( ∫_0 ^∞ e^(−u^2 ) du − ∫_0 ^(a/(√t)) e^(−u^2 ) du) = (1/(√t)) e^(a^2 /(4t)) ( ((√π)/2) − ∫_0 ^(a/(√t)) e^(−u^2 ) du) and by the same manner we get ∫_0 ^∞ e^(−tx^2 −bx) dx = (1/(√t)) e^(b^2 /(4t)) ( ((√π)/2) − ∫_0 ^(b/(√t)) e^(−u^2 ) du) f^′ (t)= ((√π_ )/(2(√t)))( e^(b^2 /(4t)) − e^(a^2 /(4t)) ) + ∫_0 ^(a/(√t)) e^(−u^2 ) du −∫_0 ^(b/(√t)) e^(−u^2 ) du = ((√π)/(2(√t))) ( e^(b^2 /(4t)) − e^(a^2 /(4t)) ) −∫_(a/(√t)) ^(b/(√t)) e^(−u^2 ) du = ψ(t) ⇒ f(t)= ∫_. ^t ψ(u)du +λ .](Q28135.png)
| ||
Question and Answers Forum | ||
Question Number 27974 by abdo imad last updated on 18/Jan/18 | ||
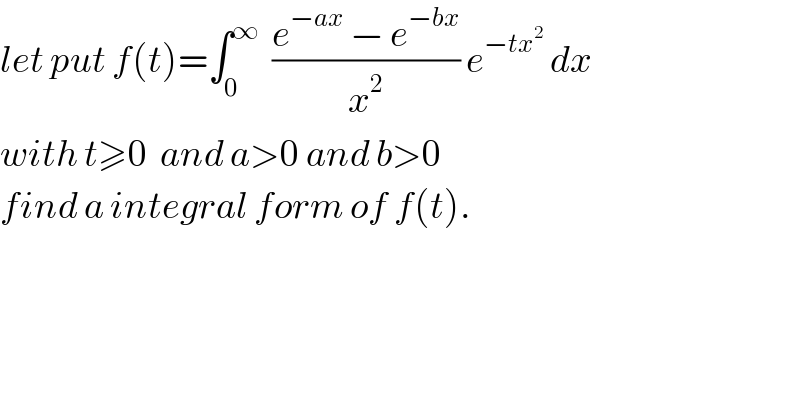 | ||
Commented by abdo imad last updated on 20/Jan/18 | ||
![after verifying that f is derivable on ]0,+∞[ we have f^, (t)= −∫_0 ^∞ ( e^(−ax) −e^(−bx) )e^(−tx^2 ) dx =∫_0 ^∞ e^(−tx^2 −bx) dx −∫_0 ^∞ e^(−tx^2 −ax) dx but ∫_0 ^∞ e^(−tx^2 −ax) dx = ∫_0 ^∞ e^(−( ((√t)x)^2 +2(a/(2(√t)))((√t)x) + (a^2 /(4t)) −(a^2 /(4t)))) dx = e^(a^2 /(4t)) ∫_0 ^∞ e^(−((√t)x +(a/(√t)))^2 ) dx the ch. (√t)x +(a/(√t))=u give ∫_0 ^∞ e^(−tx^2 −ax) dx = e^(a^2 /(4t)) ∫_(a/(√t)) ^(+∞) e^(−u^2 ) (du/(√t)) = (1/(√t)) e^(a^2 /(4t)) ( ∫_0 ^∞ e^(−u^2 ) du − ∫_0 ^(a/(√t)) e^(−u^2 ) du) = (1/(√t)) e^(a^2 /(4t)) ( ((√π)/2) − ∫_0 ^(a/(√t)) e^(−u^2 ) du) and by the same manner we get ∫_0 ^∞ e^(−tx^2 −bx) dx = (1/(√t)) e^(b^2 /(4t)) ( ((√π)/2) − ∫_0 ^(b/(√t)) e^(−u^2 ) du) f^′ (t)= ((√π_ )/(2(√t)))( e^(b^2 /(4t)) − e^(a^2 /(4t)) ) + ∫_0 ^(a/(√t)) e^(−u^2 ) du −∫_0 ^(b/(√t)) e^(−u^2 ) du = ((√π)/(2(√t))) ( e^(b^2 /(4t)) − e^(a^2 /(4t)) ) −∫_(a/(√t)) ^(b/(√t)) e^(−u^2 ) du = ψ(t) ⇒ f(t)= ∫_. ^t ψ(u)du +λ .](Q28135.png) | ||