
Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 42190 by maxmathsup by imad last updated on 19/Aug/18
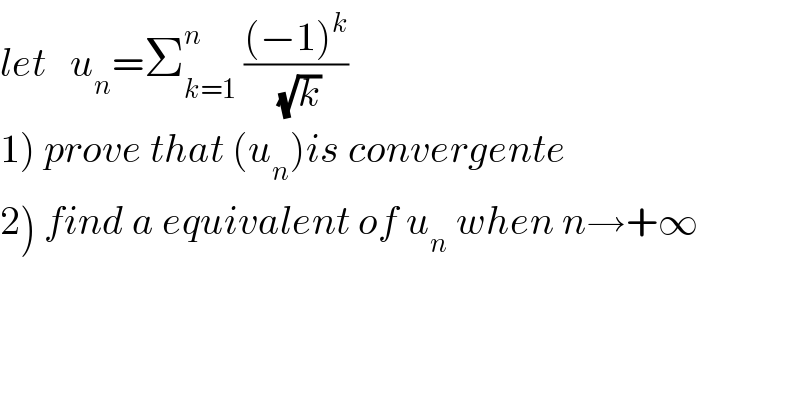
Commented by maxmathsup by imad last updated on 21/Aug/18
![1) we have lim_(n→+∞) u_n = Σ_(k=1) ^∞ (((−1)^k )/(√k)) and this serie is convergente (alternate serie) 2) we have u_n =Σ_(p=1) ^([(n/2)]) (1/(√(2p))) −Σ_(p=0) ^([((n−1)/2)]) (1/(√(2p+1))) = Σ v_p −Σw_p (v_p )is decreasing ⇒ ∫_p ^(p+1) (dx/(√(2x))) ≤ v_p ≤ ∫_(p−1) ^p (dx/(√(2x))) ⇒ Σ_(p=1) ^([(n/2)]) ∫_p ^(p+1) (dx/(√(2x))) ≤ Σ_(p=1) ^([(n/2)]) v_p ≤ Σ_(p=1) ^([(n/2)]) ∫_(p−1) ^p (dx/(√(2x))) ⇒ ∫_1 ^([(n/2)] +1) (dx/(√(2x))) ≤ Σ_(p=1) ^([(n/2)]) v_p ≤ ∫_0 ^([(n/2)]) (dx/(√(2x))) ⇒ (1/(√2))[2(√x)]_1 ^([(n/2)]+1) ≤ Σ_(p=1) ^([(n/2)]) v_p ≤(1/(√2))[2(√x)]_0 ^([(n/2)]) ⇒ (√2){(√([(n/2)]+1))−1}≤Σ v_p ≤(√2)(√([(n/2)])) also (w_p ) is decreasing ⇒ ∫_p ^(p+1) (dx/(√(2x+1))) ≤ w_p ≤ ∫_(p−1) ^p (dx/(√(2x+1))) ⇒ Σ_(p=1) ^([((n−1)/2)]) ∫_p ^(p+1) (dx/(√(2x+1))) ≤ Σ_(p=1) ^([((n−1)/2)]) w_p ≤ Σ_(p=1) ^([((n−1)/2)]) ∫_(p−1) ^p (dx/(√(2x+1))) ⇒ ∫_1 ^([((n−1)/2)] +1) (dx/(√(2x+1))) ≤ Σ_(p=1) ^([((n−1)/2)]) w_p ≤ ∫_0 ^([((n−1)/2)]) (dx/(√(2x +1))) ⇒ [(√(2x+1))]_1 ^((([n−1)/2)]+1) ≤ Σ_(p=1) ^([((n−1)/2)]) w_p ≤ [(√(2x+1))]_0 ^([((n−1)/2)]) ⇒ (√(2[((n−1)/2)]+2)) −(√3)≤ Σ_(p=1) ^([((n−1)/2)]) w_p ≤(√(2[((n−1)/2)]+1))−1 ⇒ (√(2[((n−1)/2)]+2))+1−(√3)≤ Σ_(p=0) ^([((n−1)/2)]) w_p ≤ (√(2[((n−1)/2)]+1)) −2 ⇒ (√2){(√([(n/2)]+1))−1} +2−(√(2[((n−1)/2)]+1))≤ u_n ≤ (√2)(√([(n/2)])) +(√3)−1−(√(2[((n−1)/2)]+1)) ...be continued ...](Q42270.png)
| ||
Question and Answers Forum | ||
Previous in Relation and Functions Next in Relation and Functions | ||
Question Number 42190 by maxmathsup by imad last updated on 19/Aug/18 | ||
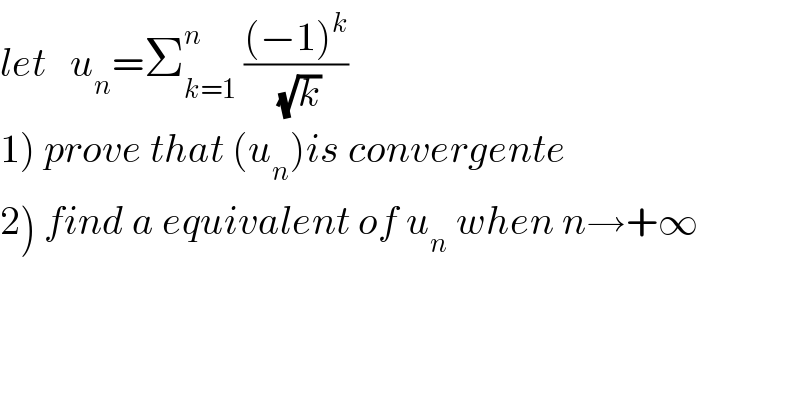 | ||
Commented by maxmathsup by imad last updated on 21/Aug/18 | ||
![1) we have lim_(n→+∞) u_n = Σ_(k=1) ^∞ (((−1)^k )/(√k)) and this serie is convergente (alternate serie) 2) we have u_n =Σ_(p=1) ^([(n/2)]) (1/(√(2p))) −Σ_(p=0) ^([((n−1)/2)]) (1/(√(2p+1))) = Σ v_p −Σw_p (v_p )is decreasing ⇒ ∫_p ^(p+1) (dx/(√(2x))) ≤ v_p ≤ ∫_(p−1) ^p (dx/(√(2x))) ⇒ Σ_(p=1) ^([(n/2)]) ∫_p ^(p+1) (dx/(√(2x))) ≤ Σ_(p=1) ^([(n/2)]) v_p ≤ Σ_(p=1) ^([(n/2)]) ∫_(p−1) ^p (dx/(√(2x))) ⇒ ∫_1 ^([(n/2)] +1) (dx/(√(2x))) ≤ Σ_(p=1) ^([(n/2)]) v_p ≤ ∫_0 ^([(n/2)]) (dx/(√(2x))) ⇒ (1/(√2))[2(√x)]_1 ^([(n/2)]+1) ≤ Σ_(p=1) ^([(n/2)]) v_p ≤(1/(√2))[2(√x)]_0 ^([(n/2)]) ⇒ (√2){(√([(n/2)]+1))−1}≤Σ v_p ≤(√2)(√([(n/2)])) also (w_p ) is decreasing ⇒ ∫_p ^(p+1) (dx/(√(2x+1))) ≤ w_p ≤ ∫_(p−1) ^p (dx/(√(2x+1))) ⇒ Σ_(p=1) ^([((n−1)/2)]) ∫_p ^(p+1) (dx/(√(2x+1))) ≤ Σ_(p=1) ^([((n−1)/2)]) w_p ≤ Σ_(p=1) ^([((n−1)/2)]) ∫_(p−1) ^p (dx/(√(2x+1))) ⇒ ∫_1 ^([((n−1)/2)] +1) (dx/(√(2x+1))) ≤ Σ_(p=1) ^([((n−1)/2)]) w_p ≤ ∫_0 ^([((n−1)/2)]) (dx/(√(2x +1))) ⇒ [(√(2x+1))]_1 ^((([n−1)/2)]+1) ≤ Σ_(p=1) ^([((n−1)/2)]) w_p ≤ [(√(2x+1))]_0 ^([((n−1)/2)]) ⇒ (√(2[((n−1)/2)]+2)) −(√3)≤ Σ_(p=1) ^([((n−1)/2)]) w_p ≤(√(2[((n−1)/2)]+1))−1 ⇒ (√(2[((n−1)/2)]+2))+1−(√3)≤ Σ_(p=0) ^([((n−1)/2)]) w_p ≤ (√(2[((n−1)/2)]+1)) −2 ⇒ (√2){(√([(n/2)]+1))−1} +2−(√(2[((n−1)/2)]+1))≤ u_n ≤ (√2)(√([(n/2)])) +(√3)−1−(√(2[((n−1)/2)]+1)) ...be continued ...](Q42270.png) | ||