let u_n =Σ_(k=1) ^n (((−1)^([k]) )/k) and H_n =Σ_(k=1) ^n (1/k) 1)calculate u_n interms of H_n 2)study the convergence of (u_n ) 3)study theconvergence of Σ u


Question and Answers Forum

All Questions Topic List
Relation and Functions Questions
Previous in All Question Next in All Question
Previous in Relation and Functions Next in Relation and Functions
Question Number 45792 by maxmathsup by imad last updated on 16/Oct/18

$l e t u_{n} = \sum_{k = 1}^{n} \frac{{(- 1)}^{[k]}}{k} a n d H_{n} = \sum_{k = 1}^{n} \frac{1}{k}$ $1) c a l c u l a t e u_{n} i n t e r m s o f H_{n}$ $2) s t u d y t h e c o n v e r g e n c e o f (u_{n})$ $3) s t u d y t h e c o n v e r g e n c e o f Σ u_{n .}$
Commented by maxmathsup by imad last updated on 17/Oct/18

$3) {l i m}_{n \to + \infty} u_{n} \neq 0 \Rightarrow Σ u_{n} d i v e r g e s . .$
Commented by maxmathsup by imad last updated on 17/Oct/18

$2) c o n v e r g e n c e o f (u_{n}) ?$ $w e h a v e u_{2 n} = \frac{1}{2} H_{n} + \frac{1}{2} H_{n - 1} - H_{2 n - 1}$ $= \frac{1}{2} (l n (n) + γ + o (\frac{1}{n})) + \frac{1}{2} (l n (n - 1) + γ + o (\frac{1}{n})) - l n (2 n - 1) - γ - o (\frac{1}{n})$ $= l n \sqrt{n (n + 1)} - l n (2 n - 1) + o (\frac{1}{n}) = l n (\frac{\sqrt{n^{2} + n}}{2 n - 1}) + o (\frac{1}{n}) \to - l n (2) (n \to + \infty)$ $u_{2 n + 1} = \frac{1}{2} H_{n} + \frac{1}{2} H_{n} - H_{2 n + 1} = H_{n} - H_{2 n + 1}$ $= l n (n) + γ - l n (2 n + 1) - γ + o (\frac{1}{n}) = l n (\frac{n}{2 n + 1}) + o (\frac{1}{n}) \to - l n (2) (n \to + \infty)$ $s o (u_{n}) c o n v e r g e s a n d {l i m}_{n \to + \infty} u_{n} = - l n (2) .$
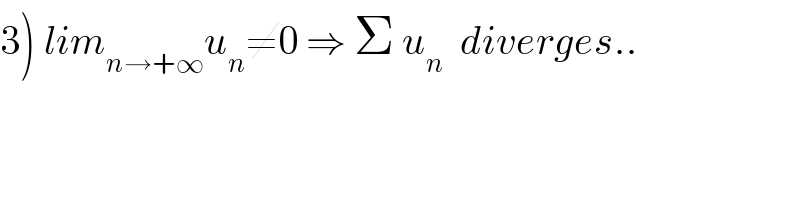
Commented by maxmathsup by imad last updated on 17/Oct/18

$w e h a v e u_{n} = \sum_{k = 1}^{n} \frac{{(- 1)}^{[k]}}{k} \Rightarrow u_{n} = \sum_{p = 1}^{[\frac{n}{2}]} \frac{1}{2 p} - \sum_{p = 0}^{[\frac{n - 1}{2}]} \frac{1}{2 p + 1} b u t$ $\sum_{p = 1}^{[\frac{n}{2}]} \frac{1}{2 p} = \frac{1}{2} H_{[\frac{n}{2}]}$ $\sum_{p = 0}^{[\frac{n - 1}{2}]} \frac{1}{2 p + 1} = 1 + \frac{1}{3} + \frac{1}{5} + . . . . + \frac{1}{2 [\frac{n - 1}{2}] + 1}$ $= 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + . . . . . + \frac{1}{2 [\frac{n - 1}{2}]} + \frac{1}{2 [\frac{n - 1}{2}] + 1} - \frac{1}{2} (1 + \frac{1}{2} + . . . . + \frac{1}{2 [\frac{n - 1}{2}]})$ $= H_{2 [\frac{n - 1}{2}] + 1} - \frac{1}{2} H_{[\frac{n - 1}{2}]} \Rightarrow$ $u_{n} = \frac{1}{2} H_{[\frac{n}{2}]} + \frac{1}{2} H_{[\frac{n - 1}{2}]} - H_{2 [\frac{n - 1}{2}] + 1}$
	Answered by arcana last updated on 17/Oct/18

	$1) c o m o u_{n} = \underset{k = 1}{\sum^{n}} \frac{{(- 1)}^{k}}{k}$ $s i n = 2 t e s p a r (p a r a a l g u n t e n t e r o p o s i t i v o)$ $u_{n} = \underset{k = 1}{\sum^{n / 2}} \frac{{(- 1)}^{2 k - 1}}{2 k - 1} + \underset{k = 1}{\sum^{n / 2}} \frac{{(- 1)}^{2 k}}{2 k}$ $= - \underset{k = 1}{\sum^{n / 2}} \frac{1}{2 k - 1} + \underset{k = 1}{\sum^{n / 2}} \frac{1}{2 k}$ $= - \underset{k = 1}{\sum^{n / 2}} \frac{1}{2 k - 1} + \frac{1}{2} H_{n / 2}$ $t o m a n d o m = 2 k - 1, l u e g o$ $= - \underset{m = 1}{\sum^{n - 1}} \frac{1}{m} + \frac{1}{2} H_{n / 2} = \frac{1}{2} H_{n / 2} - H_{n - 1}$ $s i n = 2 t - 1 e s i m p a r, t e n e m o s$ $u_{n} = \underset{k = 1}{\sum^{(n + 1) / 2}} \frac{{(- 1)}^{2 k - 1}}{2 k - 1} + \underset{k = 1}{\sum^{(n - 1) / 2}} \frac{{(- 1)}^{2 k}}{2 k}$ $= - \underset{k = 1}{\sum^{(n + 1) / 2}} \frac{1}{2 k - 1} + \underset{k = 1}{\sum^{(n - 1) / 2}} \frac{1}{2 k}$ $= - \underset{k = 1}{\sum^{(n + 1) / 2}} \frac{1}{2 k - 1} + \frac{1}{2} H_{(n - 1) / 2}$ $t o m a n d o m = 2 k - 1$ $= - \underset{m = 1}{\sum^{n}} \frac{1}{m} + \frac{1}{2} H_{(n - 1) / 2} = - H_{n} + \frac{1}{2} H_{(n - 1) / 2}$
	Commented by maxmathsup by imad last updated on 17/Oct/18

	$t h a n k y o u A r k a n a f o r t h i s w o r k . . .$
	Answered by arcana last updated on 17/Oct/18

	$3 . c o m o \frac{1}{1 + x} = \underset{k = 0}{\sum^{\infty}} {(- x)}^{k} p a r a ∣ x ∣< 1$ $i n t e g r a n d o a a m b o s l a d o s v e m o s q u e$ $\Rightarrow l n (1 + x) = \underset{k = 0}{\sum^{\infty}} \frac{{(- 1)}^{k + 1}}{k + 1} \cdot x^{k + 1}$ $c o n - 1 < x ⩽ 1 . S i x = 1, e n t o n c e s$ $l n (2) = \underset{k = 0}{\sum^{\infty}} \frac{{(- 1)}^{k + 1}}{k + 1} = Σ u_{n}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum