
Question and Answers Forum
Question Number 35632 by abdo mathsup 649 cc last updated on 21/May/18
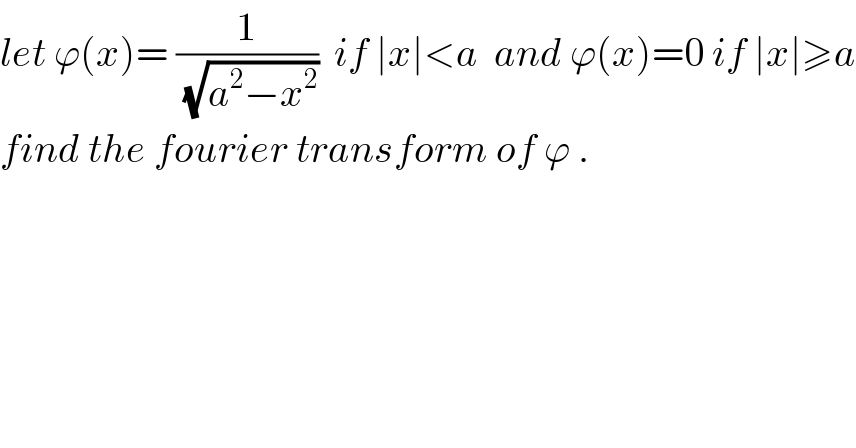
Commented by abdo mathsup 649 cc last updated on 21/May/18
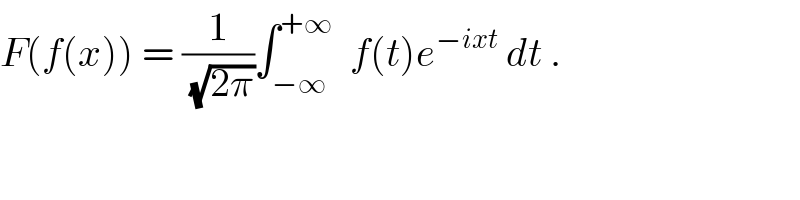
Commented by abdo mathsup 649 cc last updated on 24/May/18
![we have F(ϕ(x))= (1/(√(2π))) ∫_(−∞) ^(+∞) ϕ(t) e^(−ixt) dt and ϕ is even F(ϕ(x))o= (1/(√(2π))) ∫_(−∞) ^(+∞) ϕ(t) e^(−ixt) dt =(1/(√(2π))) ∫_(−a) ^a (e^(−ixt) /(√(a^2 −t^2 ))) dt =(√(2/π)) ∫_0 ^a ((cos(xt))/(√(a^2 −t^2 )))dt let find w(x) =∫_0 ^a ((cos(xt))/(√(a^2 −t^2 )))dt we hsve w^′ (x) = ∫_0 ^a ((−t sin(xt))/(√(a^2 −t^2 ))) and by parts w^′ (x) = [ (√(a^2 −t^2 )) sin(xt)]_0 ^a −∫_0 ^a (√(a^2 −t^2 )) x cos(xt)dt = −x ∫_0 ^a (√(a^2 −t^2 )) cos(xt)dt chsngement t =asinα give w^′ (x) = ∫_0 ^(π/2) a cos(α)cos(ax sinα) a cosα dα = a^2 ∫_0 ^(π/2) cos^2 (α) cos(ax sinα)dα =a^2 ∫_0 ^(π/2) cos(α) (cos(α) cos(ax sinα))dα =a^2 { (1/(ax)) sin(ax sin(α))cos(α)]_0 ^(π/2) − ∫_0 ^(π/2) −sin(α) sin(ax sinα) dα} = ∫_0 ^(π/2) sin(α) sin(ax sinα)dα ....be continued...](Q35812.png)
| ||
Question and Answers Forum | ||
Question Number 35632 by abdo mathsup 649 cc last updated on 21/May/18 | ||
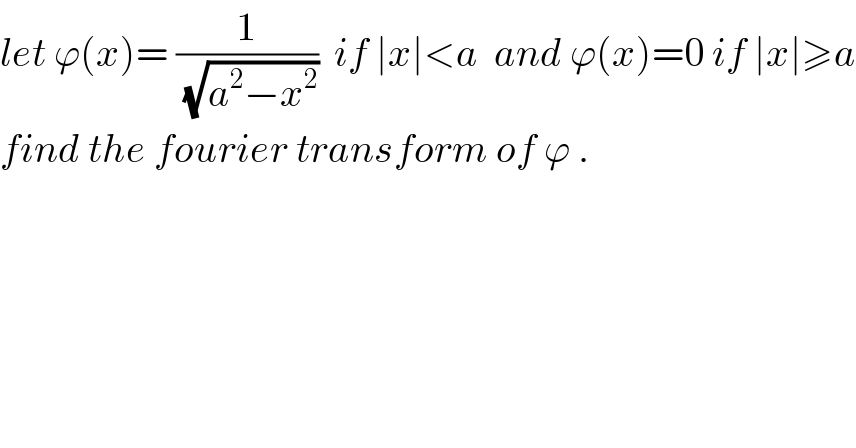 | ||
Commented by abdo mathsup 649 cc last updated on 21/May/18 | ||
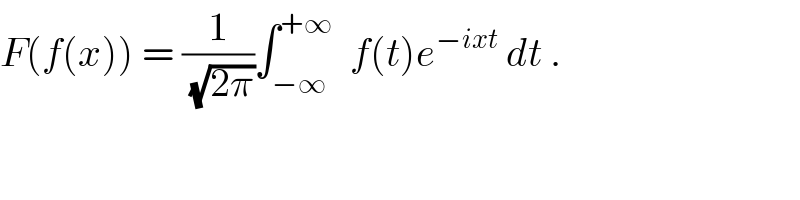 | ||
Commented by abdo mathsup 649 cc last updated on 24/May/18 | ||
![we have F(ϕ(x))= (1/(√(2π))) ∫_(−∞) ^(+∞) ϕ(t) e^(−ixt) dt and ϕ is even F(ϕ(x))o= (1/(√(2π))) ∫_(−∞) ^(+∞) ϕ(t) e^(−ixt) dt =(1/(√(2π))) ∫_(−a) ^a (e^(−ixt) /(√(a^2 −t^2 ))) dt =(√(2/π)) ∫_0 ^a ((cos(xt))/(√(a^2 −t^2 )))dt let find w(x) =∫_0 ^a ((cos(xt))/(√(a^2 −t^2 )))dt we hsve w^′ (x) = ∫_0 ^a ((−t sin(xt))/(√(a^2 −t^2 ))) and by parts w^′ (x) = [ (√(a^2 −t^2 )) sin(xt)]_0 ^a −∫_0 ^a (√(a^2 −t^2 )) x cos(xt)dt = −x ∫_0 ^a (√(a^2 −t^2 )) cos(xt)dt chsngement t =asinα give w^′ (x) = ∫_0 ^(π/2) a cos(α)cos(ax sinα) a cosα dα = a^2 ∫_0 ^(π/2) cos^2 (α) cos(ax sinα)dα =a^2 ∫_0 ^(π/2) cos(α) (cos(α) cos(ax sinα))dα =a^2 { (1/(ax)) sin(ax sin(α))cos(α)]_0 ^(π/2) − ∫_0 ^(π/2) −sin(α) sin(ax sinα) dα} = ∫_0 ^(π/2) sin(α) sin(ax sinα)dα ....be continued...](Q35812.png) | ||