
Question and Answers Forum
Question Number 174374 by Best1 last updated on 31/Jul/22
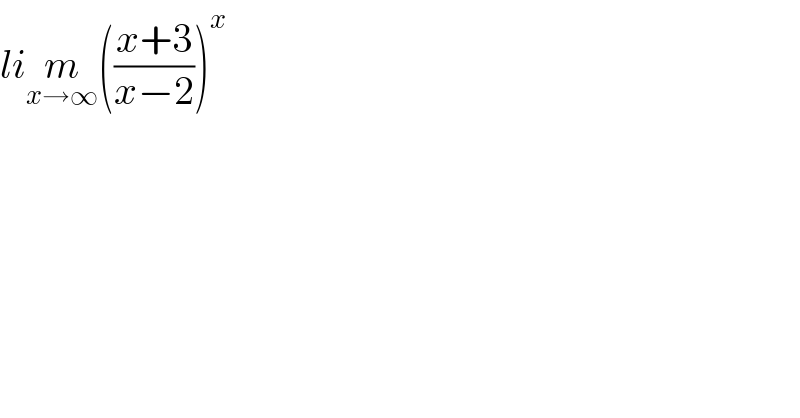
Answered by LEKOUMA last updated on 31/Jul/22
![lim_(x→∞) [f(x)]^(g(x)) lim_(x→∞) f(x)=1 et lim_(x→∞) g(x)=∞ lim_(x→∞) [f(x)]^(g(x)) =1^∞ (F.I) lim_(x→∞) [f(x)]^(g(x)) =e^(lim_(x→∞) [f(x)−1]g(x)) lim_(x→∞) (((x+3)/(x−2)))^x =1^∞ (F.I) e^(lim_(x→∞) (((x+3)/(x−2))−1)(x)) =e^(lim_(x→∞) (((x+3−1(x−2))/(x−2)))(x)) =e^(lim_(x→∞) (((x+3−x+2)/(x−2)))(x)) =e^(lim_(x→∞) ((5/(x−2)))(x)) =e^(lim_(x→∞) ((5x)/(x−2))) =e^(lim_(x→∞) ((5x)/x)) =e^(lim_(x→∞) 5) =e^5 Donc: lim_(x→∞) (((x+3)/(x−2)))^x =e^5](Q174380.png)
Commented by Best1 last updated on 31/Jul/22
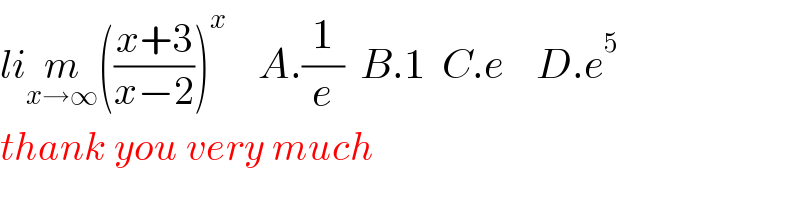
Commented by Best1 last updated on 31/Jul/22

Answered by CElcedricjunior last updated on 31/Jul/22

