Σ_(m = 1) ^∞ Σ_(n = 1) ^∞ (1/(mn(m+n))) ?


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 99005 by bobhans last updated on 18/Jun/20

$\underset{m = 1}{\sum^{\infty}} \underset{n = 1}{\sum^{\infty}} \frac{1}{mn (m + n)} ?$
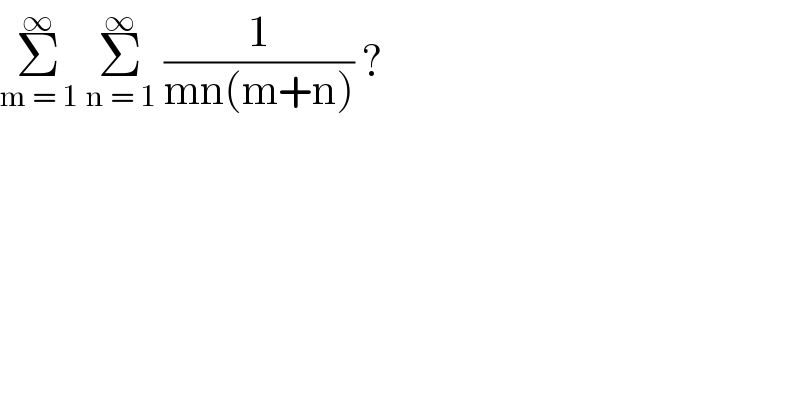
	Answered by maths mind last updated on 18/Jun/20

	$\sum_{m ⩾ 1} . \frac{1}{m^{2}} \sum_{n ⩾ 1} . \frac{(n + m) - n}{n (n + m)}$ $= \sum_{m ⩾ 1} \frac{1}{m^{2}} . \sum_{n ⩾ 1} (\frac{1}{n} - \frac{1}{n + m})$ $= \sum_{m ⩾ 1} \frac{1}{m^{2}} . H_{m}$ $= \sum_{m ⩾ 1} \frac{H_{m}}{m^{2}}$ $\int_{0}^{1} x^{n - 1} l n (1 - x) d x = - \frac{H_{n}}{n}$ $\Rightarrow \sum_{m ⩾ 1} \frac{H_{m}}{m^{2}} = - \int_{0}^{1} \sum_{m ⩾ 1} \frac{x^{m - 1}}{m} l n (1 - x)$ $= \int_{0}^{1} - \frac{1}{x} (\sum_{m ⩾ 1} \frac{x^{m}}{m}) l n (1 - x) d x$ $= \int_{0}^{1} \frac{{l n}^{2} (1 - x)}{x} d x$ $= \int_{0}^{1} \frac{{l n}^{2} (t)}{1 - t} d t, l n (t) = - r \Rightarrow$ $= \int_{0}^{\infty} \frac{t^{2} e^{- t} d t}{1 - e^{- t}} = \int_{0}^{+ \infty} \frac{t^{2} d t}{e^{t} - 1} = Γ (3) ζ (3)$ $i u s e d \int_{0}^{+ \infty} \frac{t^{a - 1}}{e^{t} - 1} = Γ (a) ζ (a) f o r R e (a) > 1$ $w e g e t Γ (3) ζ (3) = 2 ζ (3) = \sum_{m ⩾ 1} . \sum_{n ⩾ 1} \frac{1}{m n (n + m)}$
	Answered by bemath last updated on 18/Jun/20
	$∫_0 ^1 ∫_0 ^1 ∫_0 ^1 ((z dxdydz)/((1−xz)(1−yz))) = ∫_0 ^1 z {∫_0 ^1 (dx/(1−xz)) ∫_0 ^1 (dy/(1−yz)) } dz = ∫_0 ^1 z {[ ((−ln(1−xz))/z) ]_0 ^1 × [((−ln(1−yz))/z)]_0 ^1 } dz = ∫_0 ^1 ((( ln(1−z))^2 )/z) dz , set 1−z =t = ∫_0 ^1 ((( ln(t))^2 )/(1−t)) dt = ∫_0 ^1 (ln (t))^2 Σ_(n=0) ^∞ t^n = Σ_(n=0) ^∞ ∫_0 ^1 t^n (ln (t))^2 dt = 2 Σ_(n=0) ^∞ (1/((n+1)^3 )) = 2 Σ_(n=0) ^∞ (1/n^3 ) = 2 ζ(3) ■$
	$\int_{0}^{1} \int_{0}^{1} \int_{0}^{1} \frac{z dxdydz}{(1 - xz) (1 - yz)} =$ $\int_{0}^{1} z {\int_{0}^{1} \frac{dx}{1 - xz} \int_{0}^{1} \frac{dy}{1 - yz}} dz =$ $\int_{0}^{1} z {{[\frac{- \ln (1 - xz)}{z}]}_{0}^{1} \times {[\frac{- \ln (1 - yz)}{z}]}_{0}^{1}} dz$ $= \int_{0}^{1} \frac{{(\ln (1 - z))}^{2}}{z} dz, set 1 - z = t$ $= \int_{0}^{1} \frac{{(\ln (t))}^{2}}{1 - t} dt = \int_{0}^{1} {(\ln (t))}^{2} \underset{n = 0}{\sum^{\infty}} t^{n}$ $= \underset{n = 0}{\sum^{\infty}} \int_{0}^{1} t^{n} {(\ln (t))}^{2} dt$ $= 2 \underset{n = 0}{\sum^{\infty}} \frac{1}{{(n + 1)}^{3}} = 2 \underset{n = 0}{\sum^{\infty}} \frac{1}{n^{3}}$ $= 2 ζ (3) ◼$
	Commented by maths mind last updated on 18/Jun/20

	$n i c e$ $\frac{1}{(n + 1) . (m + 1) (n + m + 2)}$ $j u s t a l i t t e l j u s t i f a c t i o n$ $\int_{0}^{1} x^{n} d x . \int_{0}^{1} y^{m} d y . \int_{0}^{1} z^{n + m + 1} d z$ $= \frac{1}{n + 1} . \frac{1}{m + 1} . \frac{1}{(n + m + 2)}$ $= \int_{0}^{1} z \int_{0}^{1} {(x z)}^{n} d x . \int_{0}^{1} {(z y)}^{m} d y . d z$ $\sum_{m} . \sum_{n} \int_{0}^{1} z \int_{0}^{1} {(x z)}^{n} d x . \int_{0}^{1} {(y z)}^{m} d y . d z$ $= \int_{0}^{1} \int_{0}^{1} \int_{0}^{1} \frac{z d x d y d z}{(1 - x z) (1 - y z)} = Σ Σ \frac{1}{n m (n + m)}$
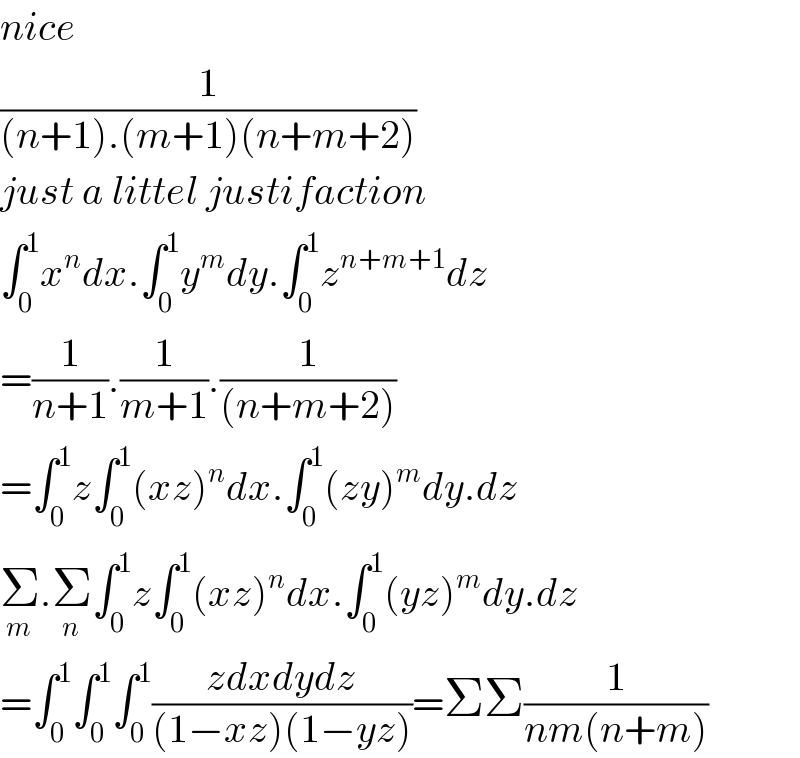
	Commented by bemath last updated on 18/Jun/20

	$great sir$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum