
Question and Answers Forum
Question Number 146735 by qaz last updated on 15/Jul/21
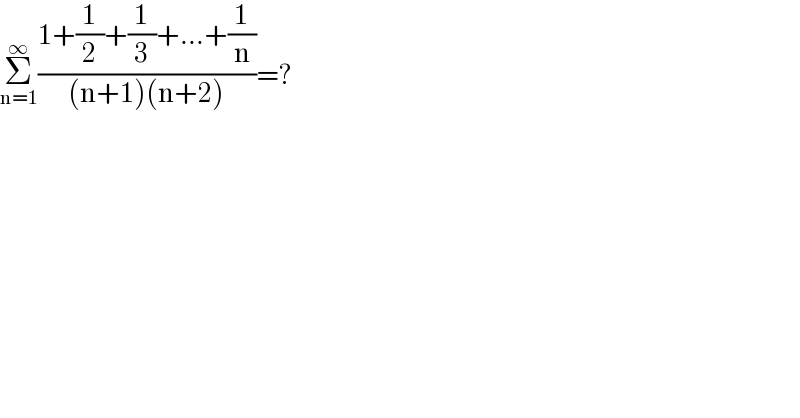
Answered by Olaf_Thorendsen last updated on 15/Jul/21
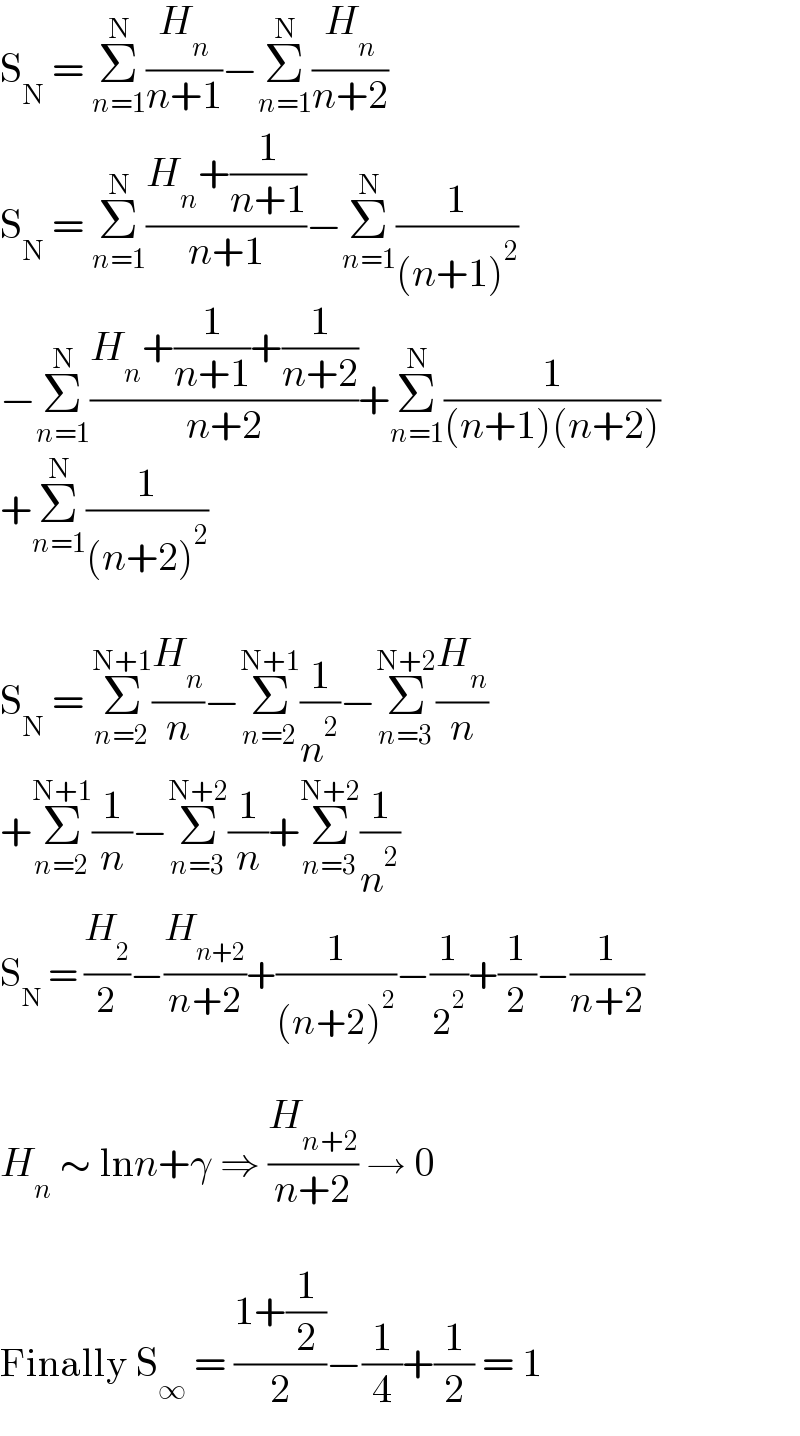
Answered by mnjuly1970 last updated on 15/Jul/21
![solution.. we know that: Σ_(n≥1) ((H_n x^( n+1) )/(n+1)) = (1/2) log^( 2) (1−x ) Σ_(n≥1) (H_n /((n+1)(n+2))) =(1/2) ∫_0 ^( 1) log^2 (x)dx = (1/2) {[xlog^( 2) (x)]_0 ^( 1) −2 ∫_0 ^( 1) log(x)dx} = −∫_0 ^( 1) log(x)dx =1....✓](Q146740.png)
Commented by qaz last updated on 15/Jul/21
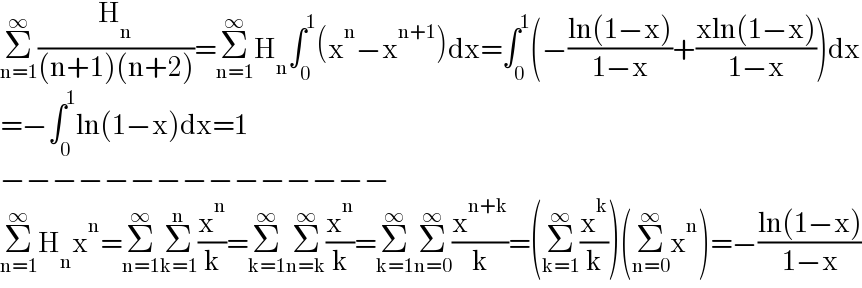
| ||
Question and Answers Forum | ||
Question Number 146735 by qaz last updated on 15/Jul/21 | ||
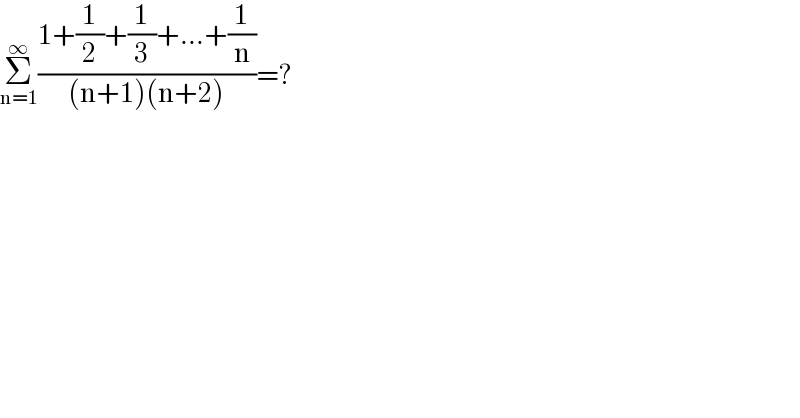 | ||
Answered by Olaf_Thorendsen last updated on 15/Jul/21 | ||
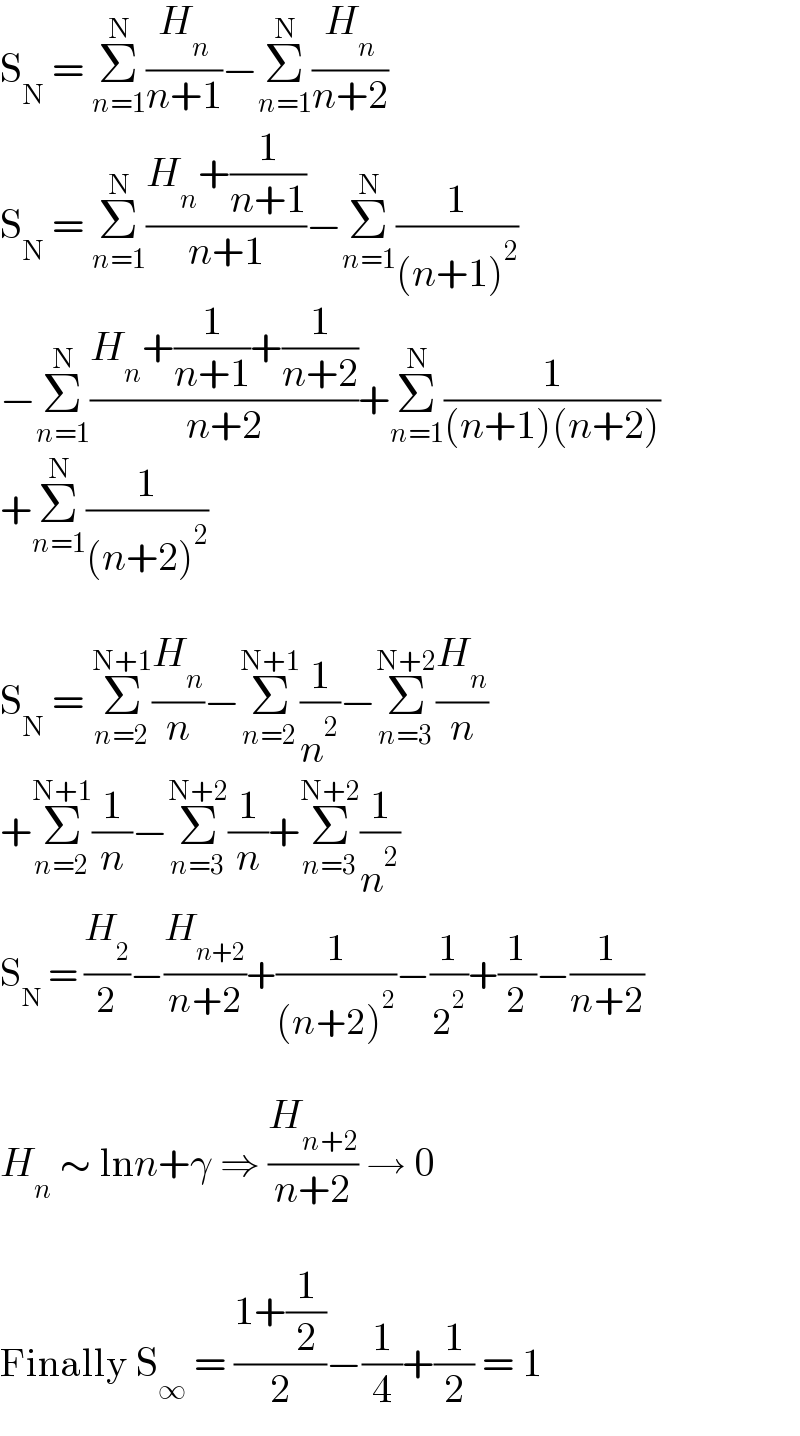 | ||
| ||
Answered by mnjuly1970 last updated on 15/Jul/21 | ||
![solution.. we know that: Σ_(n≥1) ((H_n x^( n+1) )/(n+1)) = (1/2) log^( 2) (1−x ) Σ_(n≥1) (H_n /((n+1)(n+2))) =(1/2) ∫_0 ^( 1) log^2 (x)dx = (1/2) {[xlog^( 2) (x)]_0 ^( 1) −2 ∫_0 ^( 1) log(x)dx} = −∫_0 ^( 1) log(x)dx =1....✓](Q146740.png) | ||
| ||
Commented by qaz last updated on 15/Jul/21 | ||
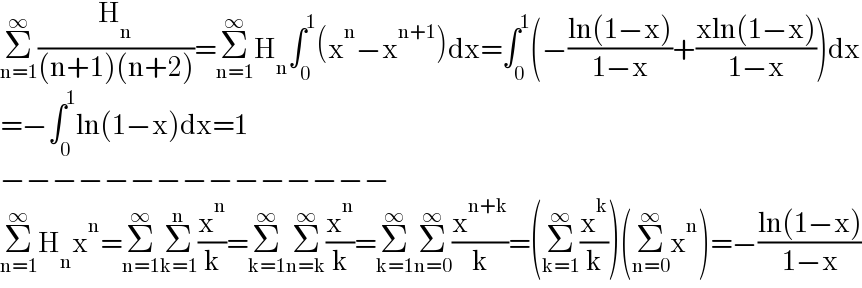 | ||