
Question and Answers Forum
Question Number 162001 by SANOGO last updated on 25/Dec/21
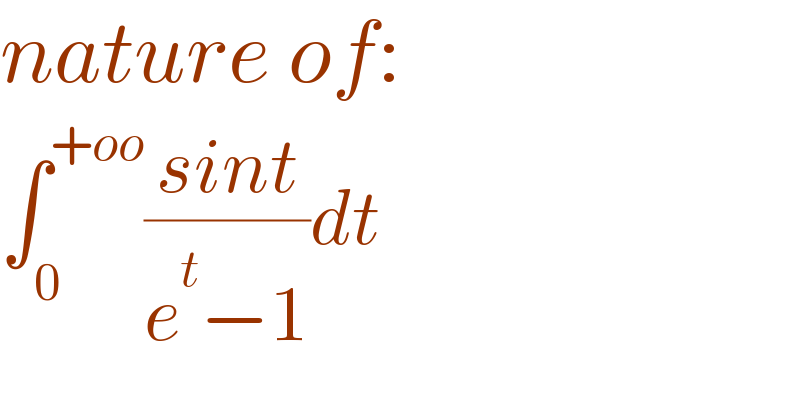
Answered by mathmax by abdo last updated on 25/Dec/21
![Ψ=∫_0 ^∞ ((sint)/(e^t −1))dt ⇒Ψ=∫_0 ^∞ ((e^(−t) sint)/(1−e^(−t) ))dt =∫_0 ^∞ e^(−t) sint Σ_(n=0) ^∞ e^(−nt) dt =Σ_(n=0) ^∞ ∫_0 ^∞ e^(−(n+1)t) sint dt but ∫_0 ^∞ e^(−(n+1)t) sint dt =Im(∫_0 ^∞ e^(−(n+1)t+it) dt) and ∫_0 ^∞ e^((−(n+1)+i)t) dt =[(1/(−(n+1)+i))e^((−(n+1)+i)t) ]_0 ^∞ =−(1/(n+1−i))(−1) =(1/(n+1−i))=((n+1+i)/((n+1)^2 +1)) ⇒ Ψ=Σ_(n=0) ^∞ (1/((n+1)^2 +1))=Σ_(n=1) ^∞ (1/(n^2 +1)) et cette serie est convergente donc Ψ est cv.](Q162005.png)
Commented by Ar Brandon last updated on 25/Dec/21
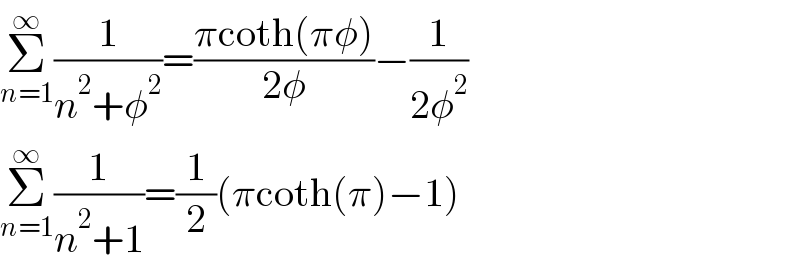
Commented by SANOGO last updated on 25/Dec/21
| ||
Question and Answers Forum | ||
Question Number 162001 by SANOGO last updated on 25/Dec/21 | ||
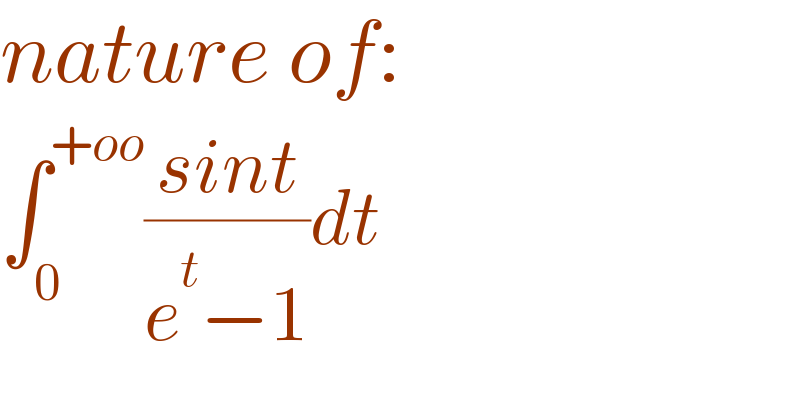 | ||
Answered by mathmax by abdo last updated on 25/Dec/21 | ||
![Ψ=∫_0 ^∞ ((sint)/(e^t −1))dt ⇒Ψ=∫_0 ^∞ ((e^(−t) sint)/(1−e^(−t) ))dt =∫_0 ^∞ e^(−t) sint Σ_(n=0) ^∞ e^(−nt) dt =Σ_(n=0) ^∞ ∫_0 ^∞ e^(−(n+1)t) sint dt but ∫_0 ^∞ e^(−(n+1)t) sint dt =Im(∫_0 ^∞ e^(−(n+1)t+it) dt) and ∫_0 ^∞ e^((−(n+1)+i)t) dt =[(1/(−(n+1)+i))e^((−(n+1)+i)t) ]_0 ^∞ =−(1/(n+1−i))(−1) =(1/(n+1−i))=((n+1+i)/((n+1)^2 +1)) ⇒ Ψ=Σ_(n=0) ^∞ (1/((n+1)^2 +1))=Σ_(n=1) ^∞ (1/(n^2 +1)) et cette serie est convergente donc Ψ est cv.](Q162005.png) | ||
| ||
Commented by Ar Brandon last updated on 25/Dec/21 | ||
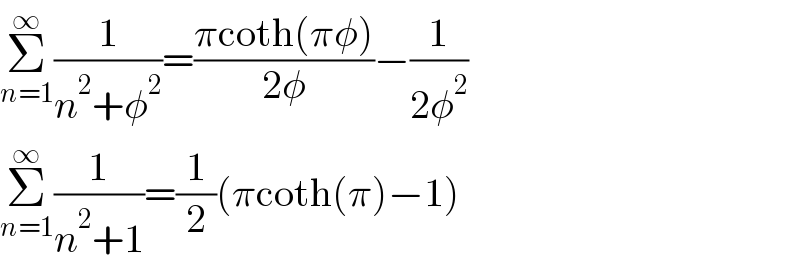 | ||
Commented by SANOGO last updated on 25/Dec/21 | ||
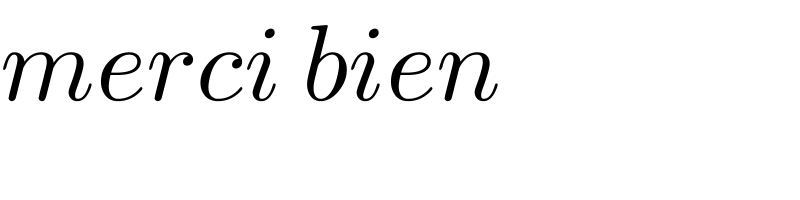 | ||