new attempt to solve qu. 37630 ∫(dx/((√x)+(√(x+1))+(√(x+2))))= [t=x+1 → dx=dt] =∫(dt/((√(t−1))+(√t)+(√(t+1))))= [((to omit the roots)),(((√a)+(√b)+(√c) must be multiplied with)),(((−(√a)−(√b)+(√c))(−(√a)+(√b)−(√c))((√a)−(√b)−(√c)))),(((1/((√a)+(√b)+(√c)))=((a^(3/2) +b^(3/2) +c^(3/2) +2(√(abc))−((a+b)(√c)+(a+c)(√b)+(b+c)(√a)))/(a^2 +b^2 +c^2 −2(ab+ac+bc))))) ] =∫((t(√(t−1))+t(√t)+t(√(t+1))+2(√(t−1))−2(√(t+1))−2(√((t−1)t(t+1))))/(3t^2 −4))dt= =∫((t(√(t−1)))/(3t^2 −4))dt+∫((t(√t))/(3t^2 −4))dt+∫((t(√(t+1)))/(3t^2 −4))dt+2∫((√(t−1))/(3t^2 −4))dt−2∫((√(t+1))/(3t^2 −4))−2∫((√((t−1)t(t+1)))/(3t^2 −4))dt I think I can solve them all except the last one so please somebody try ∫((√((t−1)t(t+1)))/(3t^2 −4))dt=? I will do the others tomorrow


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 38451 by MJS last updated on 25/Jun/18

$new attempt to solve qu . 37630$ $\int \frac{d x}{\sqrt{x} + \sqrt{x + 1} + \sqrt{x + 2}} =$ $[t = x + 1 \to d x = d t]$ $= \int \frac{d t}{\sqrt{t - 1} + \sqrt{t} + \sqrt{t + 1}} =$ $[\begin{matrix} to omit the roots \\ \sqrt{a} + \sqrt{b} + \sqrt{c} must be multiplied with \\ (- \sqrt{a} - \sqrt{b} + \sqrt{c}) (- \sqrt{a} + \sqrt{b} - \sqrt{c}) (\sqrt{a} - \sqrt{b} - \sqrt{c}) \\ \frac{1}{\sqrt{a} + \sqrt{b} + \sqrt{c}} = \frac{a^{3 / 2} + b^{3 / 2} + c^{3 / 2} + 2 \sqrt{a b c} - ((a + b) \sqrt{c} + (a + c) \sqrt{b} + (b + c) \sqrt{a})}{a^{2} + b^{2} + c^{2} - 2 (a b + a c + b c)} \end{matrix}]$ $= \int \frac{t \sqrt{t - 1} + t \sqrt{t} + t \sqrt{t + 1} + 2 \sqrt{t - 1} - 2 \sqrt{t + 1} - 2 \sqrt{(t - 1) t (t + 1)}}{3 t^{2} - 4} d t =$ $= \int \frac{t \sqrt{t - 1}}{3 t^{2} - 4} d t + \int \frac{t \sqrt{t}}{3 t^{2} - 4} d t + \int \frac{t \sqrt{t + 1}}{3 t^{2} - 4} d t + 2 \int \frac{\sqrt{t - 1}}{3 t^{2} - 4} d t - 2 \int \frac{\sqrt{t + 1}}{3 t^{2} - 4} - 2 \int \frac{\sqrt{(t - 1) t (t + 1)}}{3 t^{2} - 4} d t$ $I think I can solve them all except the last one$ $so please somebody try$ $\int \frac{\sqrt{(t - 1) t (t + 1)}}{3 t^{2} - 4} d t = ?$ $I will do the others tomorrow$
Commented by math khazana by abdo last updated on 26/Jun/18

$c h a n g e m e n t t = c h (x) g i v e$ $\int \frac{\sqrt{(t - 1) t (t + 1)}}{3 t^{2} - 4} d t = \int \frac{\sqrt{{s h}^{2} x c h x}}{3 {c h}^{2} (x) - 4} s h (x) d x$ $= \int \frac{{s h}^{2} x \sqrt{c h x}}{3 {c h}^{2} (x) - 4} d x$ $=_{\sqrt{c h x} = u} \int \frac{(u^{4} - 1) u}{3 u^{4} - 4} (c h x = u^{2} \Rightarrow x = a r g c h (u^{2})$ $\Rightarrow d x = \frac{2 u d u}{\sqrt{u^{4} - 1}} \Rightarrow$ $I = \int \frac{(u^{4} - 1)}{3 u^{4} - 4} \frac{2 u d u}{\sqrt{u^{4} - 1}}$ $= 2 \int \frac{u \sqrt{u^{4} - 1}}{3 u^{4} - 4} d u = 2 \int \frac{u \sqrt{u^{4} - 1}}{4 (u^{4} - 1) - u^{4}} d u$ $=_{\sqrt{u^{4} - 1} = x} 2 \int \frac{{(1 + x^{2})}^{\frac{1}{4}} x}{4 x^{2} - (1 + x^{2})} \frac{x}{2} {(1 + x^{2})}^{- \frac{3}{4}} (u^{4} = 1 + x^{2} \Rightarrow$ $u = {(1 + x^{2})}^{\frac{1}{4}} \Rightarrow d u = \frac{x}{2} {(1 + x^{2})}^{- \frac{3}{4}}$ $I = \int \frac{x^{2}}{\sqrt{1 + x^{2}} (3 x^{2} - 1)} d x = . . .$
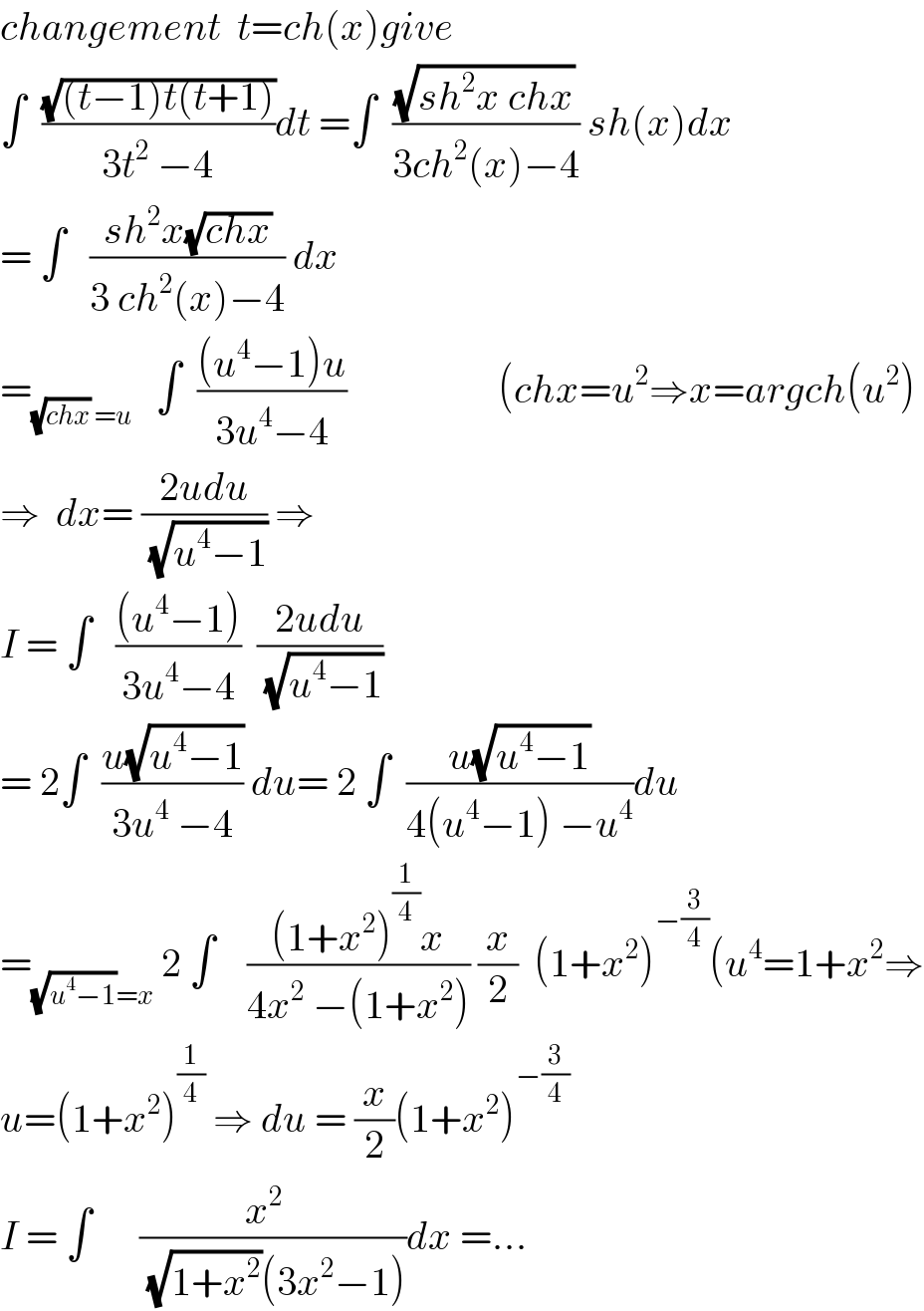
	Answered by MJS last updated on 27/Jun/18

	$\int \frac{t \sqrt{t - 1}}{3 t^{2} - 4} d t =$ $[u = \sqrt{t - 1} \to d t = 2 \sqrt{t - 1} d u]$ $= 2 \int \frac{u^{4} + u^{2}}{3 u^{4} + 6 u^{2} - 1} d u = \frac{2}{3} \int (1 - \frac{3 u^{2} - 1}{3 u^{4} + 6 u^{2} - 1}) d u =$ $= \frac{2}{3} \int d u + \frac{2}{3} \int \frac{d u}{3 u^{4} + 6 u^{2} - 1} - 2 \int \frac{u^{2}}{3 u^{4} + 6 u^{2} - 1} d u =$ $\frac{2}{3} \int d u = \frac{2}{3} u = \frac{2}{3} \sqrt{t - 1}$ $\frac{2}{3} \int \frac{d u}{3 u^{4} + 6 u^{2} - 1} = \frac{2}{9} \int \frac{d u}{u^{4} + 2 u^{2} - \frac{1}{3}} =$ $= \frac{2}{9} \int \frac{d u}{(u^{2} + \frac{3 - 2 \sqrt{3}}{3}) (u^{2} + \frac{3 + 2 \sqrt{3}}{3})} =$ $= \frac{2}{9} \int \frac{A}{u^{2} + \frac{3 - 2 \sqrt{3}}{3}} d u + \frac{2}{9} \int \frac{B}{u^{2} + \frac{3 + 2 \sqrt{3}}{3}} d u =$ $= \frac{\sqrt{3}}{18} \int \frac{d u}{u^{2} + \frac{3 - 2 \sqrt{3}}{3}} - \frac{\sqrt{3}}{18} \int \frac{d u}{u^{2} + \frac{3 + 2 \sqrt{3}}{3}} =$ $[\int \frac{d v}{v^{2} - p^{2}} = \frac{1}{2 p} \ln \frac{v - p}{v + p}; \int \frac{d v}{v^{2} + q^{2}} = \frac{1}{q} \arctan \frac{v}{q}]$ $= \frac{\sqrt{3}}{36} \sqrt{3 + 2 \sqrt{3}} \ln ∣ \frac{u - \frac{\sqrt{3}}{3} \sqrt{- 3 + 2 \sqrt{3}}}{u + \frac{\sqrt{3}}{3} \sqrt{- 3 + 2 \sqrt{3}}} ∣ - \frac{\sqrt{3}}{18} \sqrt{- 3 + 2 \sqrt{3}} \arctan \sqrt{- 3 + 2 \sqrt{3}} u =$ $= \frac{\sqrt{3}}{36} (\sqrt{3 + 2 \sqrt{3}} \ln ∣ \frac{\sqrt{t - 1} - \frac{\sqrt{3}}{3} \sqrt{- 3 + 2 \sqrt{3}}}{\sqrt{t - 1} + \frac{\sqrt{3}}{3} \sqrt{- 3 + 2 \sqrt{3}}} ∣ - 2 \sqrt{- 3 + 2 \sqrt{3}} \arctan \sqrt{(- 3 + 2 \sqrt{3}) (t - 1)})$ $- 2 \int \frac{u^{2}}{3 u^{4} + 6 u^{2} - 1} d u = - \frac{2}{3} \int \frac{u^{2}}{u^{4} + 2 u^{2} - \frac{1}{3}} d u =$ $= - \frac{2}{3} \int \frac{u^{2}}{(u^{2} + \frac{3 - 2 \sqrt{3}}{3}) (u^{2} + \frac{3 + 2 \sqrt{3}}{3})} d u =$ $= - \frac{2}{3} \int \frac{C}{u^{2} + \frac{3 - 2 \sqrt{3}}{3}} d u - \frac{2}{3} \int \frac{D}{u^{2} + \frac{3 + 2 \sqrt{3}}{3}} d u =$ $= - \frac{2 - \sqrt{3}}{6} \int \frac{d u}{u^{2} + \frac{3 - 2 \sqrt{3}}{3}} - \frac{2 + \sqrt{3}}{6} \int \frac{d u}{u^{2} + \frac{3 + 2 \sqrt{3}}{3}} =$ $= - \frac{1}{12} (\sqrt{- 3 + 2 \sqrt{3}} \ln ∣ \frac{u - \frac{\sqrt{3}}{3} \sqrt{- 3 + 2 \sqrt{3}}}{u + \frac{\sqrt{3}}{3} \sqrt{- 3 + 2 \sqrt{3}}} ∣ + 2 \sqrt{3 + 2 \sqrt{3}} \arctan \sqrt{- 3 + 2 \sqrt{3}} u) =$ $= - \frac{1}{12} (\sqrt{- 3 + 2 \sqrt{3}} \ln ∣ \frac{\sqrt{t - 1} - \frac{\sqrt{3}}{3} \sqrt{- 3 + 2 \sqrt{3}}}{\sqrt{t - 1} + \frac{\sqrt{3}}{3} \sqrt{- 3 + 2 \sqrt{3}}} ∣ + 2 \sqrt{3 + 2 \sqrt{3}} \arctan \sqrt{(- 3 + 2 \sqrt{3}) (t - 1)})$ $= \frac{2}{3} \sqrt{t - 1} + \frac{\sqrt{3}}{18} \sqrt{- 3 + 2 \sqrt{3}} \ln ∣ \frac{\sqrt{t - 1} - \frac{\sqrt{3}}{3} \sqrt{- 3 + 2 \sqrt{3}}}{\sqrt{t - 1} + \frac{\sqrt{3}}{3} \sqrt{- 3 + 2 \sqrt{3}}} ∣ + \frac{\sqrt{3}}{9} \sqrt{3 + 2 \sqrt{3}} \arctan \sqrt{(- 3 + 2 \sqrt{3}) (t - 1)}$
	Commented by MJS last updated on 27/Jun/18

	$\int \frac{t \sqrt{t + 1}}{3 t^{2} - 4} d t =$ $[same procedure as above]$ $= \frac{2}{3} \sqrt{t + 1} + \frac{\sqrt{3}}{18} \sqrt{3 + 2 \sqrt{3}} \ln ∣ \frac{\sqrt{t + 1} - \frac{\sqrt{3}}{3} \sqrt{3 + 2 \sqrt{3}}}{\sqrt{t + 1} + \frac{\sqrt{3}}{3} \sqrt{3 + 2 \sqrt{3}}} ∣ - \frac{\sqrt{3}}{9} \sqrt{- 3 + 2 \sqrt{3}} \arctan \sqrt{(3 + 2 \sqrt{3}) (t + 1)}$
	Commented by MJS last updated on 27/Jun/18

	$\int \frac{t \sqrt{t}}{3 t^{2} - 4} d t =$ $[ditto]$ $= \frac{2}{3} \sqrt{t} + \frac{\sqrt{6 \sqrt{3}}}{18} \ln ∣ \frac{\sqrt{t} - \frac{\sqrt{6 \sqrt{3}}}{3}}{\sqrt{t} + \frac{\sqrt{6 \sqrt{3}}}{3}} ∣ - \frac{\sqrt{6 \sqrt{3}}}{9} \arctan \frac{\sqrt{2 \sqrt{3} t}}{2}$
	Commented by MJS last updated on 27/Jun/18

	$2 \int \frac{\sqrt{t - 1}}{3 t^{2} - 4} d t =$ $= \frac{1}{6} \sqrt{- 3 + 2 \sqrt{3}} \ln ∣ \frac{\sqrt{t - 1} - \frac{\sqrt{3}}{3} \sqrt{- 3 + 2 \sqrt{3}}}{\sqrt{t - 1} + \frac{\sqrt{3}}{3} \sqrt{- 3 + 2 \sqrt{3}}} ∣ - \frac{1}{3} \sqrt{3 + 2 \sqrt{3}} \arctan \sqrt{(- 3 + 2 \sqrt{3}) (t - 1)}$ $- 2 \int \frac{\sqrt{t + 1}}{3 t^{2} - 4} d t =$ $= - \frac{1}{6} \sqrt{3 + 2 \sqrt{3}} \ln ∣ \frac{\sqrt{t + 1} - \frac{\sqrt{3}}{3} \sqrt{3 + 2 \sqrt{3}}}{\sqrt{t + 1} + \frac{\sqrt{3}}{3} \sqrt{3 + 2 \sqrt{3}}} ∣ - \frac{1}{3} \sqrt{- 3 + 2 \sqrt{3}} \arctan \sqrt{(3 + 2 \sqrt{3}) (t + 1)}$
	Commented by MJS last updated on 27/Jun/18

	$\int \frac{d t}{\sqrt{t - 1} + \sqrt{t} + \sqrt{t + 1}} =$ $= \frac{2}{3} (\sqrt{t - 1} + \sqrt{t} + \sqrt{t + 1}) +$ $+ \frac{\sqrt{6 \sqrt{3}}}{18} (\ln ∣ \frac{\sqrt{t - 1} - \frac{\sqrt{3}}{3} \sqrt{- 3 + 2 \sqrt{3}}}{\sqrt{t - 1} + \frac{\sqrt{3}}{3} \sqrt{- 3 + 2 \sqrt{3}}} ∣ + \ln ∣ \frac{\sqrt{t} - \frac{\sqrt{6 \sqrt{3}}}{3}}{\sqrt{t} + \frac{\sqrt{6 \sqrt{3}}}{3}} ∣ - \ln ∣ \frac{\sqrt{t + 1} - \frac{\sqrt{3}}{3} \sqrt{- 3 + 2 \sqrt{3}}}{\sqrt{t + 1} + \frac{\sqrt{3}}{3} \sqrt{- 3 + 2 \sqrt{3}}} ∣) +$ $- \frac{\sqrt{6 \sqrt{3}}}{9} (\arctan \sqrt{(- 3 + 2 \sqrt{3}) (t - 1)} + \arctan \frac{\sqrt{2 \sqrt{3} t}}{2} + \arctan \sqrt{(3 + 2 \sqrt{3}) (t + 1)}) -$ $- 2 \int \frac{\sqrt{(t - 1) t (t + 1)}}{3 t^{2} - 4} d t + C$ $under construction$
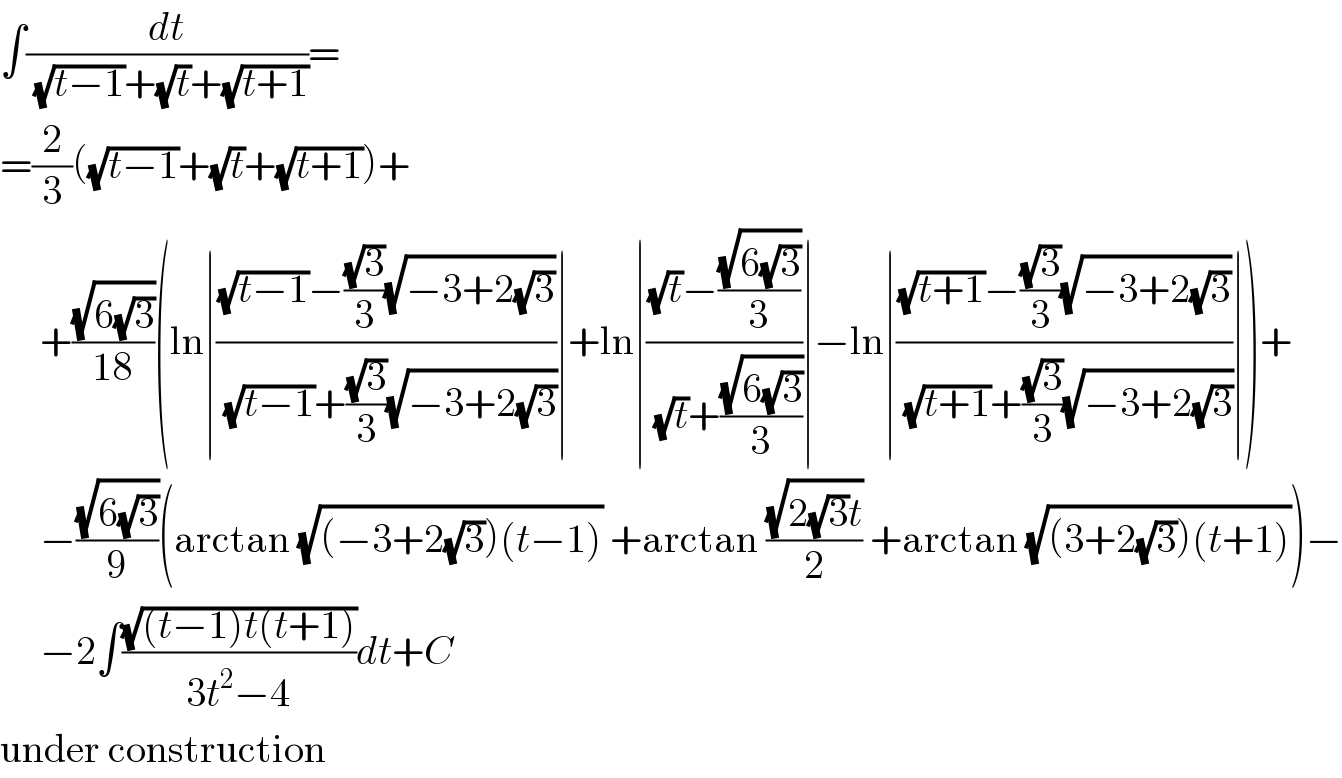
	Commented by math khazana by abdo last updated on 27/Jun/18

	$s i r M j s y o u a r e r e a l l y t i r e d w i t h t h i s i t e g r a l$ $t h a n k y o u f o r t h i s h a r d w o r k y o u a r e r e a l l y$ $p a t i e n t . . .$
	Commented by MJS last updated on 27/Jun/18

	$this integral is my personal nemesis LOL$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum