
Question and Answers Forum
Question Number 137874 by mnjuly1970 last updated on 07/Apr/21
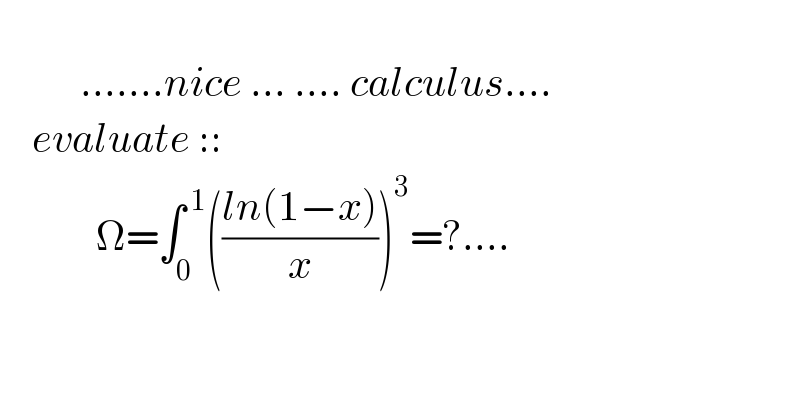
Answered by EnterUsername last updated on 07/Apr/21
![Ω=∫_0 ^1 (((ln(1−x))/x))^3 dx =∫_0 ^1 ((ln^3 x)/((1−x)^3 ))dx=[((ln^3 x)/(2(1−x)^2 ))−(3/2)∫((ln^2 x)/(x(1−x)^2 ))dx]_0 ^1 =[((ln^3 x)/(2(1−x)^2 ))−(3/2)∫((1/x)+(1/(1−x))+(1/((1−x)^2 )))ln^2 xdx]_0 ^1 =[((ln^3 x)/(2(1−x)^2 ))−((ln^3 x)/2)−(3/2)∫((ln^2 x)/(1−x))dx−(3/2)∫((ln^2 x)/((1−x)^2 ))dx]_0 ^1 =−(3/2)(∫_0 ^1 ((ln^2 x)/(1−x))dx+∫_0 ^1 ((ln^2 x)/((1−x)^2 ))dx)=−(3/2)(−ψ′′(1)+2ζ(2)) =−(3/2)(2ζ(3)+2ζ(2))=−3(ζ(3)+ζ(2))](Q137883.png)
Commented by EnterUsername last updated on 07/Apr/21
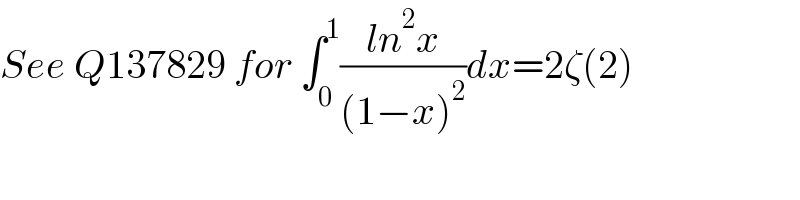
Commented by mnjuly1970 last updated on 07/Apr/21
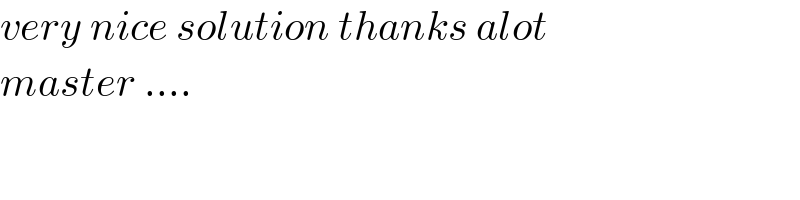
| ||
Question and Answers Forum | ||
Question Number 137874 by mnjuly1970 last updated on 07/Apr/21 | ||
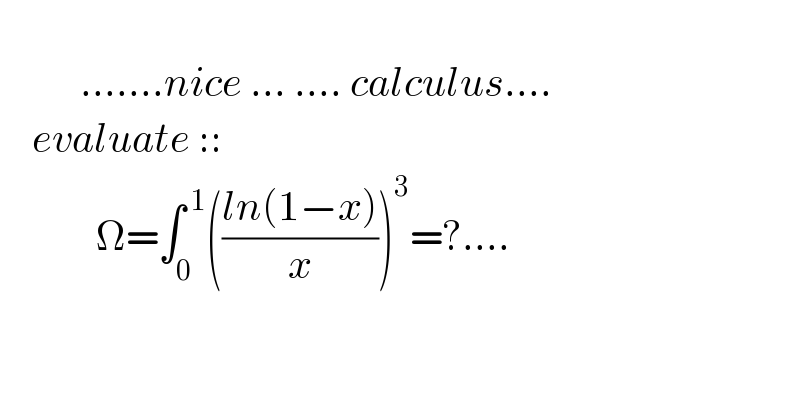 | ||
Answered by EnterUsername last updated on 07/Apr/21 | ||
![Ω=∫_0 ^1 (((ln(1−x))/x))^3 dx =∫_0 ^1 ((ln^3 x)/((1−x)^3 ))dx=[((ln^3 x)/(2(1−x)^2 ))−(3/2)∫((ln^2 x)/(x(1−x)^2 ))dx]_0 ^1 =[((ln^3 x)/(2(1−x)^2 ))−(3/2)∫((1/x)+(1/(1−x))+(1/((1−x)^2 )))ln^2 xdx]_0 ^1 =[((ln^3 x)/(2(1−x)^2 ))−((ln^3 x)/2)−(3/2)∫((ln^2 x)/(1−x))dx−(3/2)∫((ln^2 x)/((1−x)^2 ))dx]_0 ^1 =−(3/2)(∫_0 ^1 ((ln^2 x)/(1−x))dx+∫_0 ^1 ((ln^2 x)/((1−x)^2 ))dx)=−(3/2)(−ψ′′(1)+2ζ(2)) =−(3/2)(2ζ(3)+2ζ(2))=−3(ζ(3)+ζ(2))](Q137883.png) | ||
| ||
Commented by EnterUsername last updated on 07/Apr/21 | ||
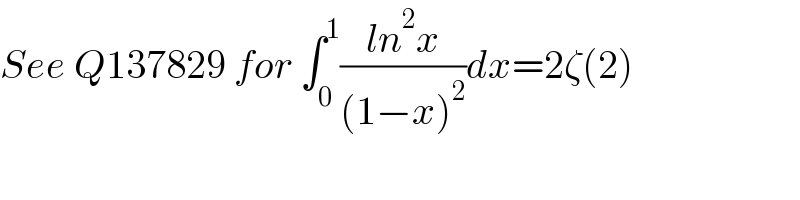 | ||
Commented by mnjuly1970 last updated on 07/Apr/21 | ||
 | ||