Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 141082 by mnjuly1970 last updated on 15/May/21

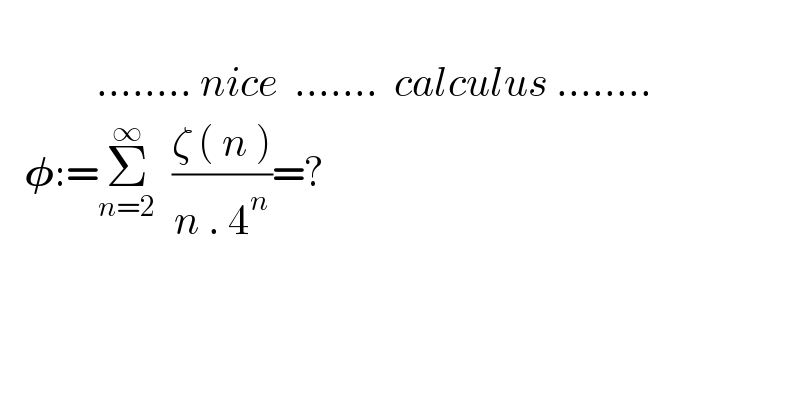
........ nice ....... calculus ........ 𝛗:=Σ_(n=2) ^∞ ((ζ ( n ))/(n . 4^n ))=?

........nice.......calculus........ϕ:=∑∞n=2ζ(n)n.4n=?

Answered by mindispower last updated on 15/May/21

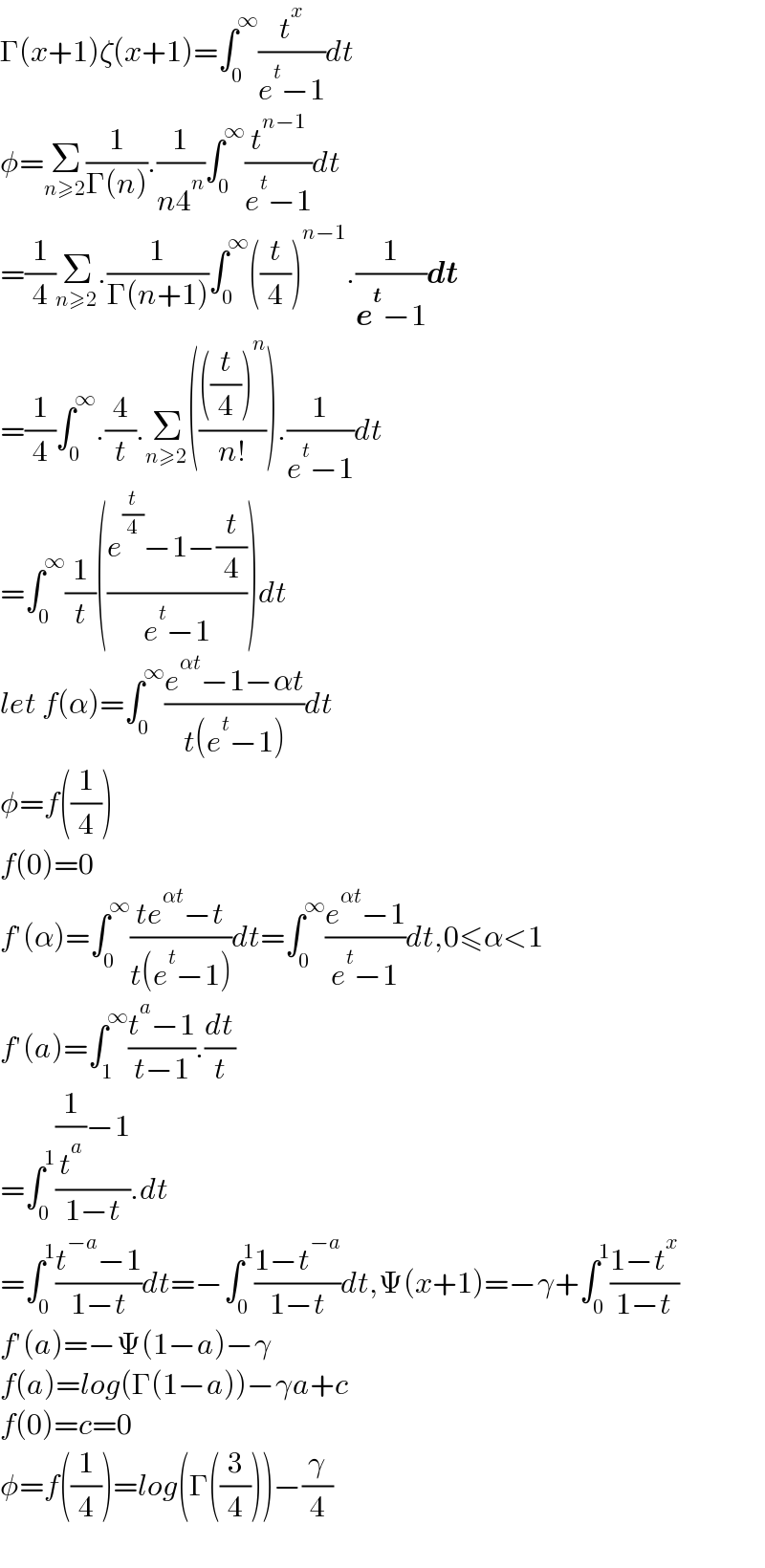
Γ(x+1)ζ(x+1)=∫_0 ^∞ (t^x /(e^t −1))dt φ=Σ_(n≥2) (1/(Γ(n))).(1/(n4^n ))∫_0 ^∞ (t^(n−1) /(e^t −1))dt =(1/4)Σ_(n≥2) .(1/(Γ(n+1)))∫_0 ^∞ ((t/4))^(n−1) .(1/(e^t −1))dt =(1/4)∫_0 ^∞ .(4/t).Σ_(n≥2) (((((t/4))^n )/(n!))).(1/(e^t −1))dt =∫_0 ^∞ (1/t)(((e^(t/4) −1−(t/4))/(e^t −1)))dt let f(α)=∫_0 ^∞ ((e^(αt) −1−αt)/(t(e^t −1)))dt φ=f((1/4)) f(0)=0 f′(α)=∫_0 ^∞ ((te^(αt) −t)/(t(e^t −1)))dt=∫_0 ^∞ ((e^(αt) −1)/(e^t −1))dt,0≤α<1 f′(a)=∫_1 ^∞ ((t^a −1)/(t−1)).(dt/t) =∫_0 ^1 (((1/t^a )−1)/(1−t)).dt =∫_0 ^1 ((t^(−a) −1)/(1−t))dt=−∫_0 ^1 ((1−t^(−a) )/(1−t))dt,Ψ(x+1)=−γ+∫_0 ^1 ((1−t^x )/(1−t)) f′(a)=−Ψ(1−a)−γ f(a)=log(Γ(1−a))−γa+c f(0)=c=0 φ=f((1/4))=log(Γ((3/4)))−(γ/4)

Γ(x+1)ζ(x+1)=∫0∞txet−1dtϕ=∑n⩾21Γ(n).1n4n∫0∞tn−1et−1dt=14∑n⩾2.1Γ(n+1)∫0∞(t4)n−1.1et−1dt=14∫0∞.4t.∑n⩾2((t4)nn!).1et−1dt=∫0∞1t(et4−1−t4et−1)dtletf(α)=∫0∞eαt−1−αtt(et−1)dtϕ=f(14)f(0)=0f′(α)=∫0∞teαt−tt(et−1)dt=∫0∞eαt−1et−1dt,0⩽α<1f′(a)=∫1∞ta−1t−1.dtt=∫011ta−11−t.dt=∫01t−a−11−tdt=−∫011−t−a1−tdt,Ψ(x+1)=−γ+∫011−tx1−tf′(a)=−Ψ(1−a)−γf(a)=log(Γ(1−a))−γa+cf(0)=c=0ϕ=f(14)=log(Γ(34))−γ4

Commented by mnjuly1970 last updated on 15/May/21

bravo bravo sir power...

bravobravosirpower...

Commented by mindispower last updated on 15/May/21

withe pleasur Sir

withepleasurSir

Answered by mnjuly1970 last updated on 15/May/21

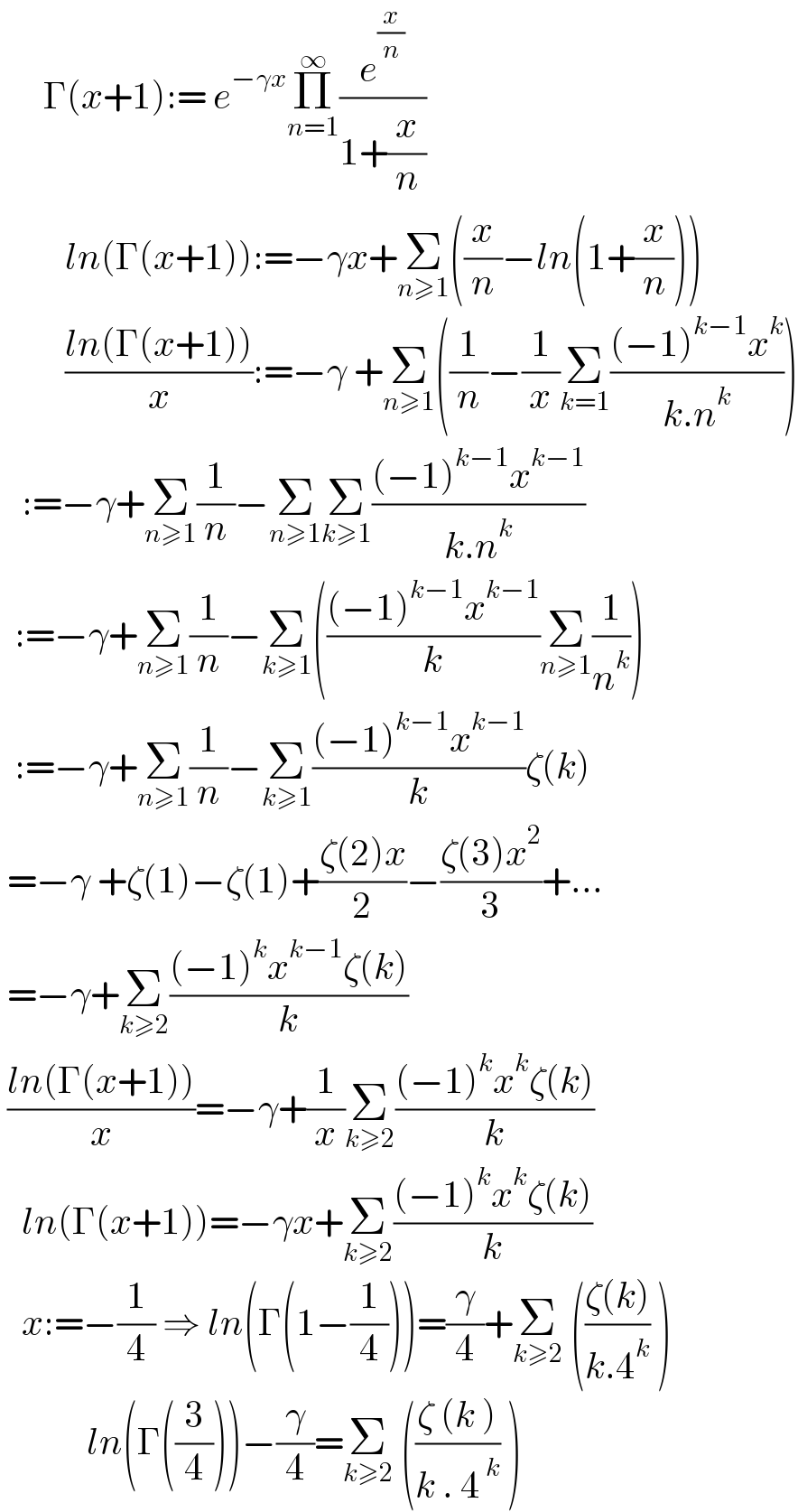
Γ(x+1):= e^(−γx) Π_(n=1) ^∞ (e^(x/n) /(1+(x/n))) ln(Γ(x+1)):=−γx+Σ_(n≥1) ((x/n)−ln(1+(x/n))) ((ln(Γ(x+1)))/x):=−γ +Σ_(n≥1) ((1/n)−(1/x)Σ_(k=1) (((−1)^(k−1) x^k )/(k.n^k ))) :=−γ+Σ_(n≥1) (1/n)−Σ_(n≥1) Σ_(k≥1) (((−1)^(k−1) x^(k−1) )/(k.n^k )) :=−γ+Σ_(n≥1) (1/n)−Σ_(k≥1) ((((−1)^(k−1) x^(k−1) )/k)Σ_(n≥1) (1/n^k )) :=−γ+Σ_(n≥1) (1/n)−Σ_(k≥1) (((−1)^(k−1) x^(k−1) )/k)ζ(k) =−γ +ζ(1)−ζ(1)+((ζ(2)x)/2)−((ζ(3)x^2 )/3)+... =−γ+Σ_(k≥2) (((−1)^k x^(k−1) ζ(k))/k) ((ln(Γ(x+1)))/x)=−γ+(1/x)Σ_(k≥2) (((−1)^k x^k ζ(k))/k) ln(Γ(x+1))=−γx+Σ_(k≥2) (((−1)^k x^k ζ(k))/k) x:=−(1/4) ⇒ ln(Γ(1−(1/4)))=(γ/4)+Σ_(k≥2) (((ζ(k))/(k.4^k )) ) ln(Γ((3/4)))−(γ/4)=Σ_(k≥2) (((ζ (k ))/(k . 4^( k) )) )

Γ(x+1):=e−γx∏∞n=1exn1+xnln(Γ(x+1)):=−γx+∑n⩾1(xn−ln(1+xn))ln(Γ(x+1))x:=−γ+∑n⩾1(1n−1x∑k=1(−1)k−1xkk.nk):=−γ+∑n⩾11n−∑n⩾1∑k⩾1(−1)k−1xk−1k.nk:=−γ+∑n⩾11n−∑k⩾1((−1)k−1xk−1k∑n⩾11nk):=−γ+∑n⩾11n−∑k⩾1(−1)k−1xk−1kζ(k)=−γ+ζ(1)−ζ(1)+ζ(2)x2−ζ(3)x23+...=−γ+∑k⩾2(−1)kxk−1ζ(k)kln(Γ(x+1))x=−γ+1x∑k⩾2(−1)kxkζ(k)kln(Γ(x+1))=−γx+∑k⩾2(−1)kxkζ(k)kx:=−14⇒ln(Γ(1−14))=γ4+∑k⩾2(ζ(k)k.4k)ln(Γ(34))−γ4=∑k⩾2(ζ(k)k.4k)

Commented by mindispower last updated on 15/May/21

sir are you student ?

sirareyoustudent?

Answered by Dwaipayan Shikari last updated on 15/May/21

ψ(z+1)=−γ+Σ_(n=2) ^∞ ζ(n)z^(n−1) [log(Γ(z+1))]_0 ^(−(1/4)) =−∫_0 ^((−1)/4) γ+Σ_(n=2) ^∞ ∫_0 ^(−(1/4)) (−1)^n ζ(n)z^(n−1) dz log(Γ((3/4)))=(γ/4)+Σ((ζ(n))/(n4^n )) Σ((ζ(n))/(n4^n ))=log(Γ((3/4)))−(γ/4)

ψ(z+1)=−γ+∑∞n=2ζ(n)zn−1[log(Γ(z+1))]0−14=−∫0−14γ+∑∞n=2∫0−14(−1)nζ(n)zn−1dzlog(Γ(34))=γ4+Σζ(n)n4nΣζ(n)n4n=log(Γ(34))−γ4

Commented by mnjuly1970 last updated on 15/May/21

very very nice thank you mr payan... taylor expansion of digamma..

veryverynicethankyoumrpayan...taylorexpansionofdigamma..

Terms of Service

Privacy Policy

Contact: info@tinkutara.com