Math Question and Answers


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 119570 by mnjuly1970 last updated on 25/Oct/20

$. . . \underset{♣}{\overset{♣}{♣}} n i c e c a l c u l u s \underset{♣}{\overset{♣}{♣}} . . .$ $p r o v e t h a t ::$ $Ω = \int_{0}^{\infty} e^{- 2 x} l n (\frac{1 + e^{- x}}{1 - e^{- x}}) = 1$ $. . . ★ M . N . 1970 ★ . . .$
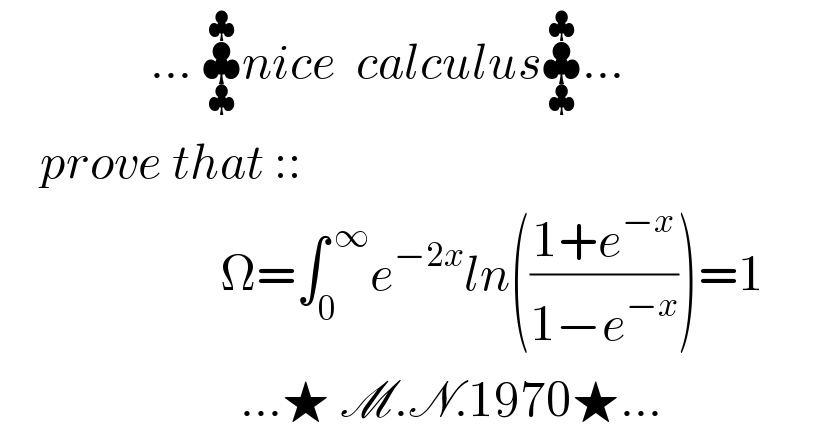
	Answered by mindispower last updated on 25/Oct/20

	$e^{- 2 x} = e^{- x} * e^{- x}$ $l e t t = e^{- x} \Rightarrow d t = - e^{- x} d x$ $\Leftrightarrow= \int_{0}^{1} t l n (\frac{1 + t}{1 - t}) d t = - \int_{0}^{1} t l n (\frac{1 - t}{1 + t}) d t$ $x = \frac{1 - t}{1 + t} \Rightarrow t = \frac{1 - x}{1 + x}, d t = \frac{- 2}{{(1 + x)}^{2}} d x$ $\Leftrightarrow - 2 \int_{0}^{1} \frac{1 - x}{{(1 + x)}^{3}} l n (x) d x$ $= - 2 {[(\frac{1}{(1 + x)} - \frac{1}{{(1 + x)}^{2}}) l n (x)]}_{0}^{1} + 2 \int (\frac{1}{(1 + x) x} - \frac{1}{x {(1 + x)}^{2}}) d x$ $= 2 \int_{0}^{1} \frac{1}{{(1 + x)}^{2}} = 2 {[- \frac{1}{(1 + x)}]}_{0}^{1} = 2 . \frac{1}{2} = 1$
	Commented by mnjuly1970 last updated on 25/Oct/20

	$t h a n k y o u m r p o w e r . .$
	Answered by mathmax by abdo last updated on 25/Oct/20
	$I =∫_0 ^∞ e^(−2x) ln(((1+e^(−x) )/(1−e^(−x) )))dx ⇒I =∫_0 ^∞ e^(−2x) ln(1+e^(−x) )dx−∫_0 ^∞ e^(−2x) ln(1−e^(−x) )dx =H−K H =∫_0 ^∞ e^(−2x) ln(1+e^(−x) )dx =_(e^(−x) =t) −∫_0 ^1 t^2 ln(1+t)(((−dt)/t))dt =∫_0 ^1 tln(1+t)dt =[(t^2 /2)ln(1+t)]_0 ^1 −∫_0 ^1 (t^2 /(2(1+t)))dt =((ln2)/2)−(1/2)∫_0 ^1 ((t^2 −1+1)/(t+1))dt =((ln2)/2)−(1/2){∫_0 ^1 (t−1)dt+∫_0 ^1 (dt/(t+1))} =((ln2)/2)−(1/2){[(t^2 /2)−t]_0 ^1 +ln(2)} =−(1/2)(−(1/2))=(1/4) K=∫_0 ^∞ e^(−2x) ln(1−e^(−x) )dx =_(e^(−x) =t) −∫_0 ^1 t^2 ln(1−t)(((−dt)/t)) =∫_0 ^1 tln(1−t)dt =[(1/2)(t^2 −1)ln(1−t)]_0 ^1 −∫_0 ^1 ((t^2 −1)/2)×((−1)/(1−t))dt =−(1/2)∫_0 ^1 (t+1)dt =−(1/2)[(t^2 /2)+t]_0 ^1 =−(1/2)((3/2))=−(3/4) ⇒ I =H−K =(1/4)+(3/4) ⇒ ★ I =1★$
	$I = \int_{0}^{\infty} e^{- 2 x} \ln (\frac{1 + e^{- x}}{1 - e^{- x}}) dx \Rightarrow I = \int_{0}^{\infty} e^{- 2 x} \ln (1 + e^{- x}) dx - \int_{0}^{\infty} e^{- 2 x} \ln (1 - e^{- x}) dx$ $= H - K$ $H = \int_{0}^{\infty} e^{- 2 x} \ln (1 + e^{- x}) dx =_{e^{- x} = t} - \int_{0}^{1} t^{2} \ln (1 + t) (\frac{- dt}{t}) dt$ $= \int_{0}^{1} tln (1 + t) dt = {[\frac{t^{2}}{2} \ln (1 + t)]}_{0}^{1} - \int_{0}^{1} \frac{t^{2}}{2 (1 + t)} dt$ $= \frac{\ln 2}{2} - \frac{1}{2} \int_{0}^{1} \frac{t^{2} - 1 + 1}{t + 1} dt = \frac{\ln 2}{2} - \frac{1}{2} {\int_{0}^{1} (t - 1) dt + \int_{0}^{1} \frac{dt}{t + 1}}$ $= \frac{\ln 2}{2} - \frac{1}{2} {{[\frac{t^{2}}{2} - t]}_{0}^{1} + \ln (2)} = - \frac{1}{2} (- \frac{1}{2}) = \frac{1}{4}$ $K = \int_{0}^{\infty} e^{- 2 x} \ln (1 - e^{- x}) dx =_{e^{- x} = t} - \int_{0}^{1} t^{2} \ln (1 - t) (\frac{- dt}{t})$ $= \int_{0}^{1} tln (1 - t) dt = {[\frac{1}{2} (t^{2} - 1) \ln (1 - t)]}_{0}^{1} - \int_{0}^{1} \frac{t^{2} - 1}{2} \times \frac{- 1}{1 - t} dt$ $= - \frac{1}{2} \int_{0}^{1} (t + 1) dt = - \frac{1}{2} {[\frac{t^{2}}{2} + t]}_{0}^{1} = - \frac{1}{2} (\frac{3}{2}) = - \frac{3}{4} \Rightarrow$ $I = H - K = \frac{1}{4} + \frac{3}{4} \Rightarrow ★ I = 1 ★$
	Commented by mnjuly1970 last updated on 25/Oct/20

	$t h a n k y o u m r m a x . .$
	Commented by Bird last updated on 25/Oct/20

	$y o u a r e w e l c o m e$
	Answered by mnjuly1970 last updated on 25/Oct/20

	Commented by mnjuly1970 last updated on 25/Oct/20

	$e d i t t i o n :$ $1 : r e c a l l :: l n (\frac{1 + z}{1 - z}) = 2 \underset{n = 0}{\sum^{\infty}} \frac{z^{2 n + 1}}{2 n + 1}$ $2 : Ω \overset{t e l e s c o p i c s e r i e s}{=} \frac{1}{2 (0) + 1} - {l i m}_{n \to \infty} (\frac{1}{2 n + 3}) = 1$ $. . . m . n . j u l y . 1970 . . .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum