
Question and Answers Forum
Question Number 68043 by mhmd last updated on 03/Sep/19
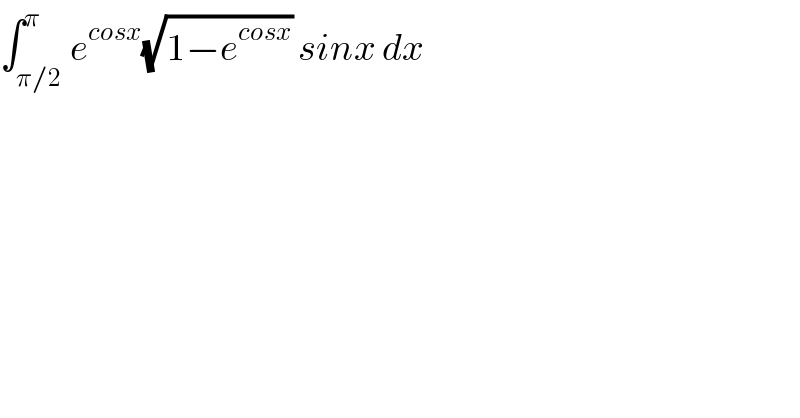
Commented by mathmax by abdo last updated on 03/Sep/19
![let I =∫_(π/2) ^π e^(cosx) (√(1−e^(cosx) ))sinx dx vha7gement cosx=−t give I =∫_0 ^1 e^(−t) (√(1−e^(−t) ))(dt) =∫_0 ^1 e^(−t) (√(1−e^(−t) ))dt after we do the changement (√(1−e_ ^(−t) ))=u ⇒1−e^(−t) =u^2 ⇒e^(−t) =1−u^2 ⇒ −t =ln(1−u^2 ) ⇒t =−ln(1−u^2 ) ⇒ I =∫_0 ^(√(1−e^(−1) )) (1−u^2 )u ×((2u)/(1−u^2 ))du =2 ∫_0 ^(√(1−e^(−1) )) u^(2 ) du =(2/3)[u^3 ]_0 ^(√(1−e^(−1) )) =(2/3){(√(1−e^(−1) ))}^3 =(2/3)(1−e^(−1) )(√(1−(1/e))) =(2/3)(1−(1/e))((√(e−1))/(√e)) =(2/3)(((e−1)/e))((√(e−1))/(√e)) ⇒ I =((2(e−1)(√(e−1)))/(3e(√e))) .](Q68053.png)
Answered by mr W last updated on 03/Sep/19
![=−∫_(π/2) ^π e^(cosx) (√(1−e^(cosx) )) d cos x =∫_(−1) ^0 e^t (√(1−e^t )) dt =∫_(−1) ^0 (√(1−e^t )) de^t =∫_(1/e) ^1 (√(1−u)) du =−∫_(1/e) ^1 (√(1−u)) d(1−u) =−(2/3)[(1−u)^(3/2) ]_(1/e) ^1 =(2/3)(1−(1/e))^(3/2)](Q68044.png)
| ||
Question and Answers Forum | ||
Question Number 68043 by mhmd last updated on 03/Sep/19 | ||
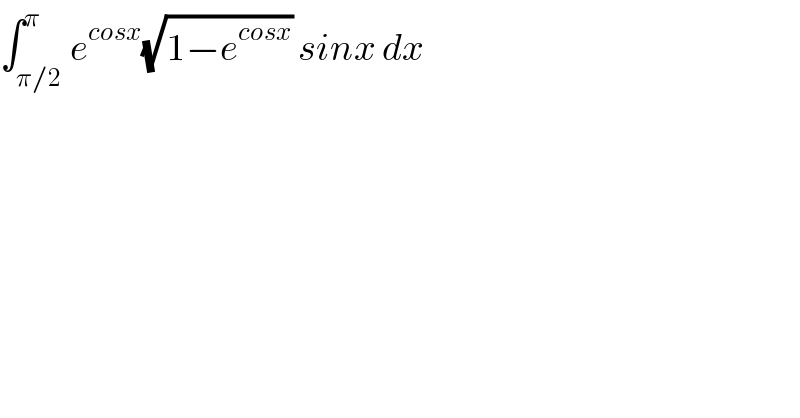 | ||
Commented by mathmax by abdo last updated on 03/Sep/19 | ||
![let I =∫_(π/2) ^π e^(cosx) (√(1−e^(cosx) ))sinx dx vha7gement cosx=−t give I =∫_0 ^1 e^(−t) (√(1−e^(−t) ))(dt) =∫_0 ^1 e^(−t) (√(1−e^(−t) ))dt after we do the changement (√(1−e_ ^(−t) ))=u ⇒1−e^(−t) =u^2 ⇒e^(−t) =1−u^2 ⇒ −t =ln(1−u^2 ) ⇒t =−ln(1−u^2 ) ⇒ I =∫_0 ^(√(1−e^(−1) )) (1−u^2 )u ×((2u)/(1−u^2 ))du =2 ∫_0 ^(√(1−e^(−1) )) u^(2 ) du =(2/3)[u^3 ]_0 ^(√(1−e^(−1) )) =(2/3){(√(1−e^(−1) ))}^3 =(2/3)(1−e^(−1) )(√(1−(1/e))) =(2/3)(1−(1/e))((√(e−1))/(√e)) =(2/3)(((e−1)/e))((√(e−1))/(√e)) ⇒ I =((2(e−1)(√(e−1)))/(3e(√e))) .](Q68053.png) | ||
Answered by mr W last updated on 03/Sep/19 | ||
![=−∫_(π/2) ^π e^(cosx) (√(1−e^(cosx) )) d cos x =∫_(−1) ^0 e^t (√(1−e^t )) dt =∫_(−1) ^0 (√(1−e^t )) de^t =∫_(1/e) ^1 (√(1−u)) du =−∫_(1/e) ^1 (√(1−u)) d(1−u) =−(2/3)[(1−u)^(3/2) ]_(1/e) ^1 =(2/3)(1−(1/e))^(3/2)](Q68044.png) | ||
| ||