
Question and Answers Forum
Question Number 128610 by john_santu last updated on 08/Jan/21
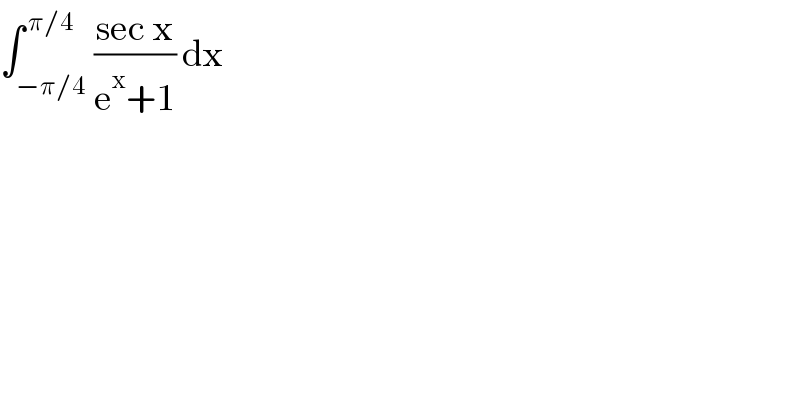
Commented by liberty last updated on 09/Jan/21
![I=−∫_(−π/4) ^( π/4) ((sec (−x))/(e^(−x) +1)) d(−x) I=∫_(−π/4) ^( π/4) ((sec x)/(e^(−x) +1))dx =∫ _(−π/4)^(π/4) (((sec x)/(e^(−x) (1+e^x ))))dx I=∫_(−π/4) ^( π/4) ((e^x sec x)/(e^x +1)) dx adding together two equation 2I=∫_(−π/4) ^( π/4) ((sec x+e^x sec x)/(e^x +1)) dx =∫_(−π/4) ^( π/4) sec x dx 2I = 2∫_0 ^( π/4) sec x dx I= ln ∣sec x+tan x∣ ]_( 0) ^(π/4) = ln (1+(√2) )](Q128635.png)
Answered by mathmax by abdo last updated on 09/Jan/21
![I=∫_(−(π/4)) ^(π/4) (1/(cosx(1+e^x )))dx =_(x=−t) ∫_(−(π/4)) ^(π/4) (1/(cost(1+e^(−t) )))dt ⇒ 2I =∫_(−(π/4)) ^(π/4) (1/(cosx))((1/(1+e^x ))+(1/(1+e^(−x) )))dx =∫_(−(π/4)) ^(π/4) (1/(cosx))(((1+e^(−x) +1+e^x )/(1+e^(−x) +e^x +1)))dx =∫_(−(π/4)) ^(π/4) (dx/(cosx)) =2∫_0 ^(π/4) (dx/(cosx)) ⇒ I =∫_0 ^(π/4) (dx/(cosx))=_(tan((x/2))=t) ∫_0 ^((√2)−1) ((2dt)/((1+t^2 ).((1−t^2 )/(1+t^2 )))) =∫_0 ^((√2)−1) ((1/(1−t))+(1/(1+t)))dt =[ln∣((1+t)/(1−t))∣]_0 ^((√2)−1) =ln∣((√2)/(2−(√2)))∣](Q128628.png)
| ||
Question and Answers Forum | ||
Question Number 128610 by john_santu last updated on 08/Jan/21 | ||
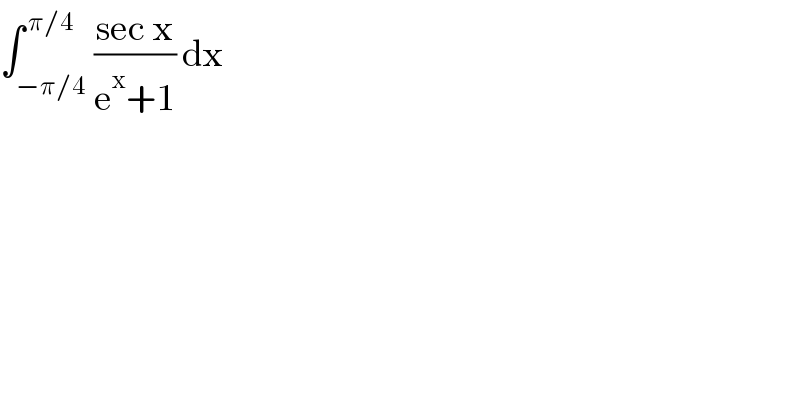 | ||
Commented by liberty last updated on 09/Jan/21 | ||
![I=−∫_(−π/4) ^( π/4) ((sec (−x))/(e^(−x) +1)) d(−x) I=∫_(−π/4) ^( π/4) ((sec x)/(e^(−x) +1))dx =∫ _(−π/4)^(π/4) (((sec x)/(e^(−x) (1+e^x ))))dx I=∫_(−π/4) ^( π/4) ((e^x sec x)/(e^x +1)) dx adding together two equation 2I=∫_(−π/4) ^( π/4) ((sec x+e^x sec x)/(e^x +1)) dx =∫_(−π/4) ^( π/4) sec x dx 2I = 2∫_0 ^( π/4) sec x dx I= ln ∣sec x+tan x∣ ]_( 0) ^(π/4) = ln (1+(√2) )](Q128635.png) | ||
Answered by mathmax by abdo last updated on 09/Jan/21 | ||
![I=∫_(−(π/4)) ^(π/4) (1/(cosx(1+e^x )))dx =_(x=−t) ∫_(−(π/4)) ^(π/4) (1/(cost(1+e^(−t) )))dt ⇒ 2I =∫_(−(π/4)) ^(π/4) (1/(cosx))((1/(1+e^x ))+(1/(1+e^(−x) )))dx =∫_(−(π/4)) ^(π/4) (1/(cosx))(((1+e^(−x) +1+e^x )/(1+e^(−x) +e^x +1)))dx =∫_(−(π/4)) ^(π/4) (dx/(cosx)) =2∫_0 ^(π/4) (dx/(cosx)) ⇒ I =∫_0 ^(π/4) (dx/(cosx))=_(tan((x/2))=t) ∫_0 ^((√2)−1) ((2dt)/((1+t^2 ).((1−t^2 )/(1+t^2 )))) =∫_0 ^((√2)−1) ((1/(1−t))+(1/(1+t)))dt =[ln∣((1+t)/(1−t))∣]_0 ^((√2)−1) =ln∣((√2)/(2−(√2)))∣](Q128628.png) | ||
| ||