Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 158405 by Eric002 last updated on 03/Nov/21

$$prove:$$$${\int }_0^{\mathrm{\infty }}\frac{1}{x^5+x^4+x^3+x^2+x+1}dx=\frac{\pi }{3\sqrt{3}}$$

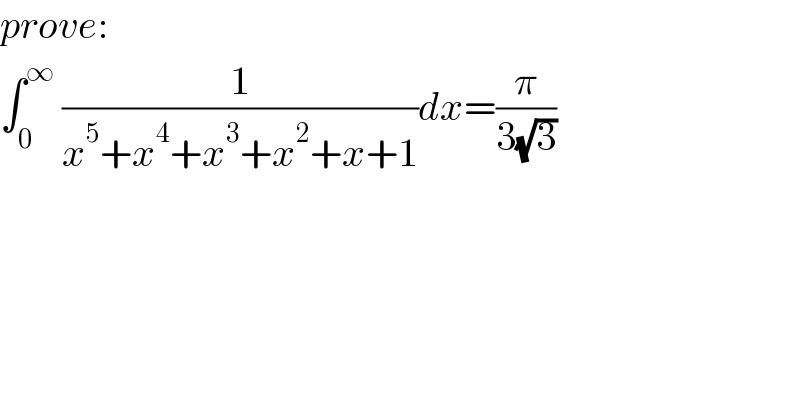
Answered by MJS_new last updated on 03/Nov/21

$$x^5+x^4+x^3+x^2+x+1=\frac{x^6-1}{x-1}$$$$\Rightarrow$$$$\int \frac{dx}{x^5+x^4+x^3+x^2+x+1}=$$$$=\int \frac{dx}{(x+1)(x^2+x+1)(x^2+x+1)}=$$$$=\frac{1}{3}\int \frac{dx}{x+1}+\frac{1}{2}\int \frac{dx}{x^2+x+1}-\frac{1}{6}\int \frac{2x-1}{x^2-x+1}=$$$$=\frac{1}{3}\ln \mid x+1\mid +\frac{\sqrt{3}}{3}\arctan \frac{2x+1}{\sqrt{3}}-\frac{1}{6}\ln (x^2-x+1)+C$$$$\Rightarrow$$$$\underset{0}{\stackrel{\mathrm{\infty }}{\int }}\frac{dx}{x^5+x^4+x^3+x^2+x+1}=\frac{\pi }{3\sqrt{3}}$$

Commented by Eric002 last updated on 03/Nov/21

$$welldone$$

Commented by Tawa11 last updated on 04/Nov/21

$$\mathrm{Great}\mathrm{sir}$$

Answered by Ar Brandon last updated on 03/Nov/21

$$I={\int }_0^{\mathrm{\infty }}\frac{dx}{x^5+x^4+x^3+x^2+x+1}={\int }_0^{\mathrm{\infty }}\frac{1-x}{1-x^6}dx$$$$={\int }_0^1\frac{1-x}{1-x^6}dx+{\int }_1^{\mathrm{\infty }}\frac{1-x}{1-x^6}dx={\int }_0^1\frac{1-x}{1-x^6}dx+{\int }_0^1\frac{x^3-x^4}{1-x^6}dx$$$$={\int }_0^1\frac{1-x+x^3-x^4}{1-x^6}dx=\frac{1}{6}{\int }_0^1\frac{{\mathrm{v}}^{-\frac{5}{6}}-{\mathrm{v}}^{-\frac{4}{6}}+{\mathrm{v}}^{-\frac{2}{6}}-{\mathrm{v}}^{-\frac{1}{6}}}{1-\mathrm{v}}d\mathrm{v}$$$$=\frac{1}{6}[-\psi \left(\frac{1}{6}\right)+\psi \left(\frac{2}{6}\right)-\psi \left(\frac{4}{6}\right)+\psi \left(\frac{5}{6}\right)]$$$$=\frac{1}{6}[(\psi \left(\frac{5}{6}\right)-\psi \left(\frac{1}{6}\right))+(\psi \left(\frac{1}{3}\right)-\psi \left(\frac{2}{3}\right))]$$$$=\frac{1}{6}[-\pi \cot \left(\frac{5}{6}\pi \right)-\pi \cot \left(\frac{\pi }{3}\right)]=\frac{1}{6}[\pi \sqrt{3}-\frac{\pi }{\sqrt{3}}]=\frac{2\sqrt{3}\pi }{18}=\frac{\sqrt{3}}{9}\pi$$

Commented by Ar Brandon last updated on 03/Nov/21

$$\mathrm{\Phi }={\int }_1^{\mathrm{\infty }}\frac{1-x}{1-x^6}dx,u=\frac{1}{x}\Rightarrow x=\frac{1}{u}\Rightarrow dx=-\frac{1}{u^2}du$$$$\Rightarrow \mathrm{\Phi }={\int }_0^1\frac{1-\frac{1}{u}}{1-\frac{1}{u^6}}\cdot \frac{du}{u^6}={\int }_0^1\frac{u^4-u^3}{u^6-1}du={\int }_0^1\frac{x^3-x^4}{1-x^6}dx$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com