
Question and Answers Forum
Question Number 150747 by mnjuly1970 last updated on 15/Aug/21
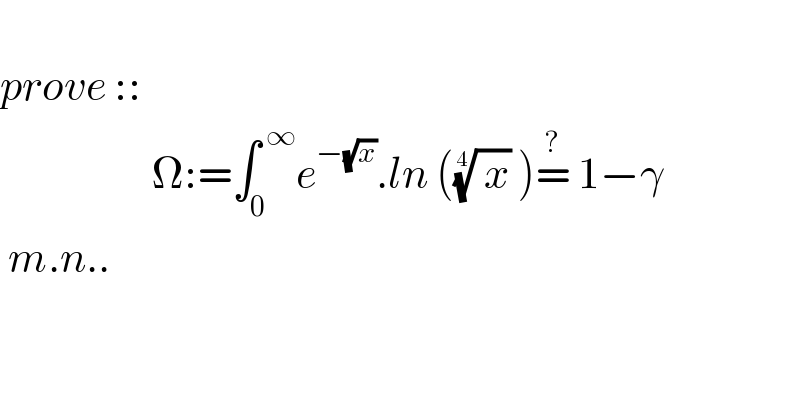
Answered by Olaf_Thorendsen last updated on 15/Aug/21
![Ω = ∫_0 ^∞ e^(−(√x)) ln((x)^(1/4) ) dx Ω = ∫_0 ^∞ e^(−u) ln((√u)) (2udu) Ω = ∫_0 ^∞ ue^(−u) lnu du ψ(z) = ((∫_0 ^∞ y^(z−1) lny e^(−y) dy)/(∫_0 ^∞ y^(z−1) e^(−y) dy)) ψ(2) = ((∫_0 ^∞ y.lny e^(−y) dy)/(∫_0 ^∞ ye^(−y) dy)) = (Ω/(∫_0 ^∞ ye^(−y) dy)) ∫_0 ^∞ ue^(−u) du = [−ue^(−u) ]_0 ^∞ +∫_0 ^∞ e^(−u) du = 1 ⇒ Ω = ψ(2) ψ(z+1) = ψ(z)+(1/z) ψ(2) = ψ(1)+(1/1) = −γ+1 Ω = 1−γ = ψ(2)](Q150760.png)
Commented by mnjuly1970 last updated on 16/Aug/21

Answered by mathmax by abdo last updated on 17/Aug/21
![Ψ=∫_0 ^∞ e^(−(√x)) ln(x^(1/4) )dx ⇒Ψ=_((√x)=t) ∫_0 ^∞ e^(−t) ln(t^(1/2) )(2t)dt =2∫_0 ^∞ (t/2)ln(t)e^(−t) dt =∫_0 ^∞ te^(−t) ln(t)dt =∫_0 ^∞ (tlnt)e^(−t) dt by parts u=tlnt and v^(′ ) =e^(−t) =[−e^(−t) (tlnt)]_0 ^∞ −∫_0 ^∞ (lnt+1)(−e^(−t) )dt =0+∫_0 ^∞ e^(−t) (1+lnt)dt =∫_0 ^∞ e^(−t) dt +∫_0 ^∞ e^(−t) lnt dt =1−γ](Q150958.png)
| ||
Question and Answers Forum | ||
Question Number 150747 by mnjuly1970 last updated on 15/Aug/21 | ||
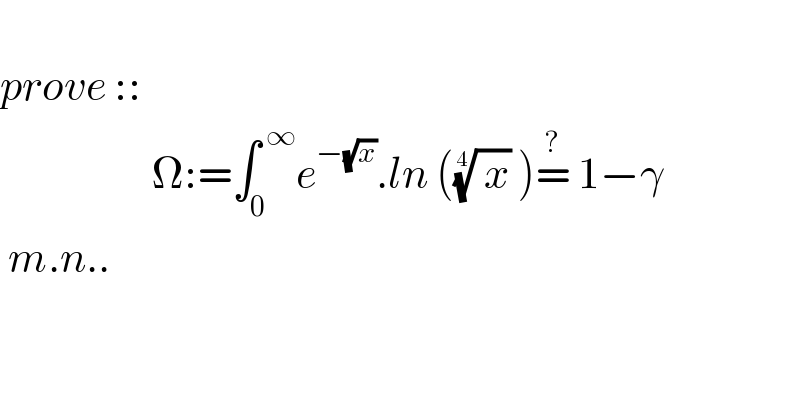 | ||
Answered by Olaf_Thorendsen last updated on 15/Aug/21 | ||
![Ω = ∫_0 ^∞ e^(−(√x)) ln((x)^(1/4) ) dx Ω = ∫_0 ^∞ e^(−u) ln((√u)) (2udu) Ω = ∫_0 ^∞ ue^(−u) lnu du ψ(z) = ((∫_0 ^∞ y^(z−1) lny e^(−y) dy)/(∫_0 ^∞ y^(z−1) e^(−y) dy)) ψ(2) = ((∫_0 ^∞ y.lny e^(−y) dy)/(∫_0 ^∞ ye^(−y) dy)) = (Ω/(∫_0 ^∞ ye^(−y) dy)) ∫_0 ^∞ ue^(−u) du = [−ue^(−u) ]_0 ^∞ +∫_0 ^∞ e^(−u) du = 1 ⇒ Ω = ψ(2) ψ(z+1) = ψ(z)+(1/z) ψ(2) = ψ(1)+(1/1) = −γ+1 Ω = 1−γ = ψ(2)](Q150760.png) | ||
| ||
Commented by mnjuly1970 last updated on 16/Aug/21 | ||
 | ||
Answered by mathmax by abdo last updated on 17/Aug/21 | ||
![Ψ=∫_0 ^∞ e^(−(√x)) ln(x^(1/4) )dx ⇒Ψ=_((√x)=t) ∫_0 ^∞ e^(−t) ln(t^(1/2) )(2t)dt =2∫_0 ^∞ (t/2)ln(t)e^(−t) dt =∫_0 ^∞ te^(−t) ln(t)dt =∫_0 ^∞ (tlnt)e^(−t) dt by parts u=tlnt and v^(′ ) =e^(−t) =[−e^(−t) (tlnt)]_0 ^∞ −∫_0 ^∞ (lnt+1)(−e^(−t) )dt =0+∫_0 ^∞ e^(−t) (1+lnt)dt =∫_0 ^∞ e^(−t) dt +∫_0 ^∞ e^(−t) lnt dt =1−γ](Q150958.png) | ||
| ||