
Question and Answers Forum
Question Number 106816 by bemath last updated on 07/Aug/20

Commented by bobhans last updated on 07/Aug/20
![(2)n^2 +2n+1< 2n^2 ; 2n+1 < n^2 ; n≥3 P_1 (n=3)⇒2.3+1<3^2 [ true ] let :P_k (n=k,k≥3)⇒2k+1 < k^2 [true] P_(k+1) (n=k+1)⇒LHS : 2(k+1)+1 = 2k+3 = (2k+1)+2 < k^2 +2 =k^2 −2k+1+(1+2k) =(k+1)^2 +2k+1 =](Q106820.png)
Answered by bobhans last updated on 07/Aug/20
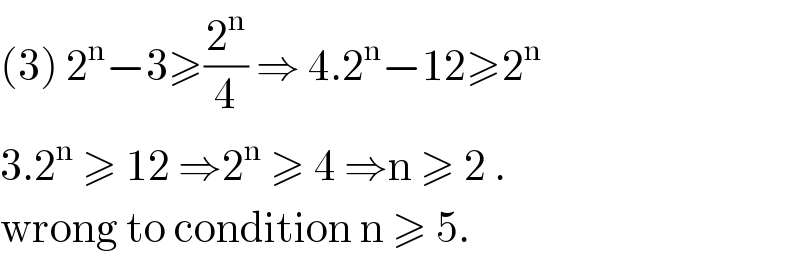
Answered by Rio Michael last updated on 07/Aug/20

| ||
Question and Answers Forum | ||
Question Number 106816 by bemath last updated on 07/Aug/20 | ||
 | ||
Commented by bobhans last updated on 07/Aug/20 | ||
![(2)n^2 +2n+1< 2n^2 ; 2n+1 < n^2 ; n≥3 P_1 (n=3)⇒2.3+1<3^2 [ true ] let :P_k (n=k,k≥3)⇒2k+1 < k^2 [true] P_(k+1) (n=k+1)⇒LHS : 2(k+1)+1 = 2k+3 = (2k+1)+2 < k^2 +2 =k^2 −2k+1+(1+2k) =(k+1)^2 +2k+1 =](Q106820.png) | ||
Answered by bobhans last updated on 07/Aug/20 | ||
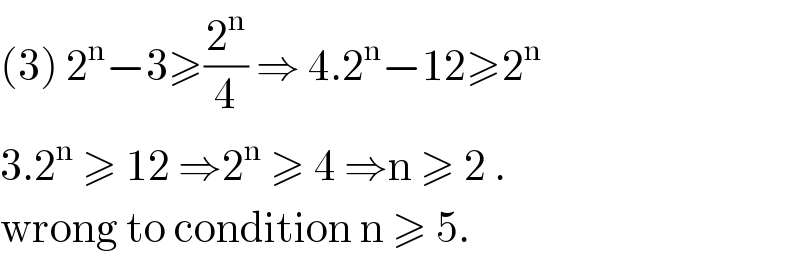 | ||
| ||
Answered by Rio Michael last updated on 07/Aug/20 | ||
 | ||
| ||