
Question and Answers Forum
Question Number 38118 by maxmathsup by imad last updated on 21/Jun/18
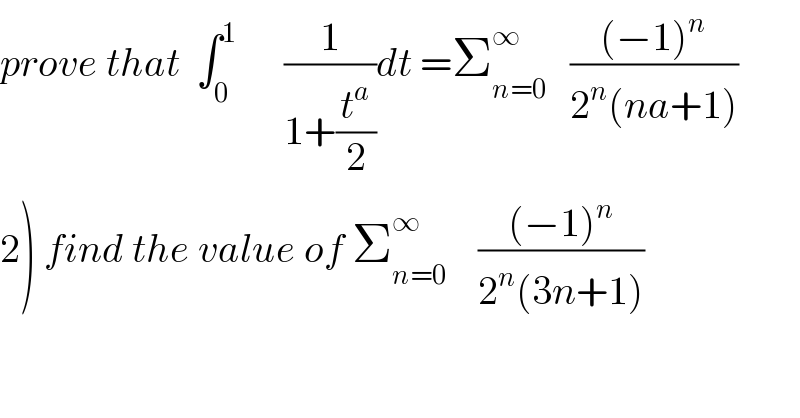
Commented by abdo mathsup 649 cc last updated on 05/Jul/18
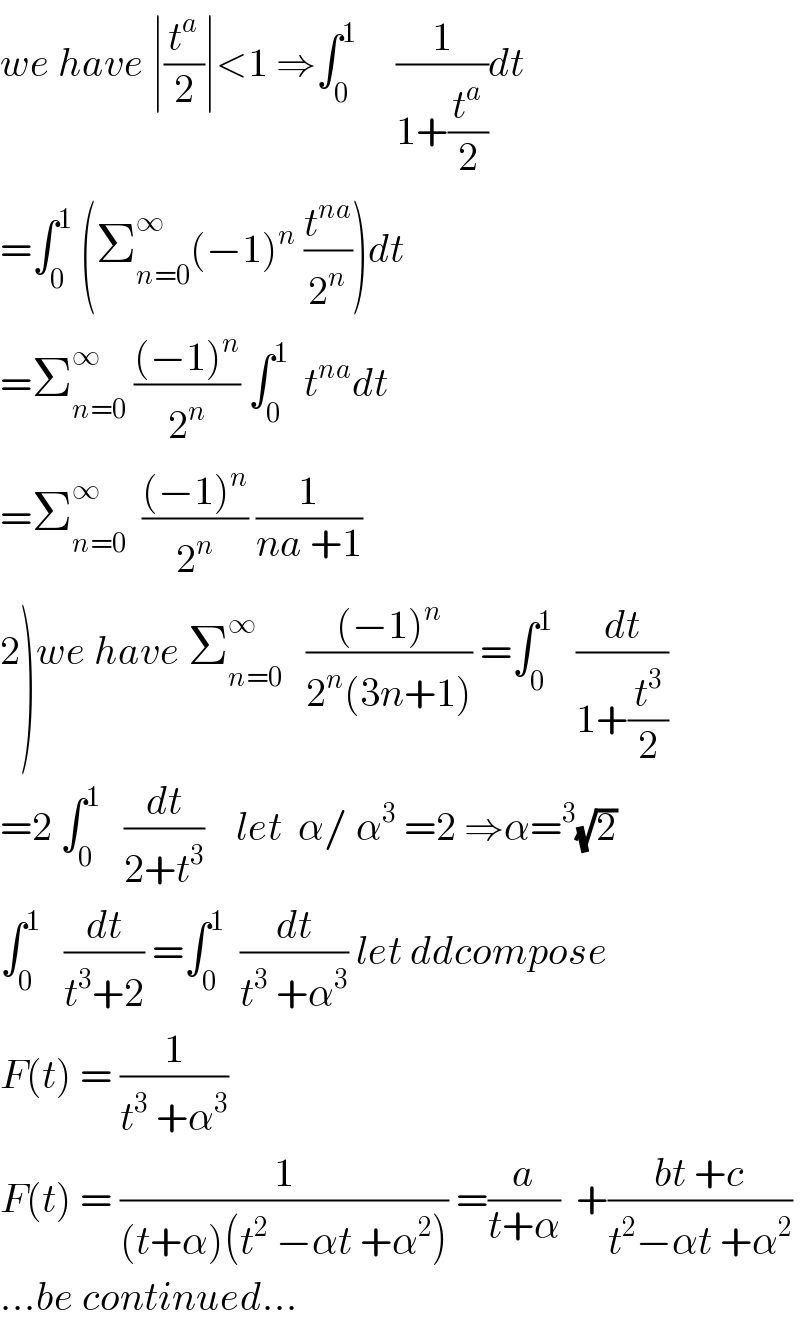
| ||
Question and Answers Forum | ||
Question Number 38118 by maxmathsup by imad last updated on 21/Jun/18 | ||
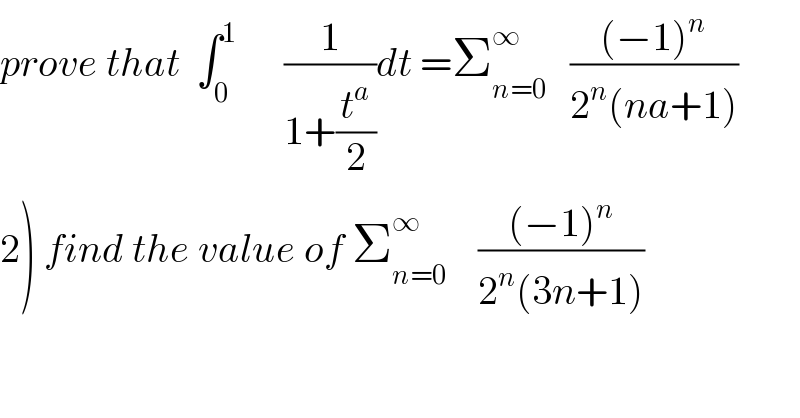 | ||
Commented by abdo mathsup 649 cc last updated on 05/Jul/18 | ||
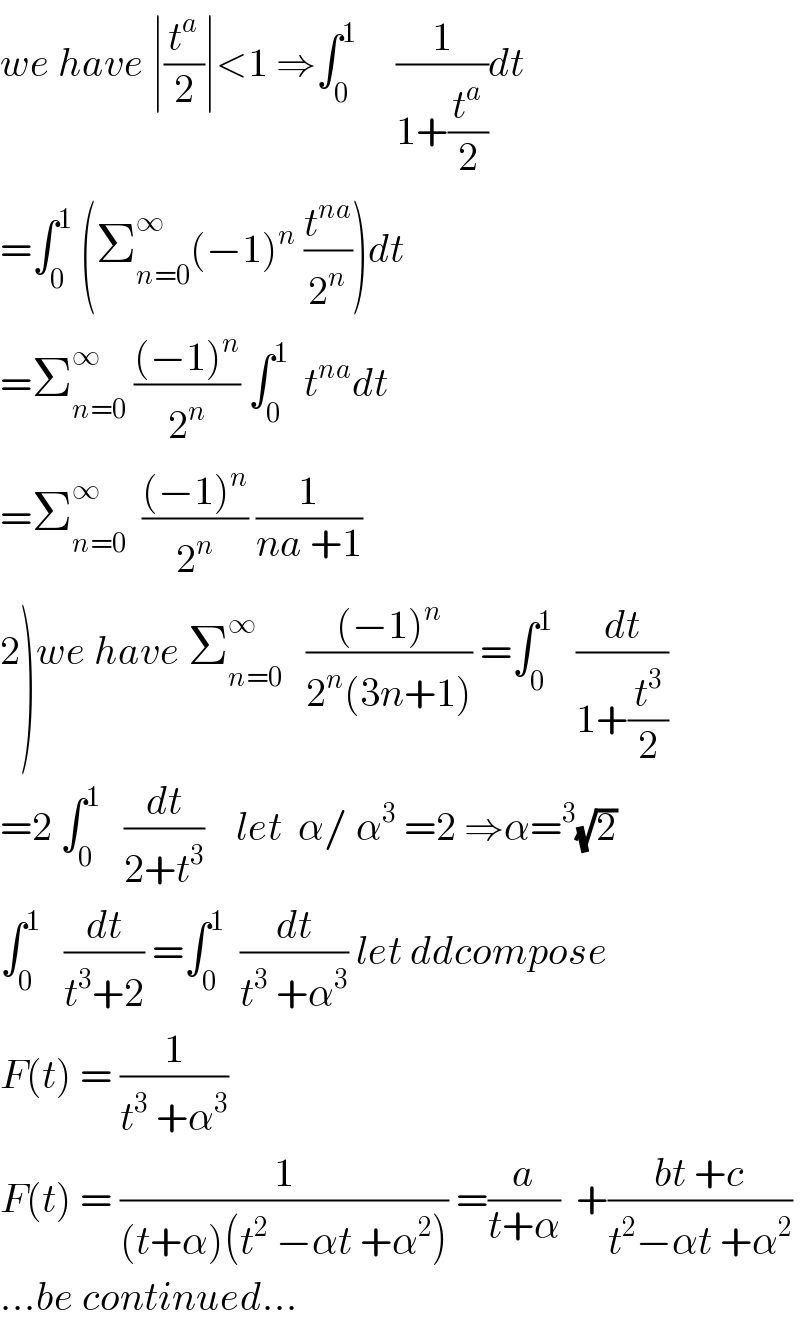 | ||