
Question and Answers Forum
Question Number 40889 by abdo.msup.com last updated on 28/Jul/18
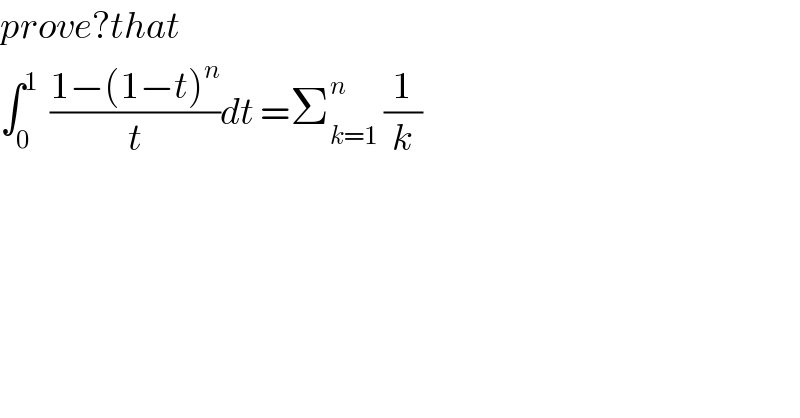
Answered by math khazana by abdo last updated on 30/Jul/18
![we have 1−x^n =(1−x)(1+x+x^2 +...+x^(n−1) )⇒ ((1−(1−t)^n )/t) =((t(1+(1−t)+(1−t)^2 +...+(1−t)^(n−1) )/t) ∫_0 ^1 ((1−(1−t))/t)dt =∫_0 ^1 Σ_(k=0) ^(n−1) (1−t)^k dt =Σ_(k=0) ^(n−1) ∫_0 ^1 (1−t)^k dt =Σ_(k=0) ^n [−(1/(k+1))(1−t)^(k+1) ]_0 ^1 =Σ_(k=0) ^(n−1) (1/(k+1)) =Σ_(k=1) ^n (1/k) (=H_n ).](Q40951.png)
| ||
Question and Answers Forum | ||
Question Number 40889 by abdo.msup.com last updated on 28/Jul/18 | ||
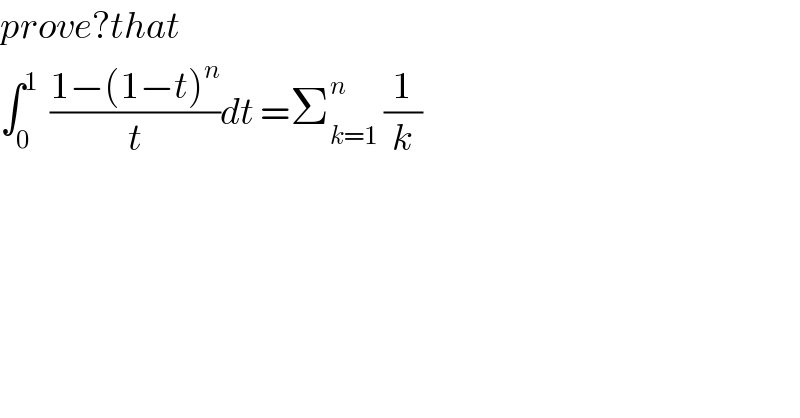 | ||
Answered by math khazana by abdo last updated on 30/Jul/18 | ||
![we have 1−x^n =(1−x)(1+x+x^2 +...+x^(n−1) )⇒ ((1−(1−t)^n )/t) =((t(1+(1−t)+(1−t)^2 +...+(1−t)^(n−1) )/t) ∫_0 ^1 ((1−(1−t))/t)dt =∫_0 ^1 Σ_(k=0) ^(n−1) (1−t)^k dt =Σ_(k=0) ^(n−1) ∫_0 ^1 (1−t)^k dt =Σ_(k=0) ^n [−(1/(k+1))(1−t)^(k+1) ]_0 ^1 =Σ_(k=0) ^(n−1) (1/(k+1)) =Σ_(k=1) ^n (1/k) (=H_n ).](Q40951.png) | ||
| ||