Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 162535 by mnjuly1970 last updated on 30/Dec/21

$$$$$$\mathrm{prove}\mathrm{that}$$$$\mathrm{\Omega }={\int }_0^{\mathrm{\infty }}\frac{\ln \left(\frac{1}{x}\right)}{x^4+17x^2+16}dx\stackrel{?}{=}\frac{\pi }{60}\ln \left(2\right)$$$$$$

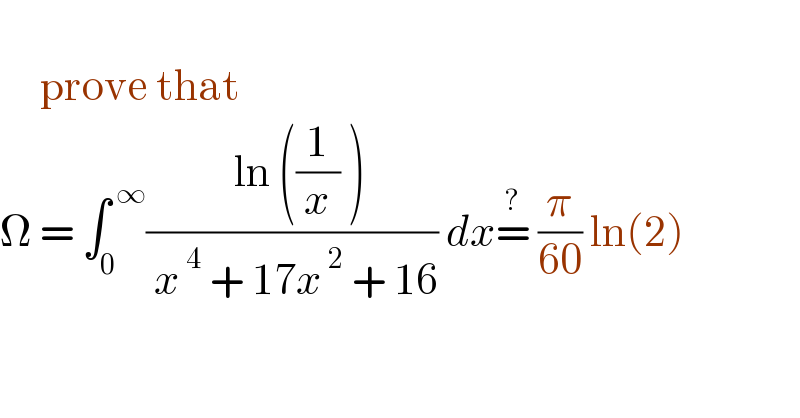
Commented by Ar Brandon last updated on 30/Dec/21

$$\mathrm{Synthax}\mathrm{error},\mathrm{Sir}.\mathrm{Your}dx\mathrm{is}\mathrm{missing}.$$Haha 😅😁

Commented by amin96 last updated on 30/Dec/21

$$$$very big mistake😂😂

Commented by mnjuly1970 last updated on 30/Dec/21

$$yesyouarerightsir...$$

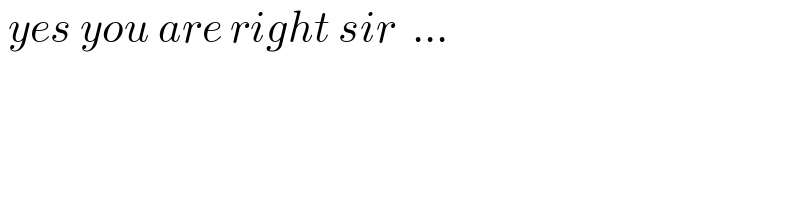
Answered by Ar Brandon last updated on 24/Mar/22

$$\mathrm{\Omega }={\int }_0^{\mathrm{\infty }}\frac{\ln \left(\frac{1}{x}\right)}{x^4+17x^2+16}dx=-{\int }_0^{\mathrm{\infty }}\frac{\ln x}{x^4+17x^2+16}dx$$$$\phi \left(z\right)=\frac{{\left(\ln z\right)}^2}{z^4+17z^2+16},\mathrm{poles}:(z^2+16)(z^2+1)=0\Rightarrow z_1=4e^{\frac{\pi }{2}i},z_2=4e^{-\frac{\pi }{2}i},z_3=e^{\frac{\pi }{2}i},z_4=e^{-\frac{\pi }{2}i}$$$$\mathrm{\Omega }=-\frac{1}{2}Re(Res(\phi ,z_1)+Res(\phi ,z_2)+Res(\phi ,z_3)+Res(\phi ,z_4))$$$$Res(\phi ,z_1)=\underset{z\to z_1}{\lim }\left(\frac{{\left(\ln z\right)}^2}{(z-z_2)(z-z_3)(z-z_4)}\right)=\frac{{(\ln 4+\frac{\pi }{2}i)}^2}{\left(8i\right)\left(3i\right)\left(5i\right)}=\frac{i}{120}({\ln }^{2}4-\frac{{\pi }^2}{4}+i\pi \ln 4)$$$$Res(\phi ,z_2)=\underset{z\to z_2}{\lim }\left(\frac{{\left(\ln z\right)}^2}{(z-z_1)(z-z_3)(z-z_4)}\right)=\frac{{(\ln 4-\frac{\pi }{2}i)}^2}{(-8i)(-5i)(-3i)}=-\frac{i}{120}({\ln }^{2}4+\frac{{\pi }^2}{4}-i\pi \ln 4)$$$$Res(\phi ,z_3)=\underset{z\to z_3}{\lim }\left(\frac{{\left(\ln z\right)}^2}{(z-z_1)(z-z_2)(z-z_4)}\right)=\frac{{\left(\frac{\pi }{2}i\right)}^2}{(-3i)\left(5i\right)\left(2i\right)}=\frac{i}{30}\left(\frac{{\pi }^2}{4}\right)=i\frac{{\pi }^2}{120}$$$$Res(\phi ,z_4)=\underset{z\to z_4}{\lim }\left(\frac{{\left(\ln z\right)}^2}{(z-z_1)(z-z_2)(z-z_3)}\right)=\frac{{(-\frac{\pi }{2}i)}^2}{(-5i)\left(3i\right)(-2i)}=-\frac{i}{30}\left(\frac{{\pi }^2}{4}\right)=-i\frac{{\pi }^2}{120}$$$$\mathrm{\Omega }=-\frac{1}{2}(-\frac{\pi \ln 4}{120}-\frac{\pi \ln 4}{120})=\frac{\pi \ln 4}{120}=\frac{\pi }{60}\ln \left(2\right)$$

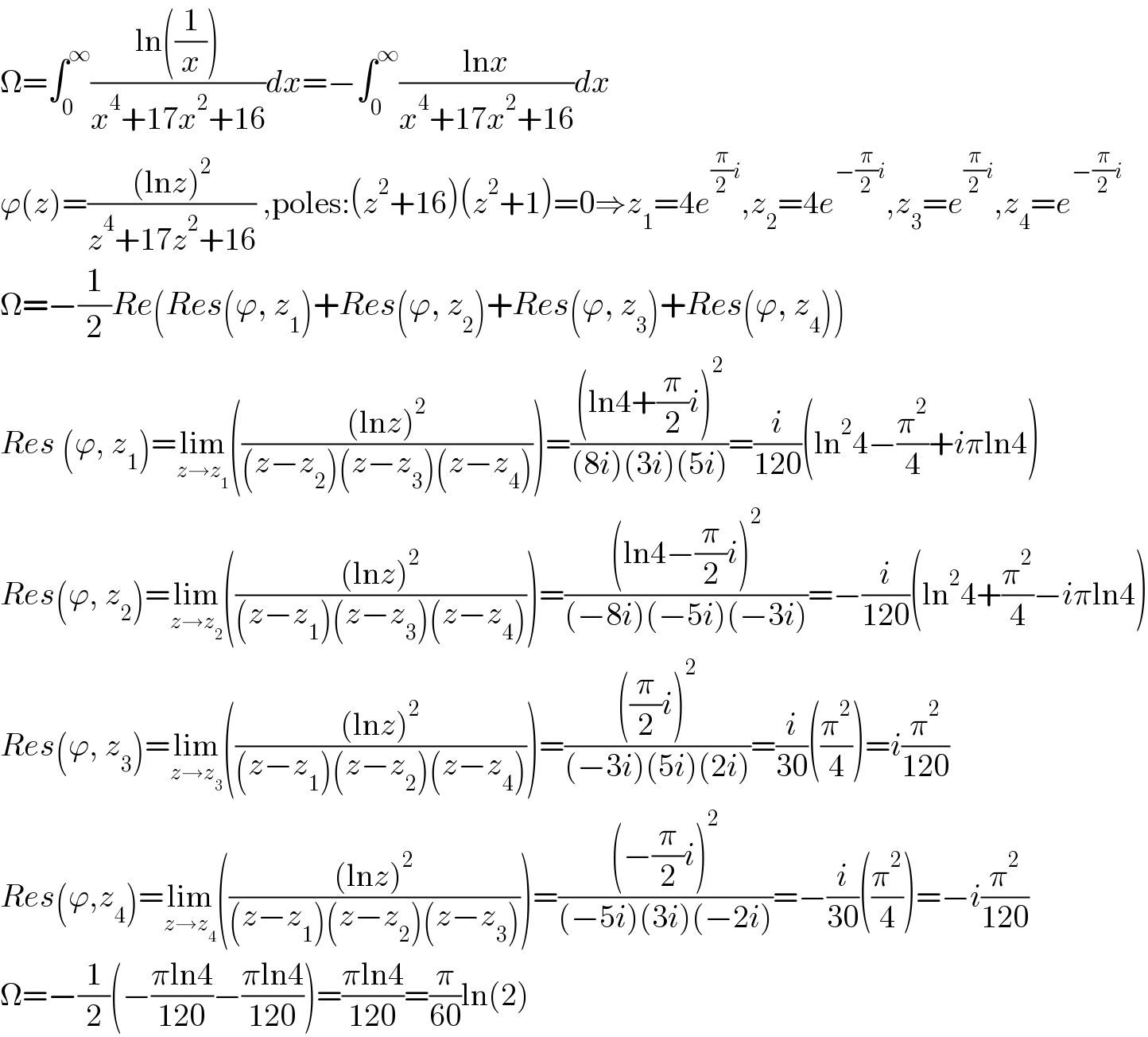
Commented by mnjuly1970 last updated on 30/Dec/21

$$verynicesolution..residuestheory..$$$$thanksalotsirbrandon..$$

Answered by mindispower last updated on 30/Dec/21

$$=-{\int }_0^{\mathrm{\infty }}-\frac{ln\left(x\right)}{(x^2+16)(x^2+1)}dx=-\frac{1}{15}{\int }_0^{\mathrm{\infty }}\frac{ln\left(x\right)}{x^2+1}+\frac{ln\left(x\right)}{x^2+16}dx$$$$=\frac{1}{15}(-{\int }_0^{\mathrm{\infty }}\frac{ln\left(x\right)}{x^2+1}dx+\int \frac{ln\left(4y\right)}{16(y^2+1)}4y$$$$=-\frac{3}{60}{\int }_0^{\mathrm{\infty }}\frac{ln\left(x\right)}{1+x^2}+\frac{ln\left(4\right)}{60}{\int }_0^{\mathrm{\infty }}\frac{dx}{1+x^2}$$$${\int }_0^{\mathrm{\infty }}\frac{ln\left(x\right)}{1+x^2}dx,x\to \frac{1}{x}\Rightarrow =-{\int }_0^{\mathrm{\infty }}\frac{ln\left(x\right)}{1+x^2}dx$$$$\Rightarrow {\int }_0^{\mathrm{\infty }}\frac{ln\left(x\right)}{1+x^2}dx=0$$$$\mathrm{\Omega }=\frac{\ln \left(4\right)}{60}{\int }_0^{\mathrm{\infty }}\frac{dx}{1+x^2}=\frac{ln\left(4\right)}{60}\underset{x\to \mathrm{\infty }}{\lim }{\left[{\tan }^{-1}\left(z\right)\right]}_0^x$$$$=\frac{ln\left(4\right)}{60}.\frac{\pi }{2}=\frac{\pi ln\left(2\right)}{60}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com