
Question and Answers Forum
Question Number 26242 by abdo imad last updated on 22/Dec/17
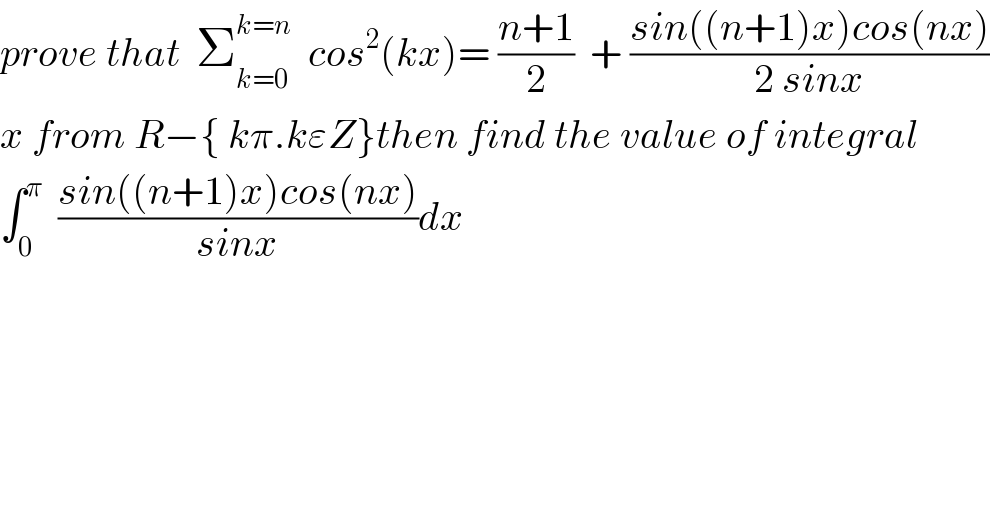
Commented by abdo imad last updated on 28/Dec/17
![Σ_(k=0) ^(k=n) cos^2 (kx)=(1/2) Σ_(k=0) ^(k=n ) (1+cos(2kx)) = ((n+1)/2)+ (1/2) Σ_(k=0) ^n cos(2kx) but Σ_(k=0) ^(k=n) cos(2kx) =Re( Σ_(k=0) ^(k=n) e^(i2kx) ) = Re(((1−e^(i2(n+1)x) )/(1− e^(i2x) ))) but ((1−e^(i2(n+1)x) )/(1−e^(i2x) )) = ((1−cos2(n+1)x −isin(2(n+1)x))/(1 −cos(2x)−isin(2x))) =(( 2sin^2 (n+1)x −2isin(n+1)x cos(n+1)x)/(2sin^2 x −2i sinx cosx)) = ((−isin(n+1)x( cos(n+1)x +isin(n+1)x))/(−isinx( cosx +i sinx))) = ((sin(n+1)x)/(sinx)) e^(i(n+1)x) e^(−ix) = ((sin(n+1)x)/(sinx)) e^(inx) = ((sin(n+1)x)/(sinx))cos(nx) +i ((sin(n+1)x sin(nx))/(sinx)) ⇒ Re( Σ_(k=0) ^(k=n) e^(i2kx) )= ((sin(n+1)x cos(nx))/(sinx)) ⇒ Σ_(k=0) ^(k=n) cos^2 (kx)= ((n+1)/2)+ ((sin(n+1)x cos(nx))/(2sinx)) ∫_0 ^π ((sin(n+1)x cos(nx))/(2sinx))dx= Σ_(k=>) ^n ∫_0 ^π cos^2 (kx)dx−(((n+1)π)/2) = (1/2)Σ_(k=0) ^(k=n) ∫_0 ^π (1+ cos(2kx))dx −(((n+1)π)/2) = (1/2) Σ_(k=0) ^(k=n) ∫_0 ^π cos(2kx)dx = (π/2)+ Σ_(k=1) ^(k=n) [(1/(2k)) sin(2kx)]_(k=0) ^(k=π=) =(π/2) +0 = (π/2)⇒ ∫_0 ^π ((sin(n+1)x cos(nx))/(sinx))dx =π](Q26754.png)
| ||
Question and Answers Forum | ||
Question Number 26242 by abdo imad last updated on 22/Dec/17 | ||
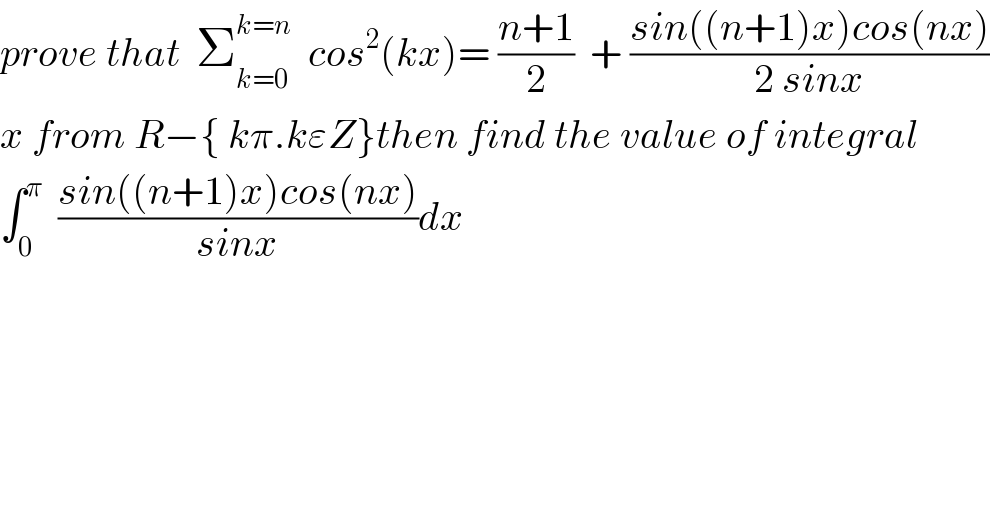 | ||
Commented by abdo imad last updated on 28/Dec/17 | ||
![Σ_(k=0) ^(k=n) cos^2 (kx)=(1/2) Σ_(k=0) ^(k=n ) (1+cos(2kx)) = ((n+1)/2)+ (1/2) Σ_(k=0) ^n cos(2kx) but Σ_(k=0) ^(k=n) cos(2kx) =Re( Σ_(k=0) ^(k=n) e^(i2kx) ) = Re(((1−e^(i2(n+1)x) )/(1− e^(i2x) ))) but ((1−e^(i2(n+1)x) )/(1−e^(i2x) )) = ((1−cos2(n+1)x −isin(2(n+1)x))/(1 −cos(2x)−isin(2x))) =(( 2sin^2 (n+1)x −2isin(n+1)x cos(n+1)x)/(2sin^2 x −2i sinx cosx)) = ((−isin(n+1)x( cos(n+1)x +isin(n+1)x))/(−isinx( cosx +i sinx))) = ((sin(n+1)x)/(sinx)) e^(i(n+1)x) e^(−ix) = ((sin(n+1)x)/(sinx)) e^(inx) = ((sin(n+1)x)/(sinx))cos(nx) +i ((sin(n+1)x sin(nx))/(sinx)) ⇒ Re( Σ_(k=0) ^(k=n) e^(i2kx) )= ((sin(n+1)x cos(nx))/(sinx)) ⇒ Σ_(k=0) ^(k=n) cos^2 (kx)= ((n+1)/2)+ ((sin(n+1)x cos(nx))/(2sinx)) ∫_0 ^π ((sin(n+1)x cos(nx))/(2sinx))dx= Σ_(k=>) ^n ∫_0 ^π cos^2 (kx)dx−(((n+1)π)/2) = (1/2)Σ_(k=0) ^(k=n) ∫_0 ^π (1+ cos(2kx))dx −(((n+1)π)/2) = (1/2) Σ_(k=0) ^(k=n) ∫_0 ^π cos(2kx)dx = (π/2)+ Σ_(k=1) ^(k=n) [(1/(2k)) sin(2kx)]_(k=0) ^(k=π=) =(π/2) +0 = (π/2)⇒ ∫_0 ^π ((sin(n+1)x cos(nx))/(sinx))dx =π](Q26754.png) | ||