
Question and Answers Forum
Question Number 5490 by 123456 last updated on 16/May/16
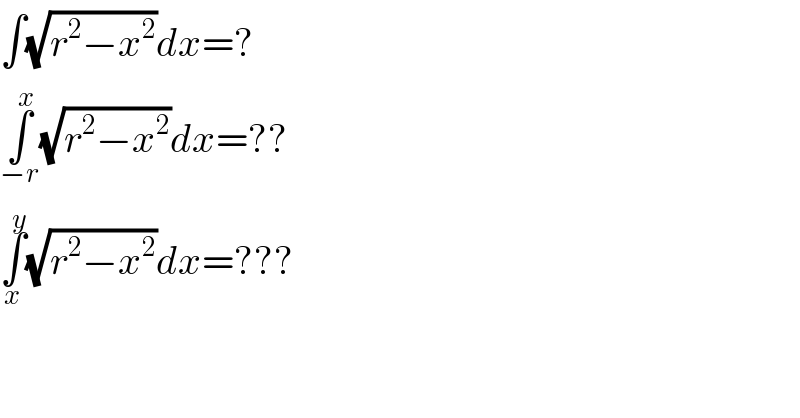
Answered by FilupSmith last updated on 16/May/16
![let x=r∙sin(θ) ⇒ dx=cos(θ)dθ ∴θ=arcsin((x/r)) ∴∫(√(r^2 −x^2 ))dx=∫((√(r^2 −r^2 sin^2 θ ))cosθ)dθ =∫cosθ(√(r^2 (1−sin^2 θ)))dθ =∫rcosθ(√(cos^2 θ))dθ =r∫cos^2 θdθ cos^2 (x)=((cos(2x)+1)/2) =r∫(1/2)(cos(2θ)+1)dθ =(r/2)((1/2)sin(2θ)+θ)+c ∴∫(√(r^2 −x^2 ))dx=(1/4)r∙sin(2∙arcsin((x/r)))+(1/2)r∙arcsin((x/r))+c −−−−−−−−−−−−−− ∫_(−r) ^x (√(r^2 −x^2 ))dx=(r/2)[(1/2)sin(2∙arcsin((x/r)))+arcsin((x/r))]_(−r) ^x =(r/2)[(1/2)sin(2∙arcsin((x/r)))+arcsin((x/r))−(1/2)sin(2∙arcsin(((−r)/r)))+r∙arcsin(((−r)/r))] =(r/2)[(1/2)sin(2∙arcsin((x/r)))+r∙arcsin((x/r))−(1/2)sin(−π)+(π/2)] ∴∫_(−r) ^x (√(r^2 −x^2 ))dx=(r/2)[(1/2)sin(2∙arcsin((x/r)))+r∙arcsin((x/r))+(π/2)]](Q5494.png)
| ||
Question and Answers Forum | ||
Question Number 5490 by 123456 last updated on 16/May/16 | ||
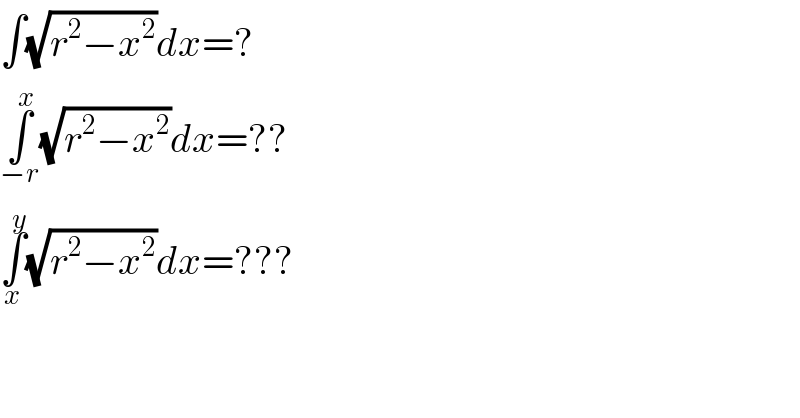 | ||
Answered by FilupSmith last updated on 16/May/16 | ||
![let x=r∙sin(θ) ⇒ dx=cos(θ)dθ ∴θ=arcsin((x/r)) ∴∫(√(r^2 −x^2 ))dx=∫((√(r^2 −r^2 sin^2 θ ))cosθ)dθ =∫cosθ(√(r^2 (1−sin^2 θ)))dθ =∫rcosθ(√(cos^2 θ))dθ =r∫cos^2 θdθ cos^2 (x)=((cos(2x)+1)/2) =r∫(1/2)(cos(2θ)+1)dθ =(r/2)((1/2)sin(2θ)+θ)+c ∴∫(√(r^2 −x^2 ))dx=(1/4)r∙sin(2∙arcsin((x/r)))+(1/2)r∙arcsin((x/r))+c −−−−−−−−−−−−−− ∫_(−r) ^x (√(r^2 −x^2 ))dx=(r/2)[(1/2)sin(2∙arcsin((x/r)))+arcsin((x/r))]_(−r) ^x =(r/2)[(1/2)sin(2∙arcsin((x/r)))+arcsin((x/r))−(1/2)sin(2∙arcsin(((−r)/r)))+r∙arcsin(((−r)/r))] =(r/2)[(1/2)sin(2∙arcsin((x/r)))+r∙arcsin((x/r))−(1/2)sin(−π)+(π/2)] ∴∫_(−r) ^x (√(r^2 −x^2 ))dx=(r/2)[(1/2)sin(2∙arcsin((x/r)))+r∙arcsin((x/r))+(π/2)]](Q5494.png) | ||
| ||