Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 151568 by tabata last updated on 21/Aug/21

$$\int \sqrt{sec\left(x\right)+tan\left(x\right)}dx$$$$$$$$howcanitsolve$$

Answered by puissant last updated on 22/Aug/21

$$=\int \sqrt{\frac{1}{cosx}+\frac{sinx}{cosx}}dx$$$$t=tan\frac{x}{2}\to dx=\frac{2}{1+t^2}dt$$$$K=\int \sqrt{\frac{1+t^2}{1-t^2}+\frac{2t}{1-t^2}}\times \frac{2}{1+t^2}dt$$$$=\int \sqrt{\frac{{(1+t)}^2}{(1-t)(1+t)}}\times \frac{2}{1+t^2}dt$$$$=2\int \sqrt{\frac{1+t}{1-t}}\times \frac{1}{1+t^2}dt$$$$u^2=\frac{1+t}{1-t}\Rightarrow u^2-u^{2}t=1+t\Rightarrow t(1+u^2)=u^2-1$$$$\Rightarrow t=\frac{u^2-1}{u^2+1}\to dt=\frac{2u(u^2+1)-2u(u^2-1)}{{(u^2+1)}^2}du$$$$\to dt=\frac{4u}{{(u^2+1)}^2}du$$$$K=2\int \frac{4u^2}{{(u^2+1)}^2}\times \frac{1}{1+{\left(\frac{u^2-1}{u^2+1}\right)}^2}du$$$$K=2\int \frac{4u^2}{{(u^2+1)}^2}\times \frac{{(u^2+1)}^2}{{(u^2+1)}^2+{(u^2-1)}^2}du$$$$K=8\int \frac{u^2}{u^4+2u^2+1+u^4-2u^2+1}du$$$$K=8\int \frac{u^2}{2(u^4+1)}du$$$$K=4\int \frac{u^2}{u^4+1}du$$$$tobecontinued...$$

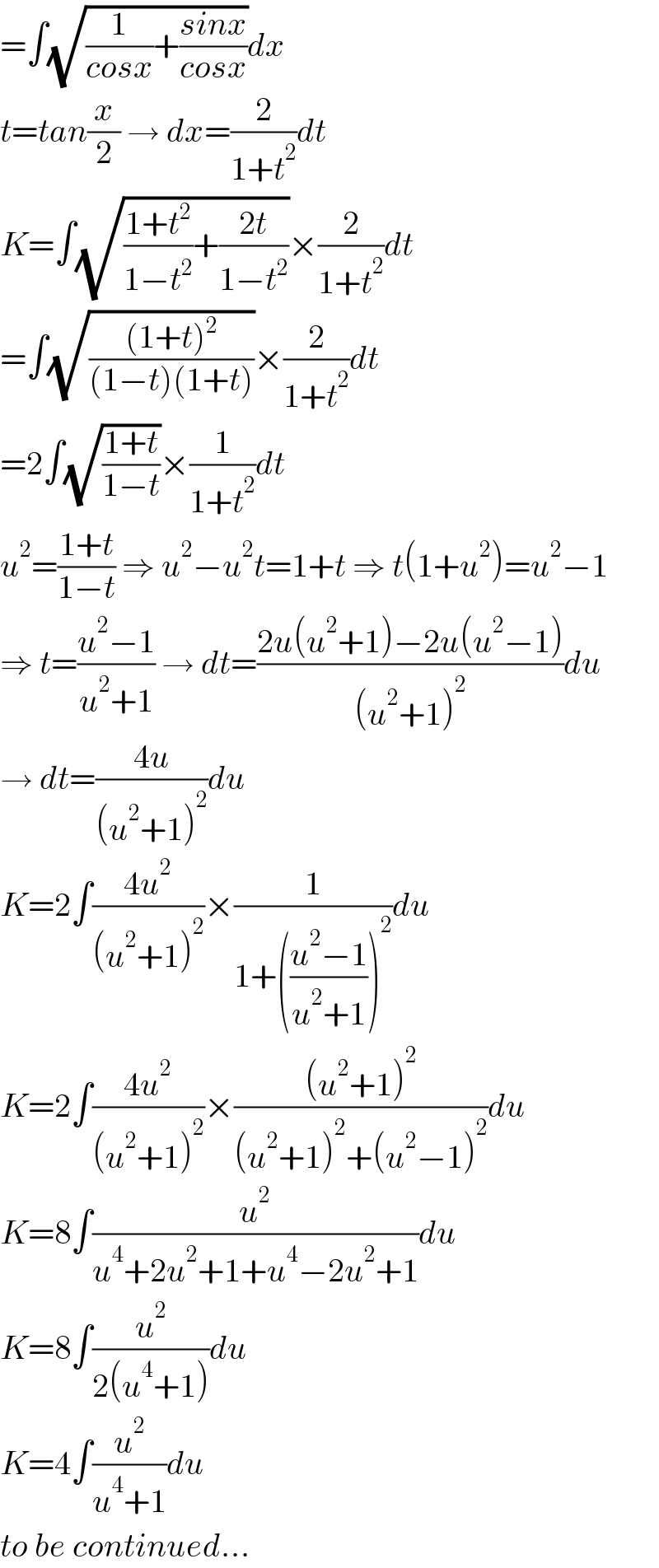
Commented by peter frank last updated on 22/Aug/21

$$4\int .\frac{1}{2}.\frac{{2\mathrm{u}}^2}{1+{\mathrm{u}}^4}=2\int \frac{{2\mathrm{u}}^2}{1+{\mathrm{u}}^4}$$$$2\int \frac{{2\mathrm{u}}^2}{1+{\mathrm{u}}^4}=4\int \frac{({\mathrm{u}}^2+1)+({\mathrm{u}}^2-1)}{1+{\mathrm{u}}^4}\mathrm{du}$$$$4[\int \frac{1+{\mathrm{u}}^2}{1+{\mathrm{u}}^4}\mathrm{du}+\int \frac{1-{\mathrm{u}}^2}{1+{\mathrm{u}}^4}\mathrm{du}]$$$$4[\int \frac{1+\frac{1}{{\mathrm{u}}^2}}{{(\mathrm{u}-\frac{1}{\mathrm{u}})}^2+2}+\int \frac{1-\frac{1}{{\mathrm{u}}^2}}{{(\mathrm{u}+\frac{1}{\mathrm{u}})}^2+2}$$$$\mathrm{t}=\mathrm{u}-\frac{1}{\mathrm{u}}$$$$\mathrm{dt}=(1+\frac{1}{{\mathrm{u}}^2})\mathrm{du}$$$$\mathrm{x}=\mathrm{u}+\frac{1}{\mathrm{u}}$$$$\mathrm{dx}=(1-\frac{1}{{\mathrm{u}}^2})\mathrm{du}$$$$4[\int \frac{1}{2}.\frac{\mathrm{dt}}{{\mathrm{t}}^2+2}+\int \frac{1}{2}.\int \frac{\mathrm{dx}}{{\mathrm{x}}^2-2}$$$$2[\frac{1}{\sqrt{2}}{\tan }^{-1}\left(\frac{\mathrm{t}}{\sqrt{2}}\right)+\frac{1}{2\sqrt{2}}\ln \left(\frac{\mathrm{x}-\sqrt{2}}{\mathrm{x}+\sqrt{2}}\right)$$$$$$

Answered by peter frank last updated on 22/Aug/21

$$\int \sqrt{\frac{1}{\cos \mathrm{x}}+\frac{\sin \mathrm{x}}{\cos \mathrm{x}}}\mathrm{dx}$$$$\int \sqrt{\frac{1+\sin \mathrm{x}}{\cos \mathrm{x}}}\mathrm{dx}$$$$\int \sqrt{\frac{{(\sin \frac{\mathrm{x}}{2}+\cos \frac{\mathrm{x}}{2})}^2}{\cos {}^2\frac{\mathrm{x}}{2}-\sin {}^2\frac{\mathrm{x}}{2}}}\mathrm{dx}$$$$\int \sqrt{\frac{{(\sin \frac{\mathrm{x}}{2}+\cos \frac{\mathrm{x}}{2})}^2}{(\cos \frac{\mathrm{x}}{2}+\sin \frac{\mathrm{x}}{2})(\cos \frac{\mathrm{x}}{2}-\sin \frac{\mathrm{x}}{2})}}\mathrm{dx}$$$$\int \sqrt{\frac{(\sin \frac{\mathrm{x}}{2}+\cos \frac{\mathrm{x}}{2})}{(\cos \frac{\mathrm{x}}{2}-\sin \frac{\mathrm{x}}{2})}}\mathrm{dx}$$$$\int \sec {}^2\frac{\mathrm{x}}{2}.\sqrt{\frac{(\tan \frac{\mathrm{x}}{2}+1)}{(1-\tan \frac{\mathrm{x}}{2})}}\mathrm{dx}$$$$\mathrm{u}=\tan \frac{\mathrm{x}}{2}$$$$\mathrm{du}=\frac{1}{2}\sec {}^2\frac{\mathrm{x}}{2}\mathrm{dx}$$$$\int \sqrt{\frac{\mathrm{u}+1}{1-\mathrm{u}}}\mathrm{du}.2$$$$\int 2\sqrt{\frac{\mathrm{u}+1}{1-\mathrm{u}}.\frac{\mathrm{u}+1}{\mathrm{u}-1}}\mathrm{du}.$$$$\int 2.\frac{\mathrm{u}+1}{\sqrt{1-{\mathrm{u}}^2}}\mathrm{du}.$$$$$$$$$$

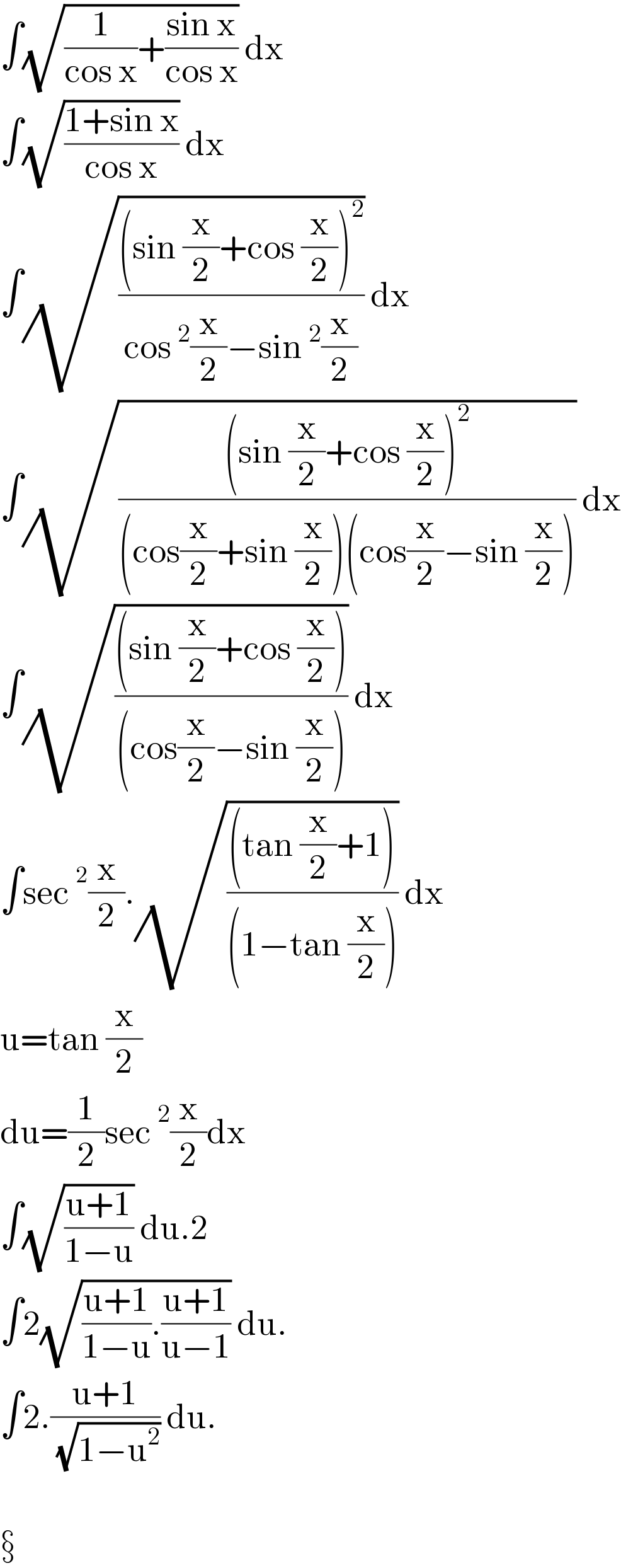
Commented by talminator2856791 last updated on 22/Aug/21

$$\mathrm{the}\mathrm{font}\mathrm{is}\mathrm{so}\mathrm{big}!\mathrm{hahahahahah}$$

Answered by MJS_new last updated on 22/Aug/21

$$\int \sqrt{\sec x+\tan x}dx=$$$$[t=\tan \frac{x}{2}\to dx=\frac{2dt}{1+t^2}]$$$$=2\int \frac{\sqrt{1+t}}{(1+t^2)\sqrt{1-t}}dt=$$$$[u=\frac{\sqrt{1-t}}{\sqrt{1+t}}\to dt=-\sqrt{(1-t){(1+t)}^3}du]$$$$=-4\int \frac{du}{u^4+1}=$$$$=\frac{1}{\sqrt{2}}\int \frac{2u-\sqrt{2}}{u^2-\sqrt{2}u+1}du-\int \frac{du}{u^2-\sqrt{2}u+1}-$$$$-\frac{1}{\sqrt{2}}\int \frac{2u+\sqrt{2}}{u^2+\sqrt{2}u+1}du-\int \frac{du}{u^2+\sqrt{2}u+1}=$$$$=\frac{\sqrt{2}}{2}\ln (u^2-\sqrt{2}u+1)-\sqrt{2}\arctan (\sqrt{2}u-1)-$$$$+\frac{\sqrt{2}}{2}\ln (u^2+\sqrt{2}u+1)-\sqrt{2}\arctan (\sqrt{2}u+1)$$$$...$$

Commented by peter frank last updated on 22/Aug/21

$$\mathrm{thank}\mathrm{you}$$

Answered by Ar Brandon last updated on 22/Aug/21

$$I=\int \sqrt{\sec x+\tan x}dx=\int \sqrt{\frac{1+\sin x}{\cos x}}dx$$$$=\int \sqrt{\frac{{(\cos \frac{x}{2}+\sin \frac{x}{2})}^2}{\cos x}}dx=\int \frac{\cos \frac{x}{2}+\sin \frac{x}{2}}{\sqrt{\cos x}}dx$$$$=\int \frac{\cos \frac{x}{2}}{\sqrt{1-{2\sin }^2\frac{x}{2}}}dx+\int \frac{\sin \frac{x}{2}}{\sqrt{{2\cos }^2\frac{x}{2}-1}}dx$$$$=\sqrt{2}\arcsin \left(\sqrt{2}\sin \frac{x}{2}\right)-\sqrt{2}\mathrm{argcosh}\left(\sqrt{2}\cos \frac{x}{2}\right)+C$$$$=\sqrt{2}\arcsin \left(\sqrt{2}\sin \frac{x}{2}\right)-\sqrt{2}\ln \mid \sqrt{2}\cos \frac{x}{2}+\sqrt{{2\cos }^2\frac{x}{2}-1}\mid +C$$

Commented by peter frank last updated on 22/Aug/21

$$\mathrm{thank}\mathrm{you}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com