
Question and Answers Forum
Question Number 82446 by M±th+et£s last updated on 21/Feb/20
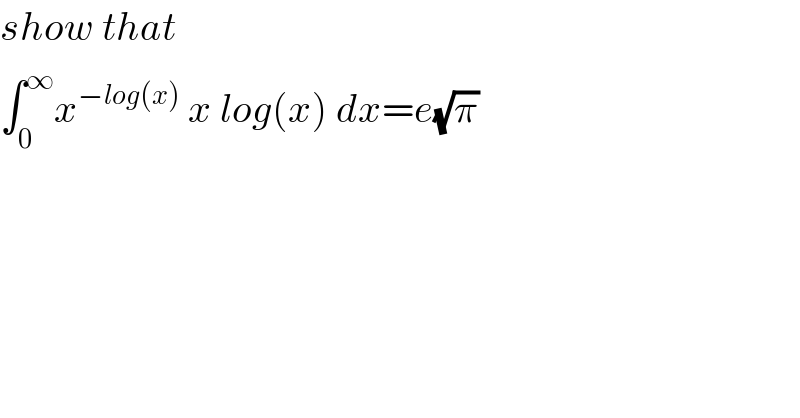
Commented by abdomathmax last updated on 21/Feb/20
![changement logx=t give x=e^t ⇒ I= ∫_(−∞) ^(+∞) (e^t )^(−t) e^t t e^t dt =∫_(−∞) ^(+∞) t e^(−t^2 +2t) dt =∫_(−∞) ^(+∞) t e^(−(t^2 −2t +1−1)) dt =∫_(−∞) ^(+∞) t e^(−(t−1)^2 +1) dt =_(t−1=u) e∫_(−∞) ^(+∞) (u+1)e^(−u^2 ) du but ∫_(−∞) ^(+∞) (u+1)e^(−u^2 ) du =∫_(−∞) ^(+∞) u e^(−u^2 ) du +∫_(−∞) ^(+∞) e^(−u^2 ) du =[−(1/2)e^(−u^2 ) ]_(−∞) ^(+∞) +(√π)=0+(√π) ⇒ I =e(√π)](Q82473.png)
Commented by M±th+et£s last updated on 21/Feb/20

Commented by mathmax by abdo last updated on 21/Feb/20
| ||
Question and Answers Forum | ||
Question Number 82446 by M±th+et£s last updated on 21/Feb/20 | ||
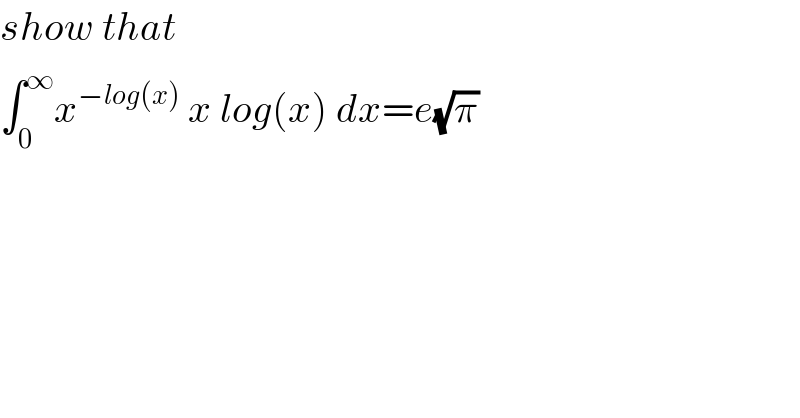 | ||
Commented by abdomathmax last updated on 21/Feb/20 | ||
![changement logx=t give x=e^t ⇒ I= ∫_(−∞) ^(+∞) (e^t )^(−t) e^t t e^t dt =∫_(−∞) ^(+∞) t e^(−t^2 +2t) dt =∫_(−∞) ^(+∞) t e^(−(t^2 −2t +1−1)) dt =∫_(−∞) ^(+∞) t e^(−(t−1)^2 +1) dt =_(t−1=u) e∫_(−∞) ^(+∞) (u+1)e^(−u^2 ) du but ∫_(−∞) ^(+∞) (u+1)e^(−u^2 ) du =∫_(−∞) ^(+∞) u e^(−u^2 ) du +∫_(−∞) ^(+∞) e^(−u^2 ) du =[−(1/2)e^(−u^2 ) ]_(−∞) ^(+∞) +(√π)=0+(√π) ⇒ I =e(√π)](Q82473.png) | ||
Commented by M±th+et£s last updated on 21/Feb/20 | ||
 | ||
Commented by mathmax by abdo last updated on 21/Feb/20 | ||
 | ||