Question and Answers Forum
Question Number 63426 by Rio Michael last updated on 04/Jul/19
![show that (a) cos[2cos^(−1) (x) +sin^(−1) (x)]= −(√(1−x^2 )) (b) ((sinα + sinβ)/(cosα−cosβ))=cot(((β−α)/2)) (c) 2cos((π/3)+p)≊ 1−(√3) if p is small enough to neglect p^2 . (d) if θ =(1/2)sin^(−1) ((3/4)), show that sinθ−cosθ = ±(1/2) (e)write tan3A in terms of tanA (f) Factorise cosθ − cos3θ−cos5θ+cos7θ (g)i) verify that f(x)=((sin2θ+sin10θ)/(cos2θ+cos10θ))=((2tan3θ)/(1−tan^2 3θ)) ii) hence find in radians the general solution of f(x)=1 sir Forkum Michael](Q63426.png)
Commented by Tony Lin last updated on 04/Jul/19
![(a) let θ=cos^(−1) (x)⇒cosθ=x let (π/2)−θ=sin^(−1) (x)⇒sinθ=(√(1−x^2 )) cos[2θ+((π/2)−θ)] =cos((π/2)+θ) =−sinθ =−(√(1−x^2 ))](Q63437.png)
Commented by Tony Lin last updated on 04/Jul/19
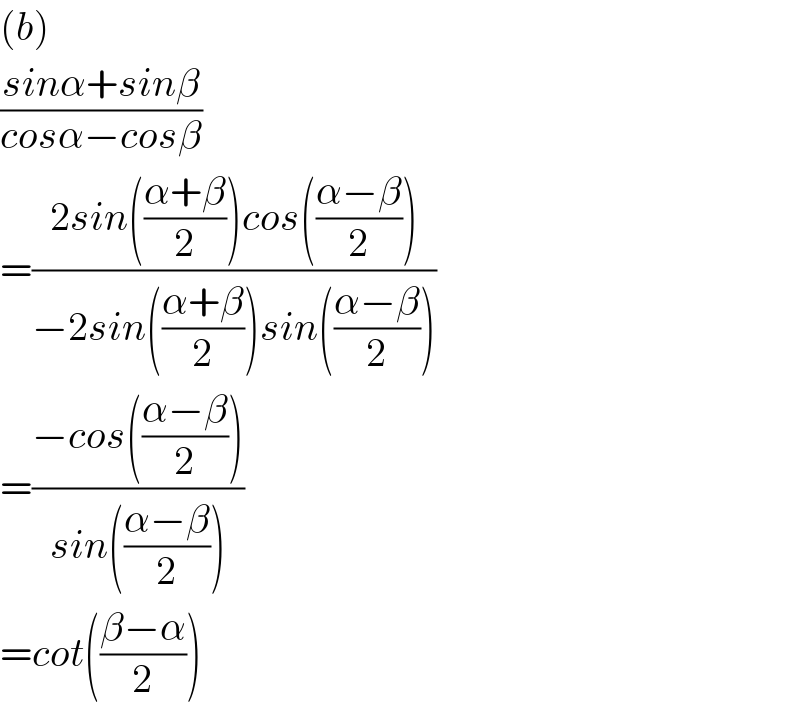
Commented by Tony Lin last updated on 04/Jul/19
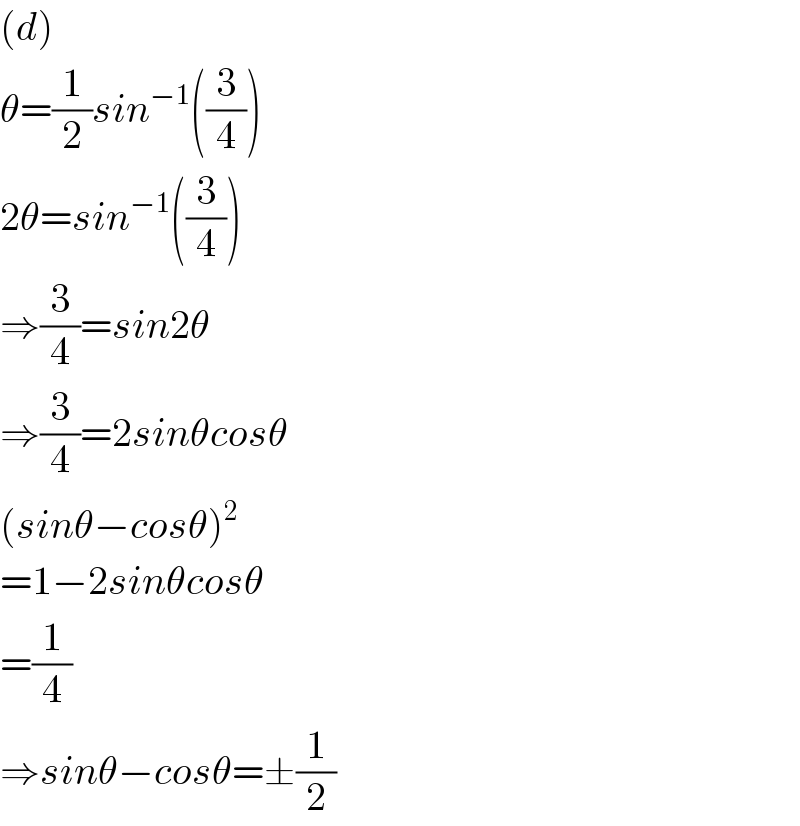
Commented by Tony Lin last updated on 04/Jul/19
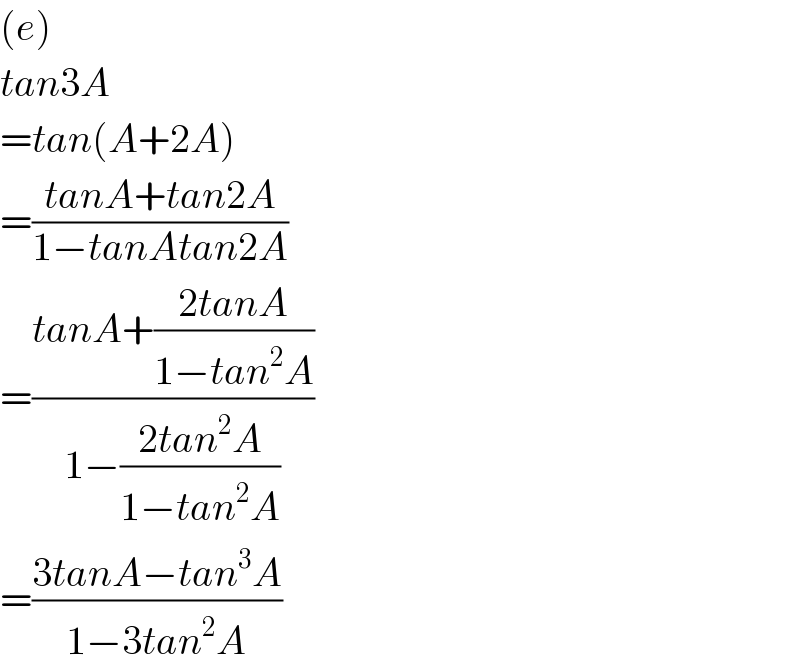
Commented by Rio Michael last updated on 05/Jul/19
Answered by som(math1967) last updated on 04/Jul/19