
Question and Answers Forum
Question Number 82041 by M±th+et£s last updated on 17/Feb/20

Commented by mr W last updated on 17/Feb/20

Commented by mr W last updated on 17/Feb/20
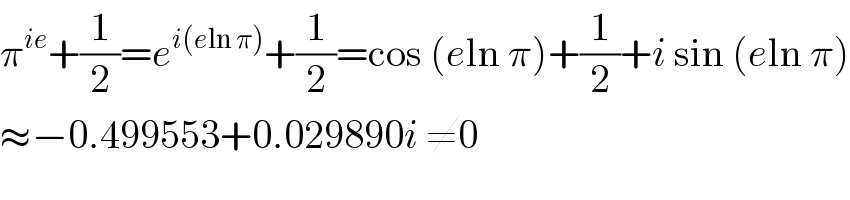
Commented by mr W last updated on 17/Feb/20
Commented by M±th+et£s last updated on 17/Feb/20

Answered by MJS last updated on 17/Feb/20
![a^(ib) = [a>0] =cos (bln a) +i sin (bln a) { (((1/2)+cos (bln a) =0)),((sin (bln a) =0)) :} { ((bln a =2k_1 π±((2π)/3); k_1 ∈Z)),((bln a =k_2 π; k_2 ∈Z)) :} ⇒ k_2 =2k_1 ±(2/3) ⇒ k_1 ∈Z xor k_2 ∈Z ⇒ no solution ⇒ ∀a∈R^+ ∀b∈R: a^(ib) +(1/2)≠0 z=cos (bln a) +i sin (bln a) ⇒ abs z =1∧arg z =bln a ⇒ π^(ie) =e^(ie ln π) ≈−.999553+.0298898i ⇒ π^(ie) +(1/2)≠0](Q82049.png)
