simplify S_n (x) =Σ_(k=0) ^n C_n ^k cos^4 (πkx) 2) calculate I_n =∫_0 ^(1/3) S


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 67373 by mathmax by abdo last updated on 26/Aug/19

$s i m p l i f y S_{n} (x) = \sum_{k = 0}^{n} C_{n}^{k} {c o s}^{4} (π k x)$ $2) c a l c u l a t e I_{n} = \int_{0}^{\frac{1}{3}} S_{n} (x) d x$
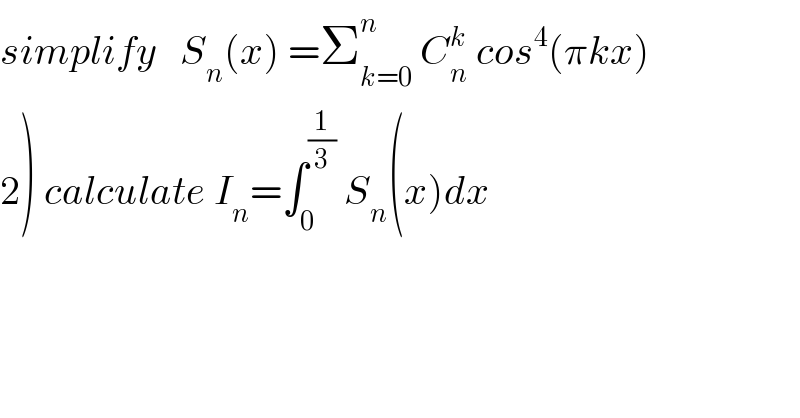
Commented by ~ À ® @ 237 ~ last updated on 27/Aug/19

$L e t s t a t e T_{n} = \underset{k = 0}{\sum^{n}} C_{n}^{k} {s i n}^{4} (π k x)$ $k n o w i n g t h a t {c o s}^{4} t + {s i n}^{4} t = 1 - \frac{{s i n}^{2} 2 t}{2} = \frac{3 + c o s 4 t}{4} a n d {c o s}^{2} t - {s i n}^{2} t = c o s 2 t$ $S_{n} + T_{n} = \frac{3}{4} \underset{k = 0}{\sum^{n}} C_{n}^{k} + \frac{1}{4} \underset{k = 0}{\sum^{n}} C_{n}^{k} c o s (4 π k x) = 3 . 2^{n - 2} + \frac{1}{4} R e (\underset{k = 0}{\sum^{n}} C_{n}^{k} {(e^{i 4 π x})}^{k}) = 3 . 2^{n - 2} + \frac{1}{4} R e [{(1 + e^{i 4 π x})}^{n}]$ $= 3 . 2^{n - 2} + \frac{1}{4} R e [e^{i 2 π n x} {(e^{i 2 π x} + e^{- i 2 π x})}^{n}] = 3 . 2^{n - 2} + 2^{n - 2} c o s (2 π n x) (c o s {(2 π x)}^{n}$ $S_{n} - T_{n} = \underset{k = 0}{\sum^{n}} C_{n}^{k} c o s (2 π k x) = R e [{(1 + e^{i 2 π x})}^{n}] = 2^{n} c o s (n π x) {(c o s (π x))}^{n}$ $N o w w e c a n d e d u c e$ $S_{n} = 2^{n - 3} [3 + c o s (2 π n x) {(c o s (2 π x))}^{n} + 4 c o s (n π x) {(c o s (π x))}^{n}]$ $B u t i f w e a r e s e a r c h i n g a l o w e s t f o r m i n t h e w a y t o f i n d I$ $w e c a n u s e {c o s}^{4} t = \frac{3 + c o s 4 t}{8} + \frac{c o s 2 t}{2}$ $I_{n} = \frac{1}{3} + \underset{k = 1}{\sum^{n}} C_{n}^{k} \int_{0}^{\frac{1}{3}} [\frac{3}{8} + \frac{c o s (4 π k x)}{8} + \frac{c o s (2 π k x)}{2}] d x$ $= \frac{1}{3} + \underset{k = 1}{\sum^{n}} C_{n}^{k} {[\frac{3 x}{8} + \frac{s i n (4 π k x)}{32 π k} + \frac{s i n (2 π k x)}{4 π k}]}_{0}^{\frac{1}{3}}$ $= (\frac{1}{3} - \frac{1}{8}) + \frac{1}{8} \underset{k = 0}{\sum^{n}} C_{n}^{k} + \frac{1}{32 π} \underset{k = 1}{\sum^{n}} C_{n}^{k} \frac{s i n (\frac{4 π k}{3})}{k} + \frac{1}{4 π} \underset{k = 1}{\sum^{n}} C_{n}^{k} \frac{s i n (\frac{2 π k}{3})}{k}$
Commented by mathmax by abdo last updated on 27/Aug/19

$t h a n k y o u s i r .$
Commented by mathmax by abdo last updated on 27/Aug/19
$1) we have cos^4 u =(((1+cos(2u)/2))^2 =(1/4)(1+2cos(2u)+((1+cos(4u))/2)) =(1/8){2+4cos(2u) +1+cos(4u)} =(1/8){3 +4cos(2u)+cos(4u)} =(3/8) +(1/2)cos(2u)+(1/8)cos(4u) ⇒ S_n =Σ_(k=0) ^n C_n ^k {(3/8)+(1/2)cos(2πkx)+(1/8)cos(4πkx)} =(3/8)×2^n +(1/2) Σ_(k=0) ^n C_n ^k cos(2πkx) +(1/8)Σ_(k=0) ^n C_n ^k cos(4πkx)} Σ_(k=0) ^n C_n ^k cos(2πkx) =Re(Σ_(k=0) ^n C_n ^k e^(i2πkx) ) and Σ_(k=0) ^n C_n ^k (e^(i2πx) )^k =(1+e^(i2πx) )^n =(1+cos(2πx)+isin(2πx))^n ∣1+cos(2πx)+isin(2πx)∣ =(√((1+cos(2πx))^2 + sin^2 (2πx))) =(√(1+2cos(2πx)+1))=(√(2+2cos(2πx)))=(√2)(√(2cos^2 (πx))) =2∣cos(πx)∣ ⇒ 1+cos(2πx)+isin(2πx) =2∣cos(πx)∣ e^(i arctan(((sin(2πx))/(1+cos(2πx))))) =2∣cos(πx)∣e^(iπx) because ((sin(2πx))/(1+cos(2πx))) =((2sin(πx)cos(πx))/(2cos^2 (πx))) =tan(πx) ⇒ (1+cos(2πx)+isin(2πx))^n =2^n ∣cos(πx)∣^n e^(inπx) also we have ⇒Σ_(k=0) ^(n ) C_n ^k cos(2πkx) =2^n ∣cos(πx)∣^n cos(nπx) also Σ_(k=0) ^n C_n ^k cos(4πkx) =2^n ∣cos(2πx)∣^n cos(2nπx) ⇒ S_n =((3×2^n )/8) + 2^(n−1) ∣cos(πx)∣^n cos(nπx) +2^(n−3) ∣cos(2πx)∣^n cos(2nπx)$
$1) w e h a v e {c o s}^{4} u = {(\frac{1 + c o s (2 u}{2})}^{2} = \frac{1}{4} (1 + 2 c o s (2 u) + \frac{1 + c o s (4 u)}{2})$ $= \frac{1}{8} {2 + 4 c o s (2 u) + 1 + c o s (4 u)} = \frac{1}{8} {3 + 4 c o s (2 u) + c o s (4 u)}$ $= \frac{3}{8} + \frac{1}{2} c o s (2 u) + \frac{1}{8} c o s (4 u) \Rightarrow$ $S_{n} = \sum_{k = 0}^{n} C_{n}^{k} {\frac{3}{8} + \frac{1}{2} c o s (2 π k x) + \frac{1}{8} c o s (4 π k x)}$ $= \frac{3}{8} \times 2^{n} + \frac{1}{2} \sum_{k = 0}^{n} C_{n}^{k} c o s (2 π k x) + \frac{1}{8} \sum_{k = 0}^{n} C_{n}^{k} c o s (4 π k x)}$ $\sum_{k = 0}^{n} C_{n}^{k} c o s (2 π k x) = R e (\sum_{k = 0}^{n} C_{n}^{k} e^{i 2 π k x}) a n d$ $\sum_{k = 0}^{n} C_{n}^{k} {(e^{i 2 π x})}^{k} = {(1 + e^{i 2 π x})}^{n} = {(1 + c o s (2 π x) + i s i n (2 π x))}^{n}$ $∣ 1 + c o s (2 π x) + i s i n (2 π x) ∣ = \sqrt{{(1 + c o s (2 π x))}^{2} + {s i n}^{2} (2 π x)}$ $= \sqrt{1 + 2 c o s (2 π x) + 1} = \sqrt{2 + 2 c o s (2 π x)} = \sqrt{2} \sqrt{2 {c o s}^{2} (π x)}$ $= 2 ∣ c o s (π x) ∣ \Rightarrow$ $1 + c o s (2 π x) + i s i n (2 π x) = 2 ∣ c o s (π x) ∣ e^{i a r c t a n (\frac{s i n (2 π x)}{1 + c o s (2 π x)})} = 2 ∣ c o s (π x) ∣ e^{i π x} b e c a u s e$ $\frac{s i n (2 π x)}{1 + c o s (2 π x)} = \frac{2 s i n (π x) c o s (π x)}{2 {c o s}^{2} (π x)} = t a n (π x) \Rightarrow$ ${(1 + c o s (2 π x) + i s i n (2 π x))}^{n} = 2^{n} ∣ c o s (π x) ∣^{n} e^{i n π x} a l s o w e h a v e$ $\Rightarrow \sum_{k = 0}^{n} C_{n}^{k} c o s (2 π k x) = 2^{n} ∣ c o s (π x) ∣^{n} c o s (n π x) a l s o$ $\sum_{k = 0}^{n} C_{n}^{k} c o s (4 π k x) = 2^{n} ∣ c o s (2 π x) ∣^{n} c o s (2 n π x) \Rightarrow$ $S_{n} = \frac{3 \times 2^{n}}{8} + 2^{n - 1} ∣ c o s (π x) ∣^{n} c o s (n π x) + 2^{n - 3} ∣ c o s (2 π x) ∣^{n} c o s (2 n π x)$
Commented by mathmax by abdo last updated on 27/Aug/19
$2) ∫_0 ^(1/3) S(x)dx =∫_0 ^(1/3) {(3/8)2^n +(1/2)Σ_(k=0) ^n C_n ^k cos(2πkx)+(1/8)Σ_(k=0) ^n C_n ^k cos(4πkx)}dx =2^(n−3) +(1/2)Σ_(k=0) ^n ∫_0 ^(1/3) cos(2πkx)dx +(1/8)Σ_(k=0) ^n C_n ^k ∫_0 ^(1/3) cos(4πkx)dx =2^(n−3) +(1/2)Σ_(k=0) ^n (1/(2πk))[sin(2πkx]_0 ^(1/3) +(1/8)Σ_(k=0) ^n C_n ^k (1/(4πk))[sin(4πkx)]_0 ^(1/3) =2^(n−3) + (1/(4π)) Σ_(k=0) ^n ((sin(((2πk)/3)))/k) +(1/(32π))Σ_(k=0) ^n C_n ^k ((sin(((4πk)/3)))/k) .$
$2) \int_{0}^{\frac{1}{3}} S (x) d x = \int_{0}^{\frac{1}{3}} {\frac{3}{8} 2^{n} + \frac{1}{2} \sum_{k = 0}^{n} C_{n}^{k} c o s (2 π k x) + \frac{1}{8} \sum_{k = 0}^{n} C_{n}^{k} c o s (4 π k x)} d x$ $= 2^{n - 3} + \frac{1}{2} \sum_{k = 0}^{n} \int_{0}^{\frac{1}{3}} c o s (2 π k x) d x + \frac{1}{8} \sum_{k = 0}^{n} C_{n}^{k} \int_{0}^{\frac{1}{3}} c o s (4 π k x) d x$ $= 2^{n - 3} + \frac{1}{2} \sum_{k = 0}^{n} \frac{1}{2 π k} [s i n {(2 π k x]}_{0}^{\frac{1}{3}} + \frac{1}{8} \sum_{k = 0}^{n} C_{n}^{k} \frac{1}{4 π k} {[s i n (4 π k x)]}_{0}^{\frac{1}{3}}$ $= 2^{n - 3} + \frac{1}{4 π} \sum_{k = 0}^{n} \frac{s i n (\frac{2 π k}{3})}{k} + \frac{1}{32 π} \sum_{k = 0}^{n} C_{n}^{k} \frac{s i n (\frac{4 π k}{3})}{k} .$
	Answered by Smail last updated on 27/Aug/19

	${c o s}^{4} (k π x) = \frac{1}{4} {(1 + c o s (2 k π x))}^{2}$ $= \frac{1}{4} (1 + {c o s}^{2} (2 k π x) + 2 c o s (2 k π x))$ $= \frac{1}{8} (2 + 1 + c o s (4 k π x) + 4 c o s (2 k π x))$ $S o, S_{n} (x) = \frac{1}{8} \underset{k = 0}{\sum^{n}} C_{n}^{k} (3 + c o s (4 k π x) + 4 c o s (2 k π x))$ $= \frac{1}{8} (3 \underset{k = 0}{\sum^{n}} C_{n}^{k} + \underset{k = 0}{\sum^{n}} C_{n}^{k} c o s (4 k π x) + 4 \underset{k = 0}{\sum^{n}} C_{n}^{k} c o s (2 k π x))$ $= \frac{1}{8} (3 \times 2^{n} + R e (\underset{k = 0}{\sum^{n}} C_{n}^{k} e^{4 i k π x}) + 4 R e (\underset{k = 0}{\sum^{n}} C_{n}^{k} e^{2 i k π x}))$ $= \frac{1}{8} (3 \times 2^{n} + R e ({(1 + e^{4 i π x})}^{n}) + 4 R e ({(1 + e^{2 i π x})}^{n}))$ $= \frac{1}{8} (3 \times 2^{n} + R e ({(1 + c o s (4 π x) + i s i n (4 π x))}^{n}) + 4 R e ({(1 + c o s (2 π x) + i s i n (2 π x))}^{n}))$ $= \frac{1}{8} (3 \times 2^{n} + R e ({(2 c o s (2 π x) e^{2 i π x})}^{n}) + 4 R e ({(2 c o s (π x) e^{i π x})}^{n}))$ $= \frac{1}{8} (3 \times 2^{n} + R e (2^{n} {c o s}^{n} (2 π x) e^{2 i n π x}) + 4 R e ((2^{n} {c o s}^{n} (π x) e^{i n π x}))$ $= \frac{2^{n}}{8} (3 + {c o s}^{n} (2 π x) c o s (2 n π x) + 4 {c o s}^{n} (π x) c o s (n π x))$ $\underset{k = 0}{\sum^{n}} C_{n}^{k} {c o s}^{4} (k π x) = 2^{n - 3} (3 + {c o s}^{n} (2 π x) c o s (2 n π x) + 4 {c o s}^{n} (π x) c o s (n π x))$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum