Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 167312 by cortano1 last updated on 12/Mar/22

$$\int \frac{\sin {}^3\mathrm{x}+1}{\sin {}^2\mathrm{x}-1}\mathrm{dx}=?$$

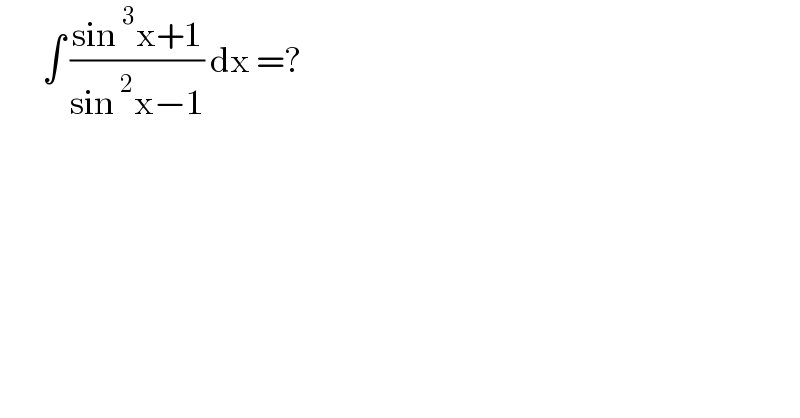
Commented by Florian last updated on 10/Apr/22

$$Simplify:\frac{{sin}^{3}x+1}{{sin}^2-1}=\frac{{sin}^2\left(x\right)-sin\left(x\right)+1}{sin\left(x\right)-1}$$$$=\int \frac{{sin}^2\left(x\right)}{sin\left(x\right)-1}dx-\int \frac{sin\left(x\right)}{sin\left(x\right)-1}dx+\int \frac{1}{sin\left(x\right)-1}dx$$$$\int \frac{{sin}^2\left(x\right)}{sin\left(x\right)-1}dx=\frac{2}{tan\left(\frac{x}{2}\right)-1}-cos\left(x\right)+x$$$$\int \frac{sin\left(x\right)}{sin\left(x\right)-1}dx=-4(-\frac{1}{2(tan\left(\frac{x}{2}\right)-1)}-\frac{1}{2}arctan\left(tan\left(\frac{x}{2}\right)\right))$$$$\int \frac{1}{sin\left(x\right)-1}dx=2(\frac{1}{{(-1+tan\left(\frac{x}{2}\right))}^2}+\frac{2}{-1+tan\left(\frac{x}{2}\right)}+\frac{tan\left(\frac{x}{2}\right)}{2tan\left(\frac{x}{2}\right)+{sec}^2\left(\frac{x}{2}\right)})$$$$=x+\frac{4}{tan\left(\frac{x}{2}\right)-1}-cos\left(x\right)-2arctan\left(tan\left(\frac{x}{2}\right)\right)+\frac{2}{{(tan\left(\frac{x}{2}\right)-1)}^2}+\frac{2tan\left(\frac{x}{2}\right)}{2tan\left(\frac{x}{2}\right)-{sec}^2\left(\frac{x}{2}\right)}+c,c\in R$$

Answered by MJS_new last updated on 12/Mar/22

$$-\int \frac{1+{\sin }^{3}x}{1-{\sin }^{2}x}dx=\int (\sin x-\frac{1}{1-\sin x})dx=$$$$=-\cos x-\frac{\cos x}{1-\sin x}+C$$

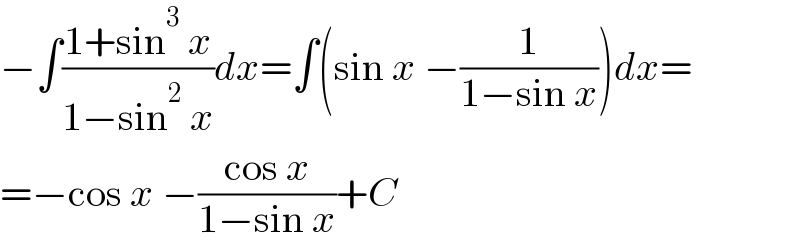
Commented by cortano1 last updated on 13/Mar/22

$$=-\cos \mathrm{x}-\frac{\cos \mathrm{x}(1+\sin \mathrm{x})}{\cos {}^2\mathrm{x}}+\mathrm{c}$$$$=-\cos \mathrm{x}-\sec \mathrm{x}-\tan \mathrm{x}+\mathrm{c}$$

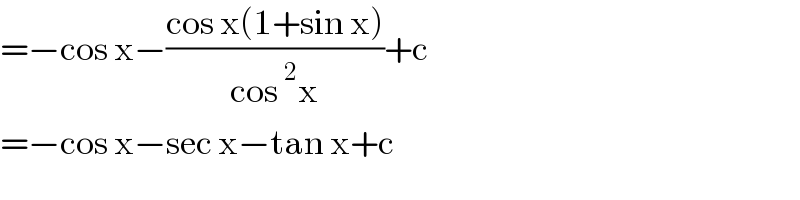
Answered by LEKOUMA last updated on 13/Mar/22

$$=\int \frac{(\sin x+1)(\sin {}^{2}x-\sin x+1)}{(\sin x-1)(\sin x+1)}dx$$$$=\int \frac{\sin {}^{2}x-\sin x+1}{\sin x-1}dx$$$$=\int \frac{\sin {}^{2}x-\sin x}{\sin x-1}dx+\int \frac{1}{\sin x-1}dx$$$$=\int \frac{\sin x(\sin x-1)}{(\sin x-1)}dx+\int \frac{1}{\sin x-1}dx$$$$=\int \sin xdx+\int \frac{1}{\sin x-1}dx$$$$=-\cos x+\int \frac{1}{\sin x-1}dx$$$$\int \frac{1}{\sin x-1}dx$$$$\sin x=\frac{2\tan \left(\frac{x}{2}\right)}{1+{\tan }^2\left(\frac{x}{2}\right)}$$$$\int \frac{1}{\frac{2\tan \left(\frac{x}{2}\right)}{1+\tan {}^2\left(\frac{x}{2}\right)}-1}dx$$$$lett=\tan \left(\frac{x}{2}\right)\Rightarrow dt=\frac{1}{2}(1+\tan {}^2\left(\frac{x}{2}\right))dx$$$$\int \frac{1}{\frac{2t}{1+t^2}-1}\times \frac{dt}{\frac{1}{2}(1+t^2)}$$$$\int \frac{1}{\frac{2t-1-t^2}{1+t^2}}\times \frac{dt}{\frac{1}{2}(1+t^2)}$$$$\int \frac{1+t^2}{2t-1-t^2}\times \frac{dt}{\frac{1}{2}(1+t^2)}$$$$\frac{1}{2}\int \frac{1}{2t-1-t^2}dt=\frac{1}{2}\int \frac{1}{-t^2+2t-1}dt$$$$\frac{1}{2}\int \frac{1}{-t^2+2t-1}dt=-\frac{1}{2}\int \frac{1}{t^2-2t+1}dt$$$$-\frac{1}{2}\int \frac{1}{{(t-1)}^2+\frac{3}{4}}dt$$$$letu=t-1\Rightarrow du=dt$$$$-\frac{1}{2}\int \frac{1}{u^2+\frac{3}{4}}du=-\frac{1}{2}\int \frac{1}{u^2+{\left(\frac{\sqrt{3}}{2}\right)}^2}du$$$$=-\frac{1}{2}\frac{1}{\frac{\sqrt{3}}{2}}{\tan }^{-1}\left(\frac{u}{\frac{\sqrt{3}}{2}}\right)+c,c\in lR$$$$=-\sqrt{3}{\tan }^{-1}\left(\frac{2u}{\sqrt{3}}\right)+c,c\in R$$$$=-\sqrt{3}{\tan }^{-1}\left(\frac{2\sqrt{3}}{3}u\right)+c,c\in lR$$$$=-\sqrt{3}{\tan }^{-1}\left[\frac{2\sqrt{3}}{3}(t-1)\right]+c,c\in R$$$$=\sqrt{3}{\tan }^{-1}\left[\frac{2\sqrt{3}}{3}(\tan \left(\frac{x}{2}\right)-1)\right]+c,c\in lR$$$$\int \frac{1}{\sin x-1}dx=\sqrt{3}{\tan }^{-1}\left[\frac{2\sqrt{3}}{3}(\tan \left(\frac{x}{2}\right)-1)\right]+c,c\in lR$$$$=-\cos x+\sqrt{3}{\tan }^{-1}\left[\frac{2\sqrt{3}}{3}(\tan \left(\frac{x}{2}\right)-1)\right]+c,c\in lR$$$$\int \frac{\sin {}^{3}x+1}{\sin {}^{2}x-1}dx=-\cos x+\sqrt{3}{\tan }^{-1}\left[\frac{2\sqrt{3}}{3}(\tan \left(\frac{x}{2}\right)-1)\right]+c,c\in lR$$$$Proposition$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com